机器学习“傻瓜式”理解(3)KNN算法(初步理解)
面对这个算法需要蹦出来几个问题:KNN是什么?可以解决什么问题?怎么实现?有什么优缺点?
首先,KNN我们通常称之为K近邻算法,通俗的理解便是如果我们认为两个特征之间他们足够相似,我们就有理由认为他们属于同一个类别。
丰富上一小节的一张图以后:
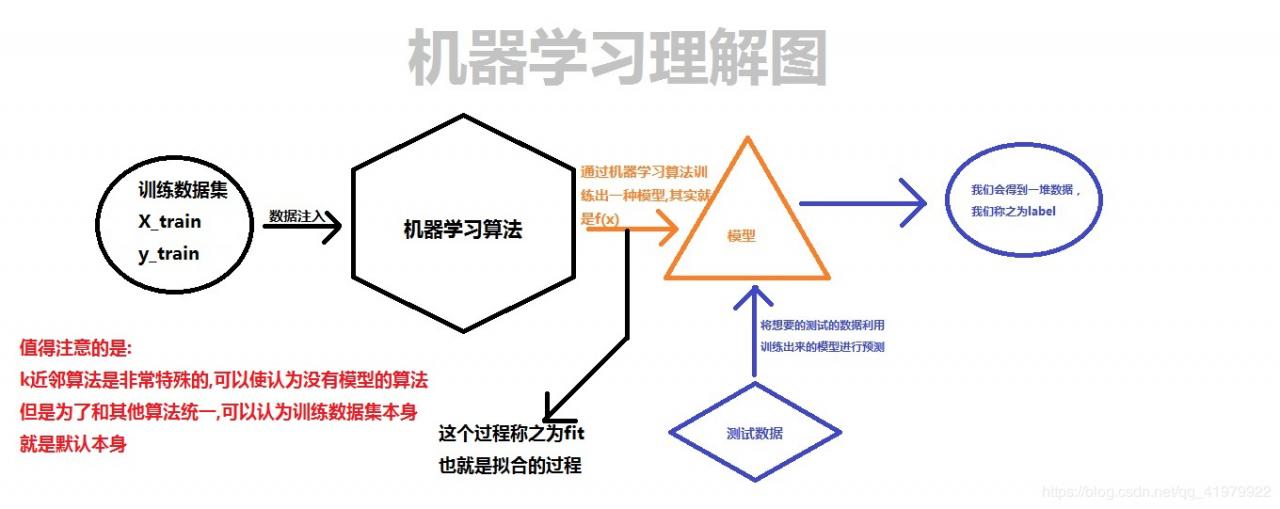
接着,通常情况下我们使用KNN是用来解决分类问题,当然,很少情况下我们也会使用它来解决回归问题。
其主要的解决思路为:
①求出我们需要预测的点与数据集中的点之间的距离,根据初中所学,我们使用欧拉距离来表示。
②将距离进行排序,找前k个中出现次数最多的便是我们的预测结果。

代码实现:(Github处于外网,所以我在这里直接贴上自己封装的KNN算法)
源码在源码中
import numpy as np
from collections import Counter
from math import sqrt
class KNeighborsClassifier:
def __init__(self,k):
'''check'''
assert k>=1,"K must be valid"
self.k = k
'''private'''
self._X_train = None
self._y_train = None
def fit(self,X,y):
'''check'''
assert X.shape[0] == y.shape[0],\
"The data size must be valid"
assert self.k <= y.shape[0],\
"K must be valid"
self._X_train = X
self._y_train = y
'''according to the scikit-learn,we need to return self'''
return self
def predict(self,x_predict):
'''check'''
assert self._X_train.shape[1] == x_predict.shape[1],\
"The size must be valid"
assert self._X_train is not None and self._y_train is not None,\
"The process fit should do before predict"
y_predict = [self._doPredict(x) for x in x_predict]
return y_predict
def _doPredict(self,x):
'''check'''
assert x.shape[1] == self._X_train.shape[1],\
"The size must be valid"
distances = [sqrt(np.sum((x - self._X_train)**2)) for x_train in self._X_train]
sortedIndex = np.argsort(distances)
topK = [self._y_train[i] for i in sortedIndex[:self.k]]
return Counter(topK).most_common(1)[0][0]
def __repr__(self):
return "KNeighborsClassifier()"
1.准备初始数据,并通过matplotlib工具查看图像
import numpy as np
import matplotlib.pyplot as plt
from myML.Knn import KNeighborsClassifier
raw_x = [[3.3935, 2.3312],
[3.1101, 1.7815],
[1.3438, 3.3684],
[3.5823, 4.6792],
[2.2804, 2.8670],
[7.4234, 4.6965],
[5.7451, 3.5340],
[9.1722, 2.5111],
[7.7928, 3.4241],
[7.9398, 0.7916]]
raw_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
X_train = np.array(raw_x)
y_train = np.array(raw_y)
plt.scatter(X_train[y_train==0,0],X_train[y_train==0,1],color='red')
plt.scatter(X_train[y_train==1,0],X_train[y_train==1,1],color='blue')
plt.show()
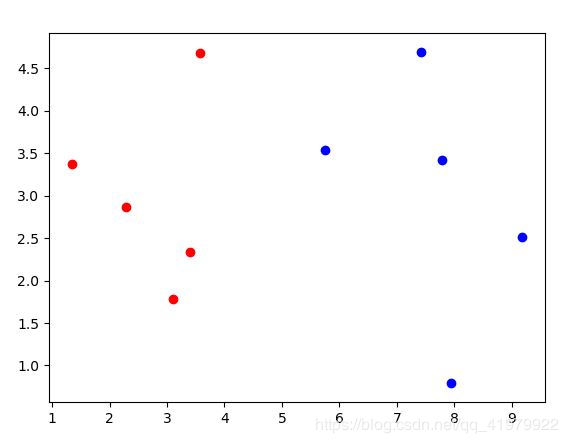
添加点进行预测
#假设下点为所要预测的点
x = np.array([8.0936, 3.3657])
plt.scatter(x[0],x[1],color='green')
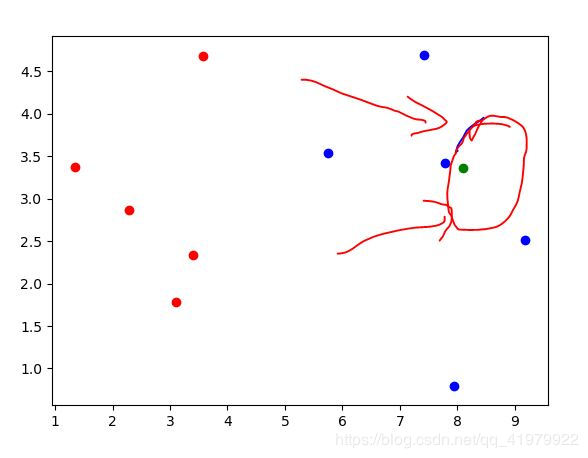
通过上图看到,绿色的点为所有预测的点,眼睛直观看来,绿色应该是和蓝色点一个类别。通过使用我们的算法代码预测后:
#假设下点为所要预测的点
x = np.array([8.0936, 3.3657]).reshape(1,-1)
Knn_cif = KNeighborsClassifier(k = 5)
Knn_cif.fit(X_train,y_train)
result = Knn_cif.predict(x)
if result[0] == 1:
print("Green")
else:
print("Red")
# 打印结果为Green,结果预测准确
KNN优缺点
优点:
1.KNN算法不需要训练过程,也可理解为这个算法没有模型或者模型就是数据本身
2.对数学要求少,效果较好。
3.完整的刻画机器学习的过程,既可以解决分类问题也可以解决回归问题,而且可以天然的解决多分类问题。
缺点:
1.运行效率极低,并且高度依赖数据,这在机器学习算法中不可取。如果我们本身的数据产生错误,例如在三近邻算法中,有两个数据出错,预测结果就极其容易出错。
2.通过KNN算法我们得到的预测结果具有不可解释性。按照KNN算法的实现逻辑,为什么离预测点最近的就是它的类型,我们拿到结果后还需要更多的东西,KNN提供不了。
3.维数灾难。我们上面所呈现的例子是二维,如果在多维空间下,两个点之间的欧拉距离十分大,容易造成维数灾难。
from sklearn.neighbors import KNeighborsClassifier
sklearnKnn = KNeighborsClassifier(n_neighbors = 5)
sklearnKnn.fit(X_train,y_train)
sklearnKnn.predict(x)
小提示:通过我们自己的封装以及scikit-learn的调用可以发现,我们在进行机器学习的过程中常常按照实例化->fit->predict的过程来进行预测。
作者:崔振凯