集成学习(三)—— Adaboost的理念和推导
adaboost也是集成学习的一种,也是很多模型一起做决策,最终投票决定,下面会介绍一下adaboost的理念、流程以及简要推导。
理念 1.错题应该被多做bagging中的抽样是随机的,但更boosting的策略是使那些被分错类的数据以更高的概率出现,简单来说,在平时练习的过程中应该多做错题,这样真正考试的时候才更有把握。
2.强者拥有更多的话语权我们有很多的分类器,有的分类器厉害一点,正确率高。那么相应的在最终投票的时候,不应该是简单的一人一票,而是强的分类器拥有更多的票数。换句话说,好的分类器的权重应该更大。
3.强者做错的题更加重要同样是错题,做错的原因可能是这题真的难,但也可能是做题者太菜。因此如果一个很强的人都做错了这题,才能证明这题是真的难。故我们在提升错题下一次的出现概率时,同时也要考虑做题者本身的能力问题。
推导分类器的权重用α\alphaα表示,数据的权重用www表示,弱分类器用h(x)h(x)h(x)表示,真实值用yyy表示,最终的分类器用H(x)H(x)H(x)表示。
数据分为两类:+1和-1。
我们定义这样定义最终的分类器:
H(x)=∑t=1Tαt⋅h(x)t
H(x)=\sum_{t=1}^T\alpha_t\cdot h(x)_t
H(x)=t=1∑Tαt⋅h(x)t
虽然我们现在还不知道到α\alphaα的具体值,但是没关系,只要知道它代表了一个分类器的重要性就可以了。显然α\alphaα一定和这个分类器的正确率正相关,但也远不止这么简单,我们后面会推导,别急。
根据我们上面的理念第二条和第三条:错题应该被多做和强者做错的题更加重要。可以这样定义下一次数据的权重分布:
wi+1=wiZ⋅exp{−αih(x)iy}
w_{i+1}=\frac{w_i}{Z}\cdot exp\{-\alpha_ih(x)_iy\}
wi+1=Zwi⋅exp{−αih(x)iy}
其中Z是一个归一化的操作,Z=∑w⋅exp{−αih(x)y}Z=\sum w\cdot exp\{-\alpha_ih(x)y\}Z=∑w⋅exp{−αih(x)y},这样一来就保证了在下一轮的数据权重之和为1。
我们主要来看wi⋅exp{−αih(x)iy}w_i\cdot exp\{-\alpha_ih(x)_iy\}wi⋅exp{−αih(x)iy}这部分,有两种情况,预测对了和预测错了。
如果预测对了,则h(x)y为1,−αih(x)iy-\alpha_ih(x)_iy−αih(x)iy就一定小于0,也就是说会使exp{−αih(x)iy}exp\{-\alpha_ih(x)_iy\}exp{−αih(x)iy}处于0~1之间,就减少了预测正确数据的出现概率;
反之如果预测错了,则h(x)y为-1,−αih(x)iy-\alpha_ih(x)_iy−αih(x)iy就一定大于0,也就是说会使exp{−αih(x)iy}exp\{-\alpha_ih(x)_iy\}exp{−αih(x)iy}大于1,就增大了预测错误数据的出现概率;
同时增大或减小的幅度由分类器本事的重要性来决定,越重要的分类器比重越大。
下面看一下α\alphaα的推导:
最终分类器损失函数可以这样定义:
J=exp{−H(x)y}=exp{−αh(x)y}
J = exp\{-H(x)y\} = exp\{-\alpha h(x)y\}
J=exp{−H(x)y}=exp{−αh(x)y}
也就是说预测正确时,指数部分为负数;预测错误时指数部分为正数。预测正确的越多可以使得J更小,因此这个损失函数的定义是合理的。
我们假定α\alphaα与轮数无关,仅与本次训练有关,则可将上式推广到单轮训练(即将α\alphaα和h(x)h(x)h(x)都降了训练轮数那一维)。
则有下式:
J=e−α(预测正确数量)+eα(预测错误数量)
J = e^{-\alpha}(预测正确数量) + e^\alpha(预测错误数量)
J=e−α(预测正确数量)+eα(预测错误数量)
e−αe^{-\alpha}e−α是代表预测正确的部分,即h(x)y得1;eαe^{\alpha}eα是代表预测错误的部分,即h(x)y得-1;
设错误率为ϵ\epsilonϵ,则正确与错误的比为1−ϵ:ϵ1-\epsilon:\epsilon1−ϵ:ϵ,损失函数可改写为:
J=e−α(1−ϵ)+eαϵ
J = e^{-\alpha}(1-\epsilon) + e^\alpha \epsilon
J=e−α(1−ϵ)+eαϵ
对α\alphaα求导可得
∂J∂α=−e−α(1−ϵ)+eαϵ
\frac{\partial J}{\partial \alpha}= -e^{-\alpha}(1-\epsilon) + e^\alpha \epsilon
∂α∂J=−e−α(1−ϵ)+eαϵ
令其为0可得
α=kln1−ϵϵ
\alpha = kln\frac{1-\epsilon}\epsilon
α=klnϵ1−ϵ
一般k都取0.5,即
α=12ln1−ϵϵ
\alpha = \frac12ln\frac{1-\epsilon}\epsilon
α=21lnϵ1−ϵ
import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_gaussian_quantiles
from sklearn.metrics import classification_report
# 生成二维正太分布
x1,y1 = make_gaussian_quantiles(n_samples = 500,n_features = 2,n_classes = 2)
x2,y2 = make_gaussian_quantiles(mean = (3,3),n_samples = 500,n_features = 2,n_classes = 2)
xdata = np.concatenate((x1,x2))
ydata = np.concatenate((y1,1-y2))
plt.scatter(xdata[:,0],xdata[:,1],c=ydata)
plt.show()
# 画图函数
def plot(model):
xmin,xmax = xdata[:,0].min()-1,xdata[:,0].max()+1
ymin,ymax = xdata[:,1].min()-1,xdata[:,1].max()+1
xx,yy = np.meshgrid(np.arange(xmin,xmax,0.02),
np.arange(ymin,ymax,0.02))
z = model.predict(np.c_[xx.ravel(),yy.ravel()])
z = z.reshape(xx.shape)
cs = plt.contourf(xx,yy,z)
plt.scatter(xdata[:,0],xdata[:,1],c=ydata)
plt.show()
# 建立Adaboost模型
model = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3),n_estimators = 10)
model.fit(xdata,ydata)
plot(model)
生成的数据集如下:
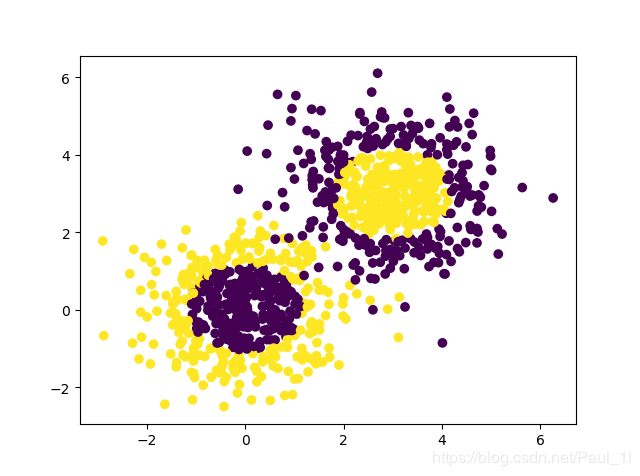
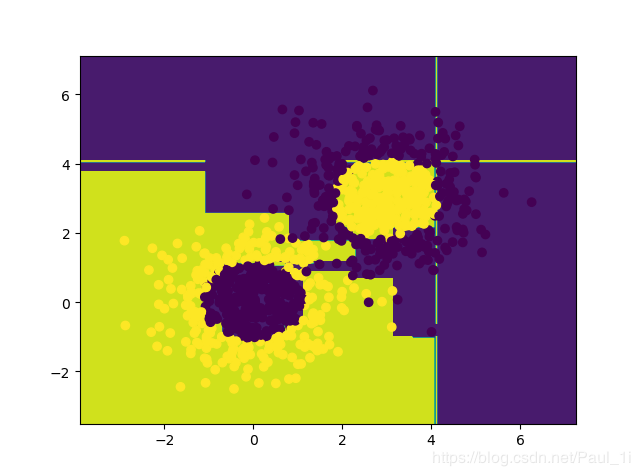
分类结果如下:
作者:木子六日