机器学习——基于Bagging的集成学习:随机森林(Random Forest)及python实现
“三个臭皮匠赛过诸葛亮”——弱分类器组合成强分类器。
Q1.什么是随机森林?
随机森林顾名思义就是一片森林,其中有各种各样的树,其实,随机森林是基于决策树构成的,一片森林中的每一颗树就是一个决策树。想了解决策树算法详情请戳☞决策树原理及其实现☜
Q2.为什么叫随机森林?
随机森林中“随机”一词主要在于两点:“随机”取样;“随机”抽取特征。
了解以上两点,我们先从集成学习入手:
集成学习的标准定义是:在原始数据上构建多个分类器,然后在分类未知样本时聚集它们的预测结果。简单理解就是:我们对多个训练数据集构建不同的分类器,再将这些分类器分别对测试集进行预测,将预测结果按照某种标准组合起来。其中不同的分类器称为基分类器,组合后的分类器称为组合分类器。
而这种组合方法最常见的有两种:Bagging,Boosting。前者对不同数据集构建的基分类器之间相互独立,也就是各自训练各自的,互不影响。而后者基分类器的构成总是依赖于上一个分类器的分类结果,常见的Adaboost方法就是典型的boosting方法,下一个的分类器的构建依赖于上一次分类器错分的样本,总是对错分的样本给予更大的权重,(也就是说,下一次抽到上次分错的样本的可能性更大,对其不断训练)。bagging和Boosting方法的流程图示如下:
bagging:
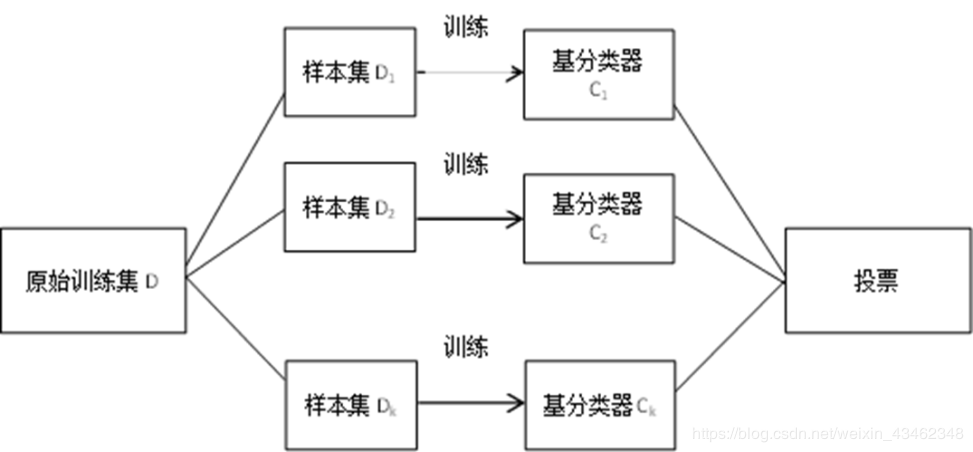
boosting:
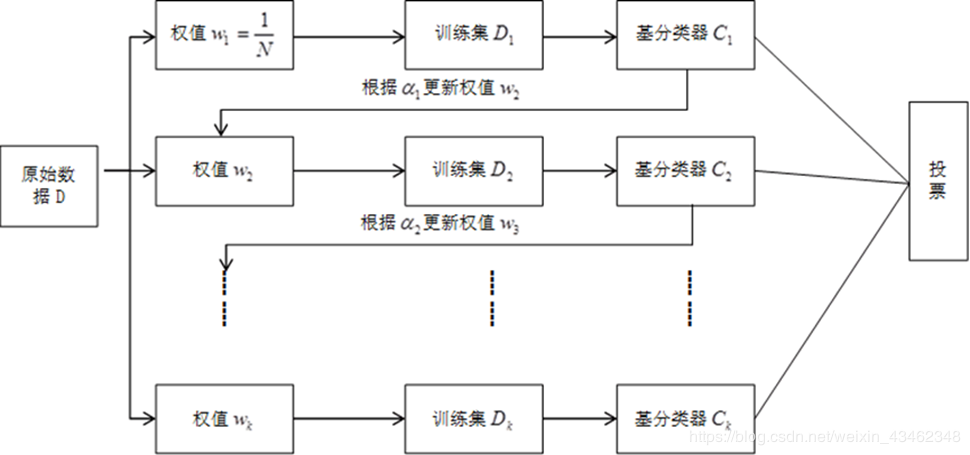
1、Bootstrap自助抽样——“随机”之一
Bagging为Bootstrap aggregating直译为自助聚集算法,其中Bootstrap是一种自助抽样方法,可以简单的理解为可重复抽样。把bootstrap理解成每次取原数据集的一部分装入一个袋中作为一个子样本,其特点特点特点是每次bootstrap结束后总会有一些样本始终没有被抽到,这些没有被抽到的样本称为OOB(Out Of Bag)。
可以看到几乎每一本机器学习教材都有涉及到“0.632采样”,其中0.632代表的是原数据中总有63.2%的数据参与模型训练,而剩余的26.8%的样本就是OOB样本。
PS.OOB误差:是指用全部数据进行训练,其中63.2%的样本训练,剩下26.8%的样本作为测试集预测。
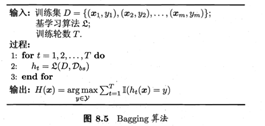
2、Bagging的优点
以单个决策树为基分类器,建立了25棵树(基分类器),对任何一个样本而言,平均或多数表决 原则下,当且仅当有13棵以上的树判断错误的时候,随机森林才会判断错误。假设单独一棵决策树的错误率在0.35(ε\varepsilonε)上下浮动,组合分类器误差率为:e=∑i=1325C25iεi(1−ε)25−i=0.06e=\sum_{i=13}^{25}C_{25}^i \varepsilon^i(1-\varepsilon)^{25-i}=0.06e=i=13∑25C25iεi(1−ε)25−i=0.06 可见,组合分类器的精度有着较大的提升。但是,是否每个分类器的组合都有此功效呢?不见得。在定义中,明确定义了“弱分类器”可组合成“强分类器”,那么,什么样的分类器才可成的上市“弱分类器”?一般,我们认为,分类的错误率小于0.5的分类器为弱分类器(可以思考,如果一个分类器错误率大于0.5,还不如随机猜测来的好些,哪里称得上“弱”,此时大可说成“差”)也可通过python做图如下:对于错误率小于0.5的分类器的组合效果远超想象,下面我们通过一个例子更好的了解一下bagging的运作方式。
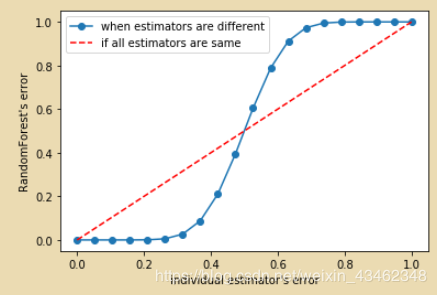
例:取《数据挖掘导论》5.4节的案例分别对比单个分类器和bagging组合分类器的效果:
| x | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 |
对决策树内容熟悉的小伙伴知道CART决策树具有对连续属性离散化的功能。主要方法步骤是:
1、对连续变量取值进行排序(本例已排序);
2、取每两个数的中点为阈值进行划分(首尾自动±间隔/2);
3、计算每种划分的gini系数,选取使gini值降低最多的阈值作为分割点。
本文取k=10即抽取10个自助样本,对每个样本建立一个cart树分类器,10个分类器的分类结果如下所示:
| k | x=0.1 | x=0.2 | x=0.3 | x=0.4 | x=0.5 | x=0.6 | x=0.7 | x=0.8 | x=0.9 | x=1.0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| … | … | … | … | … | … | … | … | … | … | … |
| 8 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 |
| 9 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 |
| 10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 和 | 2 | 2 | 2 | -6 | -6 | -6 | -6 | 2 | 2 | 2 |
| 组合分类器 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 |
| 实际类 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 |
以thres=0.35和thres=0.75为例:
y′={1,x≤0.35−1,x>0.35y'=\begin{cases} 1,x\leq 0.35\\ -1,x>0.35 \end{cases}y′={1,x≤0.35−1,x>0.35 y′={−1,x≤0.751,x>0.75y'=\begin{cases} -1,x\leq 0.75\\ 1,x>0.75 \end{cases}y′={−1,x≤0.751,x>0.75此时,准确率最高,达到70%
我们将10个分类器的分类结果进行组合:选择多数表决的方法,即少数服从多数。得到组合分类器的分类结果和实际类一致,集成模型准确率达到100%。
本文讨论的随机森林算法就是基于bagging的方法,即对每个数据集建立差异性的Cart决策树模型,将不同模型在测试集上的结果采取投票的方法进行整合。随机森林在分类问题中使用分类树,回归问题中使用回归树。
随机森林分类随机森林的步骤:
1、bootstrap抽取样本子集;
2、每个样本子集训练一棵CART分类树;
3、将每棵CART树的分类结果进行投票,得到结果即为随机森林的预测。
第二个“随机”——随机抽取样本子集
如果每个样本的特征维度为M,指定一个常数m<<M,随机地从M个特征中选取m个特征子集,每次树进行分裂时,从这M个特征中选择最优的;每个节点都将随机选择m(m<M)个特定的变量,然后运用这m个变量来确定最佳的分裂点。在决策树的生成过程中,m的值通常为:m=sqrt(p)m = sqrt(p)m=sqrt(p) or log(p)log(p)log(p)
注:每棵树都尽最大程度的生长,并且没有剪枝过程。
与分类不同在于:
1、目标变量是数值,模型评估指标为:“MSE/MAE/R2R^2R2”;分类为:“accuracy”
2、组合方法不同,回归为:将所有基分类器的预测结果求平均;分类为:投票
本例为简单实现,在真实数据集及完整调参参见:随机森林实现及调参
随机森林分类0需要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
1、 数据分割-红酒数据
wine = load_wine()
x = wine.data
y = wine.target
xtrain,xtest,ytrain,ytest = train_test_split(x,y,test_size=0.3)
2、 建模
clf = DecisionTreeClassifier(random_state=18)
clf = clf.fit(xtrain,ytrain)
rf = RandomForestClassifier(random_state=18)
rf = rf.fit(xtrain,ytrain)
accuracy1 = clf.score(xtest,ytest)
accuracy2 = rf.score(xtest,ytest)
print("单个树 :{}".format(accuracy1))
print("随机森林 :{}".format(accuracy2))
3、 交叉验证
rf_cv = cross_val_score(rf,x,y,cv=10)
clf_cv = cross_val_score(clf,x,y,cv=10)
plt.plot(range(1,11),rf_cv,label="RandomForest")
plt.plot(range(1,11),clf_cv,label="DecisionTree")
plt.legend()
plt.show()
4、 调参
(1) 确定最优树个数
best_ntree = []
for i in range(1,200):
rf = RandomForestClassifier(n_estimators=i+1,n_jobs=-1)
rf_cv = cross_val_score(rf,x,y,cv=10).mean()
best_ntree.append(rf_cv)
print(max(best_ntree),np.argmax(best_ntree)+1)
plt.figure(figsize=[20,5])
plt.plot(range(1,200),best_ntree)
plt.show()
(2) 袋外估计
rf = RandomForestClassifier(n_estimators=25)
rf = rf.fit(xtrain,ytrain)
score = rf.score(xtest,ytest)
score # 常规训练集测试集
5、预测
rf.predict_proba(xtest) # 预测概率
rf = RandomForestClassifier(n_estimators=20,random_state=18,oob_score=True)
rf = rf.fit(x, y)
rf.oob_score_
随机森林回归
0、 导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import load_boston
1、 数据分割
boston = load_boston()
x = boston.data
y = boston.targe
2、 建模
rfr = RandomForestRegressor(n_estimators=100,random_state=18)
3、 模型评估
score = cross_val_score(rfr,x,y,cv=10,scoring="neg_mean_squared_error")
作者:whether-or-not