python机器基础逻辑回归与非监督学习

一、逻辑回归

1.模型的保存与加载

2.逻辑回归原理

①逻辑回归的输入

②sigmoid函数

③逻辑回归的损失函数

④逻辑回归特点

3.逻辑回归API

4.逻辑回归案例

①案例概述

②具体流程

5.逻辑回归总结

二、非监督学习

1.k-means聚类算法原理

2.k-means API

3.聚类性能评估

①性能评估原理

②性能评估API

模型训练好之后，可以直接保存，需要用到joblib库。保存的时候是pkl格式，二进制，通过dump方法保存。加载的时候通过load方法即可。

安装joblib：conda install joblib

保存：joblib.dump(rf, 'test.pkl')

加载：estimator = joblib.load('模型路径')

加载后直接将测试集代入即可进行预测。

逻辑回归是一种分类算法，但该分类的标准，是通过h(x)输入后，使用sigmoid函数进行转换，同时根据阈值，就能够针对不同的h(x)值，输出0-1之间的数。我们将这个0-1之间的输出，认为是概率。假设阈值是0.5，那么，大于0.5的我们认为是1，否则认为是0。逻辑回归适用于二分类问题。

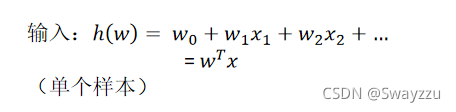
可以看出，输入还是线性回归的模型，里面还是有权重w，以及特征值x，我们的目标依旧是找出最合适的w。

该函数图像如下：

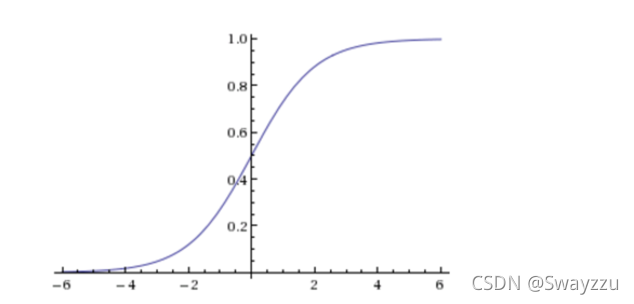
该函数公式如下：

z就是回归的结果h(x)，通过sigmoid函数的转化，无论z是什么值，输出都是在0-1之间。那么我们需要选择最合适的权重w，使得输出的概率及所得结果，能够尽可能地贴近训练集的目标值。因此，逻辑回归也有一个损失函数，称为对数似然损失函数。将其最小化，便可求得目标w。

损失函数在y=1和0的时候的函数图像如下：

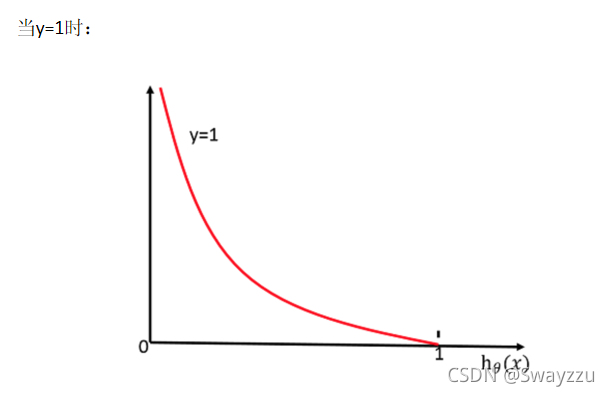
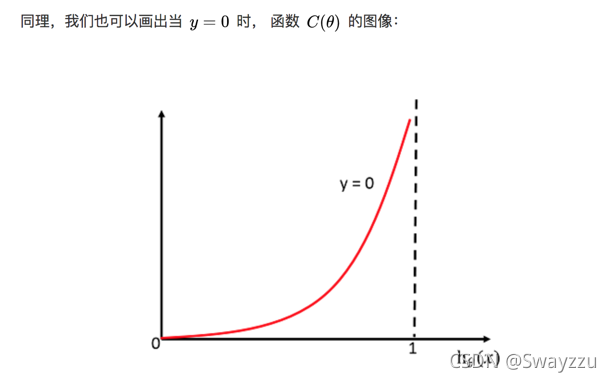
由上图可看出，若真实值类别是1，则h(x)给出的输出，越接近于1，损失函数越小，反之越大。当y=0时同理。所以可据此，当损失函数最小的时候，我们的目标就找到了。

逻辑回归也是通过梯度下降进行的求解。对于均方误差来说，只有一个最小值，不存在局部最低点；但对于对数似然损失，可能会出现多个局部最小值，目前没有一个能完全解决局部最小值问题的方法。因此，我们只能通过多次随机初始化，以及调整学习率的方法来尽量避免。不过，即使最后的结果是局部最优解，依旧是一个不错的模型。

sklearn.linear_model.LogisticRegression

其中penalty是正则化方式，C是惩罚力度。

给定的数据中，是通过多个特征，综合判断肿瘤是否为恶性。

由于算法的流程基本一致，重点都在于数据和特征的处理，因此本文中不再详细阐述，代码如下：

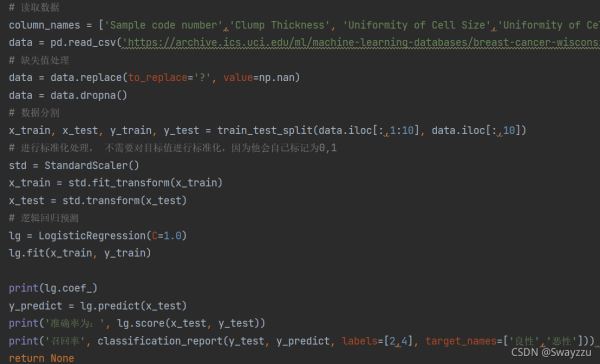
注意：

逻辑回归的目标值不是0和1，而是2和4，但不需要进行处理，算法中会自动标记为0和1

算法预测完毕后，如果想看召回率，需要注意对所分的类别给出名字，但给名字之前需要先贴标签。见上图。否则方法不知道哪个是良性，哪个是恶性。贴标签的时候顺序需对应好。

一般情况下，哪个类别的样本少，就按照哪个来去判定。比如恶性的少，就以“判断属于恶性的概率是多少”来去判断

应用：广告点击率预测、是否患病等二分类问题

优点：适合需要得到一个分类概率的场景

缺点：当特征空间很大时，逻辑回归的性能不是很好 （看硬件能力）

非监督学习就是，不给出正确答案。也就是说数据中没有目标值，只有特征值。

假设聚类的类别为3类，流程如下：

①随机在数据中抽取三个样本，作为类别的三个中心点

②计算剩余的点分别道三个中心点的距离，从中选出距离最近的点作为自己的标记。形成三个族群

③分别计算这三个族群的平均值，把三个平均值与之前的三个中心点进行比较。如果相同，结束聚类，如果不同，把三个平均值作为新的聚类中心，重复第二步。

sklearn.cluster.KMeans

通常情况下，聚类是做在分类之前。先把样本进行聚类，对其进行标记，接下来有新的样本的时候，就可以按照聚类所给的标准进行分类。

简单来说，就是类中的每一个点，与“类内的点”的距离，以及“类外的点”的距离。距离类内的点，越近越好。而距离类外的点，越远越好。

如果sc_i 小于0，说明a_i 的平均距离大于最近的其他簇。 聚类效果不好

如果sc_i 越大，说明a_i 的平均距离小于最近的其他簇。 聚类效果好

轮廓系数的值是介于 [-1,1] ，越趋近于1代表内聚度和分离度都相对较优

sklearn.metrics.silhouette_score

聚类算法容易收敛到局部最优，可通过多次聚类解决。

以上就是python机器基础逻辑回归与非监督学习的详细内容，更多关于python机器学习逻辑回归与非监督的资料请关注软件开发网其它相关文章！

逻辑回归 学习 回归 监督学习 Python