用Python做一张拥有渐变色的水平堆叠图
关键词:python、matplotlib、barh、堆叠
起源:做数据处理时候需要制造一张如下的图片:

示例图
恰逢最近在学Python,然后就想试一下用python去实现,因为稍微接触过matplotlib这个库,然后就想着用它去实现
首先通过查资料,才知道这种图的名字叫做“水平堆叠条状图”,然后使用Matplotlib.plot.barh()就可以实现水平堆叠的效果;水平或者垂直堆叠的效果,网上有挺多教程的了,这里就不再进行描述,主要是为了记录一下怎么去实现渐变色
一开始找资料,并没有找到这种堆叠图的渐变色怎么做出来
如果有大哥找到了简便方法,还请告知一下!然后就尝试着自己去写一些语句去实现;现在就将研究的流程做个记录
barh函数的参数很多,但是我们只关注几个参数:
X表示是上图中的 E1 E2 E3这样的坐标(可以理解为刻度值吧)
width表示的是当前堆叠部分的长度,这个值很关键!
left值是当前堆叠部分的起始点,这个值也很关键
color表示的是当前堆叠部分的颜色,遵循RGB顺序,但是它范围(0——0.1),即我们需将实际(R,G,B)值除以255再传入
alpha表示的是当前堆叠部分的颜色透明度,即和上面的color参数一起构成了(RGBA)
label表示的是当前堆叠部分的图形样例,即上图中的"label=二级指标1"那样的图例;该参数为空的时候不创建图例,如果不为空就会根据传入的字符串创建图例,默认是不支持中文的,如果要用中文,需要加以下这两句话在import matplotlib之后
#用来正常显示中文
plt.rcParams['font.sans-serif']=['SimHei','Times New Roman']
plt.rcParams['axes.unicode_minus']=False
`
然后讲讲怎么思考的
X的就是数轴上的显示的刻度值(你也可以给他重命名);
width表示的是堆叠(填充)长度,left是本次填充起始点,那么我们将这两个参数结合以下,就可以将本该一次填充完的长度,分成几次填充,再分别给这几次填充使用临近的RGB值,就会呈现一种渐变的效果
# 一次填充完成
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif']=['SimHei','Times New Roman'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False
# 网上找到的渐变色的RGB配色方案
Color1 = np.array([131, 175, 155])
Color2 = np.array([200, 200, 169])
Color3 = np.array([249, 205, 173])
x = ["E1"]
Y1 = np.array([0.1])
Y2 = np.array([0.3])
plt.barh(x, Y1, align="center", color=Color1 / 255, alpha=1, label="ONE1")
plt.barh(x, Y2, left=Y1, color=Color2 / 255, alpha=1, label="ONE2")
plt.legend()
plt.show()
上述代码运行以后的效果是这样的

然后基于我们上述的分析,我们将对“ONE2”色块运用参数:X,width,left,color进行分次填充实现渐变效果:
首先我们定义一个变量divid,这个变量将会决定了你分多少次填充
#填充次数,值越大渐变效果越好,但是计算量也会相应的增大
divid=20
其次我们将我们原来的填充量、颜色渐变差值分别分别除以divid
Y2_rate=Y2/divid
#用下一个颜色减去当前色快的颜色;这也将会解释了我后来的完整代码里,将会严格要求Color个数大于 Y 的个数
#实际上Color和Y大多数情况下是行向量,但仍然用“个数”来表述,为了更方便理解
Color_rate=(Color3-Color2)/divid
然后我们将会将这两个值在barh函数里进行使用
for i in range(divid):
if i==int( divid /2 ): #这里是去原先整个色块的中心RGB作为图例色
plt.barh(x,Y_rate,left=Y1+Y_rate*i,color=(Color1+i*Color_rate) / 255, alpha=1.0,label='ONE2')
else:
plt.barh(x,Y_rate,left=Y1+Y_rate*i,color=(Color1+i*Color_rate) / 255, alpha=1.0)
运行之后的效果为
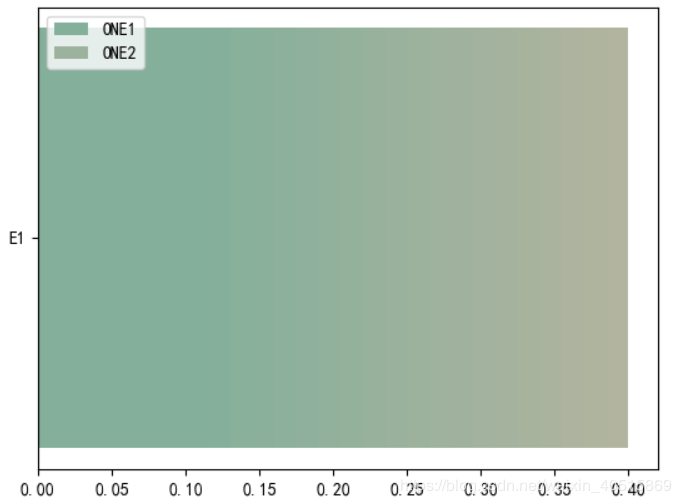
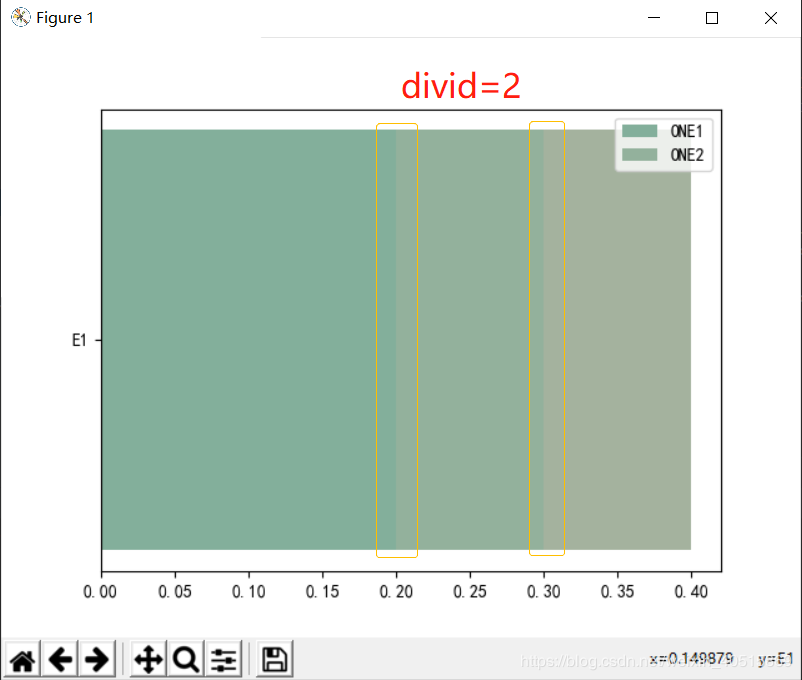
而为了说明divid在这里影响渐变效果我们将分辨用几个递增的divid值来进行演示
divid=2时候,出现了明显的分界线
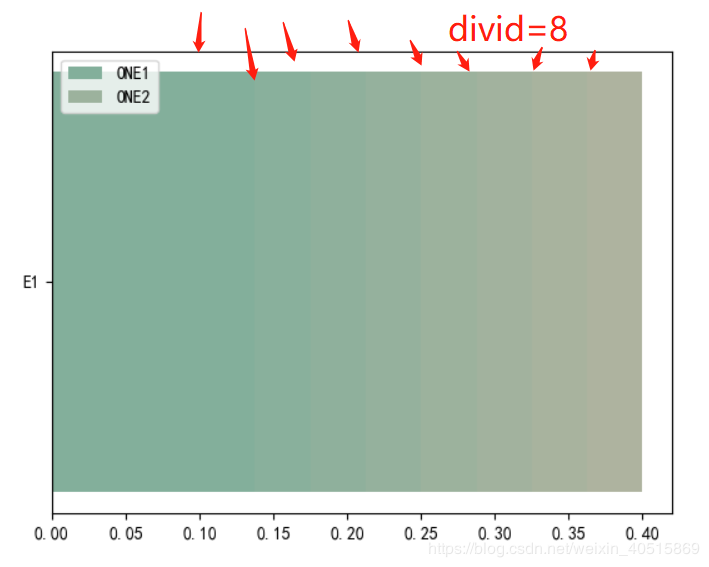
divid=8时候,分界线被淡化了,但还是隐约可见
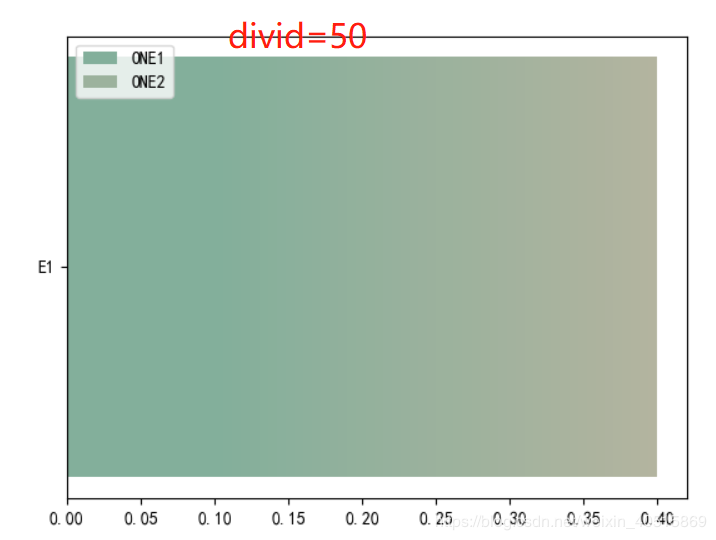
divid=50的时候,几乎看不到分界线了
以上效果仅仅是基于一个X 一个Y的色快渐变进行演示,是为了更好地演示方法和思路;但是实际应用中,X,Y都将会是较长的行向量,因此,需要斟酌一下divid的选择;
夜深了,还有些没阐述完的之后再补喽!
Em…我一定不会鸽的,gugugu~
作者:高攀中的稳健少年