CS231n assignment1 KNN部分用到的函数

Emma ·

更新时间:2024-11-13

· 945 次阅读

1. plt.rcParams

摘自：https://www.cnblogs.com/pacino12134/p/9776882.html

作用

设置matplotlib的配置参数，pylot使用rc配置文件来自定义图形的各种默认属性，称之为rc配置或rc参数。通过rc参数可以修改默认的属性，包括窗体大小、每英寸的点数、线条宽度、颜色、样式、坐标轴、坐标和网络属性、文本、字体等。

用法

rc参数存储在字典变量中，通过字典的方式进行访问。

例子

%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

摘自：https://www.cnblogs.com/psztswcbyy/p/11579055.html

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] # 用来显示中文标签
plt.rcParams['axes.unicode_minus']=False # 用来显示负号
plt.rcParams['figure.figsize'] = (16.0, 10.0) # 调整生成的图表最大尺寸
plt.rcParams['figure.dpi'] = 300 # 每英寸点数

常用参数

'figure.dpi': 100.0   每英寸点数
'figure.figsize': [6.0, 4.0]  生成的图表最大尺寸
'font.size': 10.0  字体大小
'hist.bins': 10  直方图分箱个数
'lines.linewidth': 1.5  线宽
'lines.marker': 'None'  标记样式
'savefig.format': 'png'  保存图片的格式
'savefig.jpeg_quality': 95  图片质量
'text.color': 'black'  文本颜色
'timezone': 'UTC'  时区格式

2. auto_reload

%load_ext autoreload
%autoreload 2

作用

摘自：https://segmentfault.com/a/1190000010758722?utm_source=tag-newest

自动重新加载更改的模块。在调试的过程中，如果代码发生更新，实现ipython中引用的模块也能自动更新。
是Jupyter的魔术命令（magic commands）之一。
详见：「官方」Built-in magic commands

3. np.shape()

numpy.array类型可使用 shape函数。list类型不能使用shape函数。

可以使用np.array(list A)进行转换即可使用。

PS：array转list：array BB.tolist()即可

4. enumerate()

摘自：https://www.runoob.com/python/python-func-enumerate.html

作用

将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，一般用在 for 循环当中。

语法

enumerate(sequence, [start=0])

参数

sequence --一个序列、迭代器或其他支持迭代对象。
start --下标起始位置

返回值

返回 enumerate(枚举) 对象。

例子

>>>seasons = ['Spring', 'Summer', 'Fall', 'Winter']
>>> list(enumerate(seasons))
[(0, 'Spring'), (1, 'Summer'), (2, 'Fall'), (3, 'Winter')]
>>> list(enumerate(seasons, start=1))       # 下标从 1 开始
[(1, 'Spring'), (2, 'Summer'), (3, 'Fall'), (4, 'Winter')]

普通for循环

>>>i = 0
>>> seq = ['one', 'two', 'three']
>>> for element in seq:
...     print i, seq[i]
...     i +=1
... 
0 one
1 two
2 three

for 循环使用 enumerate

>>>seq = ['one', 'two', 'three']
>>> for i, element in enumerate(seq):
...     print i, element
... 
0 one
1 two
2 three

# Visualize some examples from the dataset.
# We show a few examples of training images from each class.
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck'] #类别列表
num_classes = len(classes) #类别数目
samples_per_class = 7 #每个类别采样个数
for y, cls in enumerate(classes): #对列表的元素位置和元素进行循环，y表示元素位置（0,num_class），cls元素本身'plane'等
    idxs = np.flatnonzero(y_train == y) #找出标签中y类的位置
    idxs = np.random.choice(idxs, samples_per_class, replace=False) #从中选出我们所需的7个样本
    for i, idx in enumerate(idxs): #对所选的样本的位置和样本所对应的图片在训练集中的位置进行循环
        plt_idx = i * num_classes + y + 1 #在子图中所占位置的计算
        plt.subplot(samples_per_class, num_classes, plt_idx) #说明要画的子图的编号
        plt.imshow(X_train[idx].astype('uint8')) #画图
        plt.axis('off')
        if i == 0: 
            plt.title(cls) #写上标题，也就是类别名
plt.show() #显示

5. np.flatnonzero()

摘自：https://www.cnblogs.com/eilearn/p/9014864.html

作用

输入一个矩阵，扁平化后返回非零元素的位置（index）

例子


>>> import numpy as np
>>> x = np.arange(-2, 3)
>>> x
array([-2, -1,  0,  1,  2])
>>> np.flatnonzero(x)
array([0, 1, 3, 4])
>>> d = np.array([1,2,3,4,4,3,5,3,6])
>>> h = np.flatnonzero(d == 3)
>>> print (h)
[2 5 7]

6. np.random.choice()

摘自：https://blog.csdn.net/ImwaterP/article/details/96282230

numpy.random.choice(a, size=None, replace=True, p=None)

详见：官方解释

作用

Generates a random sample from a given 1-D array
从a(只要是ndarray都可以，但必须是一维的)中随机抽取数字，并组成指定大小(size)的数组。
除了numpy中的数组，python内建的list（列表）、tuple（元组）也可以使用。

参数

a : 1-D array-like or int
If an ndarray, a random sample is generated from its elements. If an int, the random sample is generated as if a were np.arange(a)

size : int or tuple of ints, optional
Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn. Default is None, in which case a single value is returned.

replace : boolean, optional
Whether the sample is with or without replacement
True表示可以取相同数字，False表示不可以取相同数字。默认可以选取相同数字。

p : 1-D array-like, optional
The probabilities associated with each entry in a. If not given the sample assumes a uniform distribution over all entries in a.
与数组a相对应，表示取数组a中每个元素的概率，默认为选取每个元素的概率相同。

例子用于生成随机数

>>> np.random.choice(5)#从[0, 5)中随机输出一个随机数
#相当于np.random.randint(0, 5)
2
>>> np.random.choice(5, 3)#在[0, 5)内输出五个数字并组成一维数组（ndarray）
#相当于np.random.randint(0, 5, 3)
array([1, 4, 1])

从数组、列表或元组中随机抽取
注意：不管是什么，它必须是一维的！

L = [1, 2, 3, 4, 5]#list列表
T = (2, 4, 6, 2)#tuple元组
A = np.array([4, 2, 1])#numpy,array数组,必须是一维的
A0 = np.arange(10).reshape(2, 5)#二维数组会报错
>>> np.random.choice(L, 5)
array([3, 5, 2, 1, 5])
>>> np.random.choice(T, 5)
array([2, 2, 2, 4, 2])
>>> np.random.choice(A, 5)
array([1, 4, 2, 2, 1])
>>> np.random.choice(A0, 5)#如果是二维数组，会报错
ValueError: 'a' must be 1-dimensional

参数replace

>>> np.random.choice(5, 6, replace=True)#可以看到有相同元素
array([3, 4, 1, 1, 0, 3])
>>> np.random.choice(5, 6, replace=False)#会报错，因为五个数字中取六个，不可能不取到重复的数字
ValueError: Cannot take a larger sample than population when 'replace=False'

参数p
p实际是个数组，大小（size）应该与指定的a相同，用来规定选取a中每个元素的概率，默认为概率相同

>>> aa_milne_arr = ['pooh', 'rabbit', 'piglet', 'Christopher']
>>> np.random.choice(aa_milne_arr, 5, p=[0.5, 0.1, 0.1, 0.3])
array(['pooh', 'pooh', 'pooh', 'Christopher', 'piglet'], dtype='|S11')
#可以看到，‘pooh’被选取的概率明显比其他几个高很多

————————————————
版权声明：本文为CSDN博主「ImwaterP」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/ImwaterP/article/details/96282230

7. np.reshape()

X.reshape(X.shape[0], -1).T

X.reshape(X.shape[0], -1).T可以将一个维度为(a,b,c,d)的矩阵转换为一个维度为(a, b∗c∗d)的矩阵。

例子

# Reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print(X_train.shape, X_test.shape,y_train.shape,y_test.shape)

8. np.linalg.norm()

摘自：https://blog.csdn.net/hqh131360239/article/details/79061535

x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)

linalg=linear（线性）+algebra（代数），norm则表示范数。

作用

求范数

参数

x: 表示矩阵（也可以是一维）

ord：范数类型

向量的范数：
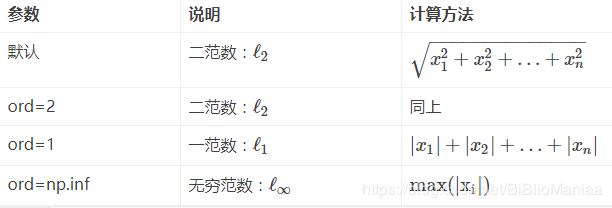
在这里插入图片描述
矩阵的范数：

ord=1：列和的最大值

ord=2：|λE-ATA|=0，求特征值，然后求最大特征值得算术平方根
(matlab在线版，计算ans=ATA，[x,y]=eig(ans)，sqrt(y)，x是特征向量，y是特征值)

ord=∞：行和的最大值

ord=None：默认情况下，是求整体的矩阵元素平方和，再开根号。（没仔细看，以为默认情况下就是矩阵的二范数，修正一下，默认情况下是求整个矩阵元素平方和再开根号）

axis：处理类型

axis=1表示按行向量处理，求多个行向量的范数

axis=0表示按列向量处理，求多个列向量的范数

axis=None表示矩阵范数。

keepdims：是否保持矩阵的二维特性

True表示保持矩阵的二维特性，False相反
————————————————
版权声明：本文为CSDN博主「IIYMGF」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/hqh131360239/article/details/79061535

例子

# Now implement the fully vectorized version inside compute_distances_no_loops
# and run the code
dists_two = classifier.compute_distances_no_loops(X_test)
# check that the distance matrix agrees with the one we computed before:
difference = np.linalg.norm(dists - dists_two, ord='fro')
print('No loop difference was: %f' % (difference, ))
if difference < 0.001:
    print('Good! The distance matrices are the same')
else:
    print('Uh-oh! The distance matrices are different')

输出：

Difference was: 0.000000
Good! The distance matrices are the same

9. *args, **kwargs

*args表示任何多个无名参数，它是一个tuple

**kwargs表示关键字参数，它是一个dict

例子


def foo(*args,**kwargs):
    print('args=',args)
    print('kwargs=',kwargs)
    print('************')
foo(1,2,3)
foo(a=1,b=2,c=3)
foo(1,2,a=3)

输出：

args= (1, 2, 3)
kwargs= {}
************
args= ()
kwargs= {'a': 1, 'c': 3, 'b': 2}
************
args= (1, 2)
kwargs= {'a': 3}

# Let's compare how fast the implementations are
def time_function(f, *args):
    """
    Call a function f with args and return the time (in seconds) that it took to execute.
    """
    import time
    tic = time.time()
    f(*args)
    toc = time.time()
    return toc - tic
two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
print('Two loop version took %f seconds' % two_loop_time)
one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
print('One loop version took %f seconds' % one_loop_time)
no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
print('No loop version took %f seconds' % no_loop_time)
# You should see significantly faster performance with the fully vectorized implementation!
# NOTE: depending on what machine you're using, 
# you might not see a speedup when you go from two loops to one loop, 
# and might even see a slow-down.

10. np.sum

摘自：https://blog.csdn.net/leekingsen/article/details/76242244

sum(a, axis=None, dtype=None, out=None, keepdims=np._NoValue)

a是要进行加法运算的向量/数组/矩阵

axis : None or int or tuple of ints, optional
Axis or axes along which a sum is performed.
The default, axis=None, will sum all of the elements of the input array.
If axis is negative it counts from the last to the first axis.
If axis is a tuple of ints, a sum is performed on all of the axes
specified in the tuple instead of a single axis or all the axes as before.

axis的取值有三种情况：1.None，2.整数， 3.整数元组。
（在默认/缺省的情况下，axis取None）

>>> np.sum([0.5, 1.5])
2.0
>>> np.sum([0.5, 0.7, 0.2, 1.5], dtype=np.int32)
1
>>> np.sum([[0, 1], [0, 5]])
6

如果axis取None，即将数组/矩阵中的元素全部加起来，得到一个和。
如果axis为整数，axis的取值不可大于数组/矩阵的维度，且axis的不同取值会产生不同的结果。

>>> np.sum([[0, 1], [0, 5]], axis=0)
array([0, 6])
>>> np.sum([[0, 1], [0, 5]], axis=1)
array([1, 5])

++当axis为0时,是压缩行,即将每一列的元素相加,将矩阵压缩为一行
++当axis为1时,是压缩列,即将每一行的元素相加,将矩阵压缩为一列(这里的一列是为了方便理解说的，实际上，在控制台的输出中，仍然是以一行的形式输出的)
++当axis取负数的时候，对于二维矩阵，只能取-1和-2（不可超过矩阵的维度）。
++++当axis=-1时，相当于axis=1的效果，当axis=-2时，相当于axis=0的效果。
如果axis为整数元组（x，y），则是求出axis=x和axis=y情况下得到的和。

>>> np.sum([[0,1],[0,5]],axis=(0,1))
6
>>> np.sum([[0,1],[0,5]],axis=(1,0))
6

另外，需要注意的是:如果要输入两个数组/矩阵/向量进行相加,那么就要先把两个数组/矩阵/向量用一个括号括起来,形成一个元组,这样才能够进行相加。因为numpy.sum的运算实现本质是通过矩阵内部的运算实现的。

当然,如果只是向量/数组之间做加法运算,可以直接让两个向量/数组相加,但前提是它们必须为numpy的array数组才可以,否则只是单纯的列表相加


>>>v1 = [1, 2]
>>>v2 = [3, 4]
>>>v1 + v2
[1, 2, 3, 4]
>>>v1 = numpy.array[1, 2]
>>>v2 = numpy.array[3, 4]
>>>v1 + v2
[4, 6]

keepdims主要用于保持矩阵的二维特性
————————————————
版权声明：本文为CSDN博主「Leekingsen」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/leekingsen/article/details/76242244

11. np.zeros()

np.zeros(shape, dtype=float, order='C')

返回来一个给定形状和类型的用0填充的数组；

12. np.dot()

官方文档

摘自https://www.cnblogs.com/luhuan/p/7925790.html

dot()函数可以通过numpy库调用，也可以由数组实例对象进行调用。a.dot(b) 与 np.dot(a,b)效果相同。

作用

求内积、矩阵积。

例子

1.如果处理的是一维数组，则得到的是两数组的內积

In : d = np.arange(0,9)
Out: array([0, 1, 2, 3, 4, 5, 6, 7, 8])
In : e = d[::-1]
Out: array([8, 7, 6, 5, 4, 3, 2, 1, 0])
In : np.dot(d,e) 
Out: 84

2.如果是二维数组（矩阵）之间的运算，则得到的是矩阵积（mastrix product）

In : a = np.arange(1,5).reshape(2,2)
Out:
array([[1, 2],
       [3, 4]])
In : b = np.arange(5,9).reshape(2,2)
Out:
array([[5, 6],
       [7, 8]])
In : np.dot(a,b)
Out:
array([[19, 22],
       [43, 50]])

13. np.argsort()

numpy.argsort(a, axis=-1, kind=’quicksort’, order=None)

摘自https://www.cnblogs.com/lucas-zhao/p/11697203.html

作用

将矩阵a按照axis从小到大排序，并返回排序后的下标

一维数组

>>> import numpy as np
>>> x = np.array([1,4,3,-1,6,9])
>>> x
array([ 1,  4,  3, -1,  6,  9])
>>> x.argsort()
array([3, 0, 2, 1, 4, 5])

二维数组

>>> x = np.array([[1,5,4],[-1,6,9]])
>>> x
array([[ 1,  5,  4],
       [-1,  6,  9]])

沿着行向下(每列)的元素进行排序

>>> np.argsort(x,axis=0)
array([[1, 0, 0],
       [0, 1, 1]])

沿着列向右(每行)的元素进行排序

>>> np.argsort(x,axis=1)
array([[0, 2, 1],
       [0, 1, 2]])

数组x的最小值

x[x.argsort()[0]]

或者用argmin()函数

x[x.argmin()]

数组x的最大值

x[x.argsort()[-1]]  # -1代表从后往前反向的索引

或者用argmax()函数,

x[x.argmax()]

输出排序后的数组

x[x.argsort()]
# 或
x[np.argsort(x)]

例子

closest_y = self.y_train[np.argsort(dists[i,:])[:k]]

argsort函数返回的是数组值从小到大的索引值

np.argsort()[num]

形式详见【numpy】np.argsort()函数

14. np.bincount()

摘自：https://blog.csdn.net/weixin_42280517/article/details/89788643

numpy.bincount(x, weights=None, minlength=None)

输入数组x需要是非负整数，且是一维数组。

作用

计算每个非负数出现的次数、

参数 weights 权重
若不指定权重，则默认x每个位置上的权重相等且为1。若给定不同位置的权重，则返回加权和。 minlength 最小长度
若不规定最小bin的个数，则默认的个数为（x的最大值+1）。比如最大值是2，则bin的个数为3，即[0 1 2]。
若规定bin的个数（需大于默认值否则无效），则bin的个数等于设定值。比如

>>> np.bincount(np.array([3,1,9]), minlength=8)
array([0, 1, 0, 1, 0, 0, 0, 0, 0, 1])

若不指定minlength，输出的个数应该为9+1=10个。但此时指定的minlength小于10，小于默认状态下的数量，参数不再作用。返回的长度仍为10。

>>> np.bincount(np.array([3,1,9]), minlength=20)
array([0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])

指定的minlength大于10，那么返回的长度就是20。

例子

y_pred[i] = np.argmax(np.bincount(closest_y))

统计closest_y中每一项标签出现的次数，再输出最大次数的closest_y标签。

>>> np.bincount(np.arange(5))
array([1, 1, 1, 1, 1])
>>> np.bincount(np.array([0, 1, 1, 3, 2, 1, 7]))
array([1, 3, 1, 1, 0, 0, 0, 1])
>>> x = np.array([0, 1, 1, 3, 2, 1, 7, 23])
>>> np.bincount(x).size == np.amax(x)+1
True

————————————————
版权声明：本文为CSDN博主「徐亦快」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_42280517/article/details/89788643

更多关于统计数组的值出现次数的方法详见：numpy 统计数组的值出现次数与np.bincount()详细解释

15. np.argmax()

argmax(a, axis=None, out=None)返回给定数组的最大索引

摘自：https://blog.csdn.net/weixin_38145317/article/details/79650188

参数

out

If provided, the result will be inserted into this array. It should be of the appropriate shape and dtype.

例子对一维向量

>>> import numpy as np
>>> a = np.array([3, 1, 2, 4, 6, 1])
>>> b=np.argmax(a)#取出a中元素最大值所对应的索引，此时最大值位6，其对应的位置索引值为4，（索引值默认从0开始）
>>> print(b)
4

对二维向量（通常意义下的矩阵）a[ ][ ]

>>> import numpy as np
>>> a = np.array([[1, 5, 5, 2],
...               [9, 6, 2, 8],
...               [3, 7, 9, 1]])
>>> b=np.argmax(a, axis=0)#对二维矩阵来讲a[0][1]会有两个索引方向，第一个方向为a[0]，默认按列方向搜索最大值
>>> #a的第一列为1，9，3,最大值为9，所在位置为1，
>>> #a的第一列为5，6，7,最大值为7，所在位置为2，
>>> #此此类推，因为a有4列，所以得到的b为1行4列，
>>> print(b)
[1 2 2 1]
>>> c=np.argmax(a, axis=1)#现在按照a[0][1]中的a[1]方向，即行方向搜索最大值，
>>> #a的第一行为1，5，5，2,最大值为5（虽然有2个5，但取第一个5所在的位置），索引值为1，
>>> #a的第2行为9，6，2，8,最大值为9，索引值为0，
>>> #因为a有3行，所以得到的c有3个值，即为1行3列
>>> print(c)
[1 0 2]

3.对于三维矩阵a[ ][ ][ ],情况最为复杂，但在lstm中应用最广

>>> import numpy as np
>>> a = np.array([
...               [
...                   [1, 5, 5, 2],
...                   [9, -6, 2, 8],
...                   [-3, 7, -9, 1]
...               ],
...  
...               [
...                   [-1, 7, -5, 2],
...                   [9, 6, 2, 8],
...                   [3, 7, 9, 1]
...               ],
...             [
...                   [21, 6, -5, 2],
...                   [9, 36, 2, 8],
...                   [3, 7, 79, 1]
...               ]
...             ])
>>> b=np.argmax(a, axis=0)#对于三维度矩阵，a有三个方向a[0][1][2]
>>> #当axis=0时，是在a[0]方向上找最大值，即两个矩阵做比较，具体
>>> #(1)比较3个矩阵的第一行，即拿[1, 5, 5, 2],
>>> #                         [-1, 7, -5, 2],
>>> #                         [21, 6, -5, 2],
>>> #再比较每一列的最大值在那个矩阵中，可以看出第一列1，-2，21最大值为21，在第 三个矩阵中，索引值为2
>>> #第2列5，7，6最大值为7，在第2个矩阵中，索引值为1.....，最终得出比较结果[2 1 0 0]
>>> #再拿出三个矩阵的第二行，按照上述方法，得出比较结果 [0 2 0 0]
>>> #一共有三个，所以最终得到的结果b就为3行4列矩阵
>>> print(b)
[[2 1 0 0]
 [0 2 0 0]
 [1 0 2 0]]
>>> c=np.argmax(a, axis=1)#对于三维度矩阵，a有三个方向a[0][1][2]
>>> #当axis=1时，是在a[1]方向上找最大值，即在列方向比较，此时就是指在每个矩阵内部的列方向上进行比较
>>> #(1)看第一个矩阵
>>>                   # [1, 5, 5, 2],
>>>                   # [9, -6, 2, 8],
>>>                   # [-3, 7, -9, 1]
>>> #比较每一列的最大值，可以看出第一列1，9，-3最大值为9，，索引值为1
>>> #第2列5，-6，7最大值为7，，索引值为2
>>> # 因此对第一个矩阵，找出索引结果为[1，2，0,1]
>>> #再拿出2个，按照上述方法，得出比较结果 [1 0 2 1]
>>> #一共有三个，所以最终得到的结果b就为3行4列矩阵
>>> print(c)
[[1 2 0 1]
 [1 0 2 1]
 [0 1 2 1]]
d=np.argmax(a, axis=2)#对于三维度矩阵，a有三个方向a[0][1][2]
>>> #当axis=2时，是在a[2]方向上找最大值，即在行方向比较，此时就是指在每个矩阵内部的行方向上进行比较
>>> #(1)看第一个矩阵
>>>                   # [1, 5, 5, 2],
>>>                   # [9, -6, 2, 8],
>>>                   # [-3, 7, -9, 1]
>>> #寻找第一行的最大值，可以看出第一行[1, 5, 5, 2]最大值为5，，索引值为1
>>> #第2行[9, -6, 2, 8],最大值为9，，索引值为0
>>> # 因此对第一个矩阵，找出行最大索引结果为[1，0，1]
>>> #再拿出2个矩阵，按照上述方法，得出比较结果 [1 0 2 1]
>>> #一共有三个，所以最终得到的结果d就为3行3列矩阵
>>> print(d)
[[1 0 1]
 [1 0 2]
 [0 1 2]]
>>> ###################################################################
>>> #最后一种情况，指定矩阵a[0, -1, :]，第一个数字0代表取出第一个矩阵（从前面可以看出a有3个矩阵）为
>>> # [1, 5, 5, 2],
>>> # [9, -6, 2, 8],
>>> # [-3, 7, -9, 1]
>>> #第二个数字“-1”代表拿出倒数第一行，为
>>> # [-3, 7, -9, 1]
>>> #这一行的最大索引值为1
>>>  
>>> # ，-1，代表最后一行
>>> m=np.argmax(a[0, -1, :])
>>> print(m)
1
>>>  
>>> #h,取a的第2个矩阵
>>> # [-1, 7, -5, 2],
>>> # [9, 6, 2, 8],
>>> # [3, 7, 9, 1]
>>> #的第3行
>>> # [3, 7, 9, 1]
>>> #的最大值为9，索引为2
>>> h=np.argmax(a[1, 2, :])
>>> print(h)
2
>>>  
>>> g=np.argmax(a[1,:, 2])#g,取出矩阵a，第2个矩阵的第3列为-5，2，9,最大值为9， 索引为2
>>> print(g)
2

————————————————
版权声明：本文为CSDN博主「wanghua609」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_38145317/article/details/79650188

16. np.array_split()/np.split()

split(ary, indices_or_sections, axis=0)np.split() 均等分割，不均等会报错
numpy.array_split(ary, indices_or_sections, axis=0)np.array_split() 不均等分割，不会报错

参数 ary
要切分的数组 indices_or_sections
如果是一个整数，就用该数平均切分，如果是一个数组，为沿轴切分的位置（左开右闭） axis
沿着哪个维度进行切向，默认为0，横向切分。为1时，纵向切分例子

>>> x = np.arange(8.0)
>>> np.array_split(x, 3)
[array([0., 1., 2.]), array([3., 4., 5.]), array([6., 7.])]

17. np.vstack()/np.hstack() 作用

np.vstack(): 沿着竖直方向将矩阵堆叠起来

np.hstack(): 沿着水平方向将数组堆叠起来

例子

import numpy as np
a=np.array([[ 8., 8.],[ 0., 0.]])
b=np.array([[ 1., 3.], [ 6., 4.]])
print np.vstack((a,b))  #将两个数组按行堆放在一起
[[8. 8.]
 [0. 0.]
 [1. 3.]
 [6. 4.]]
print np.hstack((a,b)# 将两个数组按列堆放在一起
[[8. 8. 1. 3.]
 [0. 0. 6. 4.]]

19. plt.scatter([k] * len(accuracies), accuracies)

摘自：https://blog.csdn.net/zzc15806/article/details/82629406

当我们使用arr = [[0]*5]5 初始化一个二维数组时，会得到一个55的数组，

In [1]: arr = [[0]*5]*5
In [2]: arr
Out[2]: 
[[0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0]]

然后对这个二维数组某个元素进行赋值，会发现整列都会被赋值，

In [3]: arr[0][0] = 1
In [4]: arr
Out[4]: 
[[1, 0, 0, 0, 0],
 [1, 0, 0, 0, 0],
 [1, 0, 0, 0, 0],
 [1, 0, 0, 0, 0],
 [1, 0, 0, 0, 0]]

这是因为 [[0]*5]*5 表示的是指向 [0]*5 这个列表的引用，所以当你修改某一个值时，整个列表都会被改变。

换一种初始化方式可以解决这个问题，

In [1]: arr = [[0]*5 for _ in range(5)]
In [2]: arr
Out[2]: 
[[0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0]]
In [3]: arr[0][0] = 1
In [4]: arr
Out[4]: 
[[1, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0]]

————————————————
版权声明：本文为CSDN博主「z小白」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/zzc15806/article/details/82629406

20. plt.errorbar() 作用

用于表现有一定置信区间的带误差数据
详见：plt.errorbar()函数解析（最清晰的解释）

21. list(seq)

将元组转换为列表

mask = list(range(num_training))
X_train = X_train[mask]
y_train = y_train[mask]
num_test = 500
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]

22. sorted()

sorted(iterable, key=None, reverse=False)sorted() 函数对所有可迭代的对象进行排序操作。

sort 与 sorted 区别

sort 是应用在 list 上的方法，sorted 可以对所有可迭代的对象进行排序操作。

list 的 sort 方法返回的是对已经存在的列表进行操作，而内建函数 sorted 方法返回的是一个新的 list，而不是在原来的基础上进行的操作。

参数

iterable – 可迭代对象。
key – 主要是用来进行比较的元素，只有一个参数，具体的函数的参数就是取自于可迭代对象中，指定可迭代对象中的一个元素来进行排序。
reverse – 排序规则，reverse = True 降序， reverse = False 升序（默认）。
详见：Python3 sorted() 函数

23. 给函数计时

  def time_function(f, *args):
    """
    Call a function f with args and return the time (in seconds) that it took to execute.
    """
    import time
    tic = time.time()
    f(*args)
    toc = time.time()
    return toc - tic

代码如上，只有几行，当实现了很好的封装和可用性。这里主要是用了Python中的可变参数和函数特性（函数名其实就是指向一个函数对象的引用，完全可以把函数名赋给一个变量，相当于给这个函数起了一个“别名”：）。
f是一个指向函数对象的引用别名；*args表示任何多个无名参数，它是一个tuple。
应用如下：

def time_function(f, *args):
    """
    Call a function f with args and return the time (in seconds) that 
    it took to execute.
    """
    import time
    tic = time.time()
    f(*args)
    toc = time.time()
    return toc - tic
def addition(a, b, c):
    return a + b + c
def subtract(a, b):
    return a - b
add_time_cost = time_function(addition, 3, 4, 5)
sub_time_cost = time_function(subtract, 3, 4)
print('add_time_cost:', add_time_cost)
print('sub_time_cost:', sub_time_cost)

————————————————
版权声明：本文为CSDN博主「许孝发」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/newmemory/article/details/80760561

参考：
Setup Instructions
作业链接
斯坦福cs231n课程记录——assignment1 KNN
斯坦福cs231n课程记录——assignment1 KNN
cs231n：python3.6.4对实验数据图像的读取，课后作业代码解释
k-Nearest Neighbor (kNN) exercise
欢迎来到实力至上主义的CS231n教室（一）机器学习基础
统计学习方法（k近邻）
cs231n作业：assignment1 - knn

作者：BiBlioManiaa

cs231n cs2 函数 knn

1024 个赞