哈夫曼编码的c实现
目录
设计思想
设计流程
实现代码
实验结果
实验结果与理论结果验证
参考文献
设计思想由数据结构学习的哈夫曼树的编程思想,可以先构造哈夫曼树,在构造哈夫曼编码。
哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式,可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。哈夫曼编码,主要目的是根据使用频率来最大化节省字符(编码)的存储空间。
设计流程 简易的理解就是,假如我有A,B,C,D,E五个字符,出现的频率(即权值)分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树,即取1,2构成新树,其结点为1+2=3,如图:



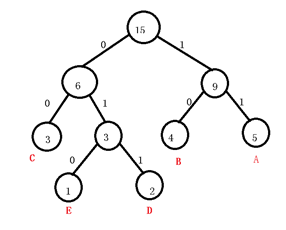
所以各字符对应的编码为:A->11,B->10,C->00,D->011,E->010 实现代码
/*********************************************************************************
* Copyright: (C) 2020 shx
* All rights reserved.
*
* Filename: tmp.c
* Description: This file
*
* Version: 1.0.0(04/20/2020)
* Author: tianjincheng
* ChangeLog: 1, Release initial version on "04/20/2020 10:08:09 AM"
*
********************************************************************************/
#define _CRT_SECURE_NO_WARNINGS
#include
#define H_MAXBIT 100
#define H_MAXVALUE 1000
#define H_MAXLEAF 30 //叶子节点数目
#define H_MAXNODE (((H_MAXLEAF)*2)-1) //节点数目
typedef struct //定义编码结构体
{
int bit[H_MAXBIT];
int start;
}HCodeType;
typedef struct //定义节点结构体
{
int weight;
int parent;
int lchild;
int rchild;
}HNodeType;
//构造哈夫曼树
void HuffmanTree(HNodeType HuffNode[H_MAXNODE], int n)
{
int i, j, m1, m2, x1, x2;
for (i = 0; i < 2*n-1; ++i)
{
HuffNode[i].weight = 0;
HuffNode[i].parent = -1;
HuffNode[i].lchild = -1;
HuffNode[i].rchild = -1;
}
for (i = 0; i < n; i++)
{
char *buf[5] = {"A","B","C","D","E"};
/*输入每个节点的权值*/
printf("输入[%s]节点的权值: \n", buf[i]);
scanf("%d", &HuffNode[i].weight);
}
/*构造哈夫曼树*/
for (i = 0; i < n - 1; i++)
{
m1 = m2 = H_MAXVALUE;
x1 = x2 = 0;
/*找出权值最小的节点,并合并为一个二叉树*/
for (j = 0; j < n + i; j++)
{
if (HuffNode[j].weight < m1&&HuffNode[j].parent == -1)
{
m2 = m1;
x2 = x1;
m1 = HuffNode[j].weight;
x1 = j;
}
else if (HuffNode[j].weight < m2 && HuffNode[j].parent == -1)
{
m2 = HuffNode[j].weight;
x2 = j;
}
}
HuffNode[x1].parent = n + i;
HuffNode[x2].parent = n + i;
HuffNode[n + i].weight = HuffNode[x1].weight + HuffNode[x2].weight;
HuffNode[n + i].lchild = x1;
HuffNode[n + i].rchild = x2;
}
}
int main()
{
char* buf[5] = { "A","B","C","D","E" };
HNodeType HufNode[H_MAXNODE];
HCodeType HufCode[H_MAXLEAF], cd;
int i, j, c, p, n;
printf("输入需要编码的节点数目:\n");
scanf("%d", &n);
if (n 6)
{
printf("输入参数不合法,请输入0<x<6\n");
return 0;
}
HuffmanTree(HufNode, n);
for (i = 0; i < n; i++)
{
cd.start = n - 1;
c = i;
p = HufNode[c].parent;
while (p != -1)
{
if (HufNode[p].lchild == c)
{
cd.bit[cd.start] = 0;
}
else
{
cd.bit[cd.start] = 1;
}
cd.start--;
c = p;
p = HufNode[c].parent;
}
for (j = cd.start + 1; j < n; j++)
{
HufCode[i].bit[j] = cd.bit[j];
HufCode[i].start = cd.start;
}
}
for (i = 0; i < n; i++)
{
printf("[%s]节点的哈夫曼编码为: ", buf[i]);
for (j = HufCode[i].start + 1; j < n; j++)
{
printf("%2d", HufCode[i].bit[j]);
}
printf("\n");
}
getchar();
system("pause");
return 0;
}
实验结果

实验结果与理论结果验证
实验结果:A(0): 1 1 , B(2): 1 0 C(2): 0 0 D(3):0 1 1 E(5): 0 1 0
理论结果:A(0): 1 1 , B(2): 1 0 C(2): 0 0 D(3):0 1 1 E(5): 0 1 0
参考文献
百度:《哈夫曼编码测的基本实现》
陈运《信息论与编码》第三版
作者:TianJCheng'Blog