C语言实现BMP图像处理(哈夫曼编码)

Elana ·

更新时间:2024-11-13

· 554 次阅读

哈夫曼(Huffman)编码是一种常用的压缩编码方法，是 Huffman 于 1952 年为压缩文本文件建立的。它的基本原理是频繁使用的数据用较短的代码代替，较少使用的数据用较长的代码代替，每个数据的代码各不相同。这些代码都是二进制码，且码的长度是可变的。

下面给出具体的 Huffman 编码算法：

(1) 首先统计出每个符号出现的频率，上例 S0 到 S7 的出现频率分别为 4/14，3/14，2/14，1/14，1/14，1/14，1/14，1/14。
(2) 从左到右把上述频率按从小到大的顺序排列。
(3) 每一次选出最小的两个值，作为二叉树的两个叶子节点，将和作为它们的根节点，这两个叶子节点不再参与比较，新的根节点参与比较。
(4) 重复(3)，直到最后得到和为 1 的根节点。
(5) 将形成的二叉树的左节点标 0，右节点标 1。把从最上面的根节点到最下面的叶子节点途中遇到的 0,1 序列串起来，就得到了各个符号的编码。

产生 Huffman 编码需要对原始数据扫描两遍。第一遍扫描要精确地统计出原始数据中，每个值出现的频率，第二遍是建立 Huffman 树并进行编码。由于需要建立二叉树并遍历二叉树生成编码，因此数据压缩和还原速度都较慢，但简单有效，因而得到广泛的应用。

第一步：实现哈夫曼编码与解码


#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>
#include <string.h>
// 结构体
typedef struct Tree
{
 int weight; // 权值
 int id;     // 后面解码用到
 struct Tree * lchild; // 左孩子
 struct Tree * rchild; // 右孩子
}TreeNode;
// 创建哈夫曼树
TreeNode* createTree(int *arr, int n)
{
 int i, j;
 TreeNode **temp, *hufmTree;
 temp = (TreeNode**)malloc(sizeof(TreeNode*)*n); // 创建结构体指针数组
 for (i = 0; i < n; ++i)
 {
  temp[i] = (TreeNode*)malloc(sizeof(TreeNode));
  temp[i]->weight = arr[i];
  temp[i]->lchild = temp[i]->rchild = NULL;
  temp[i]->id = i;
 }
 for (i = 0; i < n - 1; ++i)
 {
  int small1 = -1, small2; // 存储最小权值的两个节点
  for (j = 0; j < n; ++j)  // 第一步：找到最开始两个非空节点
  {
   if (temp[j] != NULL && small1 == -1)
   {
    small1 = j;
    continue;
   }
   if (temp[j] != NULL)
   {
    small2 = j;
    break;
   }
  }
  for (j = small2; j < n; ++j) // 找到权值最小的两个节点，并将最小的序号赋给small1，次小的赋给small2
  {
   if (temp[j] != NULL)
   {
    if (temp[j]->weight < temp[small1]->weight)
    {
     small2 = small1;
     small1 = j;
    }
    else if (temp[j]->weight < temp[small2]->weight)
    {
     small2 = j;
    }
   }
  }
  hufmTree = (TreeNode*)malloc(sizeof(TreeNode));
  hufmTree->lchild = temp[small1];
  hufmTree->rchild = temp[small2];
  hufmTree->weight = temp[small1]->weight + temp[small2]->weight;
  temp[small1] = hufmTree;
  temp[small2] = NULL;
 }
 free(temp);
 return hufmTree;
}
// 前序遍历
void PreOrderTraversal(TreeNode* hufmTree)
{
 if (hufmTree)
 {
  printf("%d", hufmTree->weight);
  PreOrderTraversal(hufmTree->lchild);
  PreOrderTraversal(hufmTree->rchild);
 }
}
// 哈夫曼编码
void hufmTreeCode(TreeNode* hufmTree,int depth)
{
 static int code[10],i;
 if (hufmTree)
 {
  if (hufmTree->lchild == NULL && hufmTree->rchild == NULL)
  {
   int i=0;
   printf("权值为%d的节点，哈夫曼编码为：", hufmTree->weight);
   for (i = 0; i < depth; ++i)
   {
    printf("%d", code[i]);
   }
   printf("\n");
  }
  else
  {
   code[depth] = 0;
   hufmTreeCode(hufmTree->lchild, depth + 1);
   code[depth] = 1;
   hufmTreeCode(hufmTree->rchild, depth + 1);
  }
 }
}
// 哈夫曼解码
// 思想：通过定位ID，找到源码中的位置
void hufmTreeDecode(TreeNode* hufmTree, char a[],char st[])
{
 int i,arr[100];
 TreeNode* temp;
 for (i = 0; i < strlen(a); ++i) // 转化字符串编码为数组编码
 {
  if (a[i] == '0')
   arr[i] = 0;
  else
   arr[i] = 1;
 }
 i = 0;
 while (i < strlen(a))
 {
  temp = hufmTree;
  while (temp->lchild != NULL && temp->rchild != NULL)
  {
   if (arr[i] == 0)
    temp = temp->lchild;
   else
    temp = temp->rchild;
   i++;
  }
  printf("%c", st[temp->id]);
 }
 printf("\n");
 free(temp);
}
int main()
{
 int i, n, arr[100];
 printf("输入需要创建的节点个数：\n");
 scanf("%d", &n);
 printf("输入权值：\n");
 for (i = 0; i < n; ++i)
  scanf("%d", &arr[i]);
 printf("\n请输入每个权值对应的字符:\n");
 char st[100];
 scanf("%s",st);
 // 创建哈夫曼树
 TreeNode* hufmTree;
 hufmTree = createTree(arr, n);
 // 哈夫曼编码
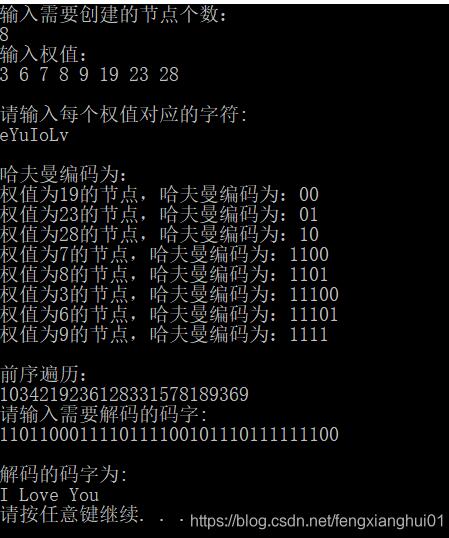
 printf("\n哈夫曼编码为：\n");
 hufmTreeCode(hufmTree, 0);
 // 遍历
 printf("\n前序遍历：\n");
 PreOrderTraversal(hufmTree);
 // 解码
 printf("\n请输入需要解码的码字:\n");
 char codeSt[100]; 
 scanf("%s",codeSt);
 printf("\n解码的码字为:\n");
 hufmTreeDecode(hufmTree, codeSt, st);
 free(hufmTree);
 system("pause");
 return 0;
}