JAVA十大排序中的-(归并排序)

Izellah ·

更新时间:2024-11-10

· 694 次阅读

前奏

该算法是采用分治法的典型应用,将一个无序序列分组诺干个，然后对该小组进行排序,排序完以后,将各个小组合并排序比较,直到将诺干个小组组合成一组就是一个有序列表了

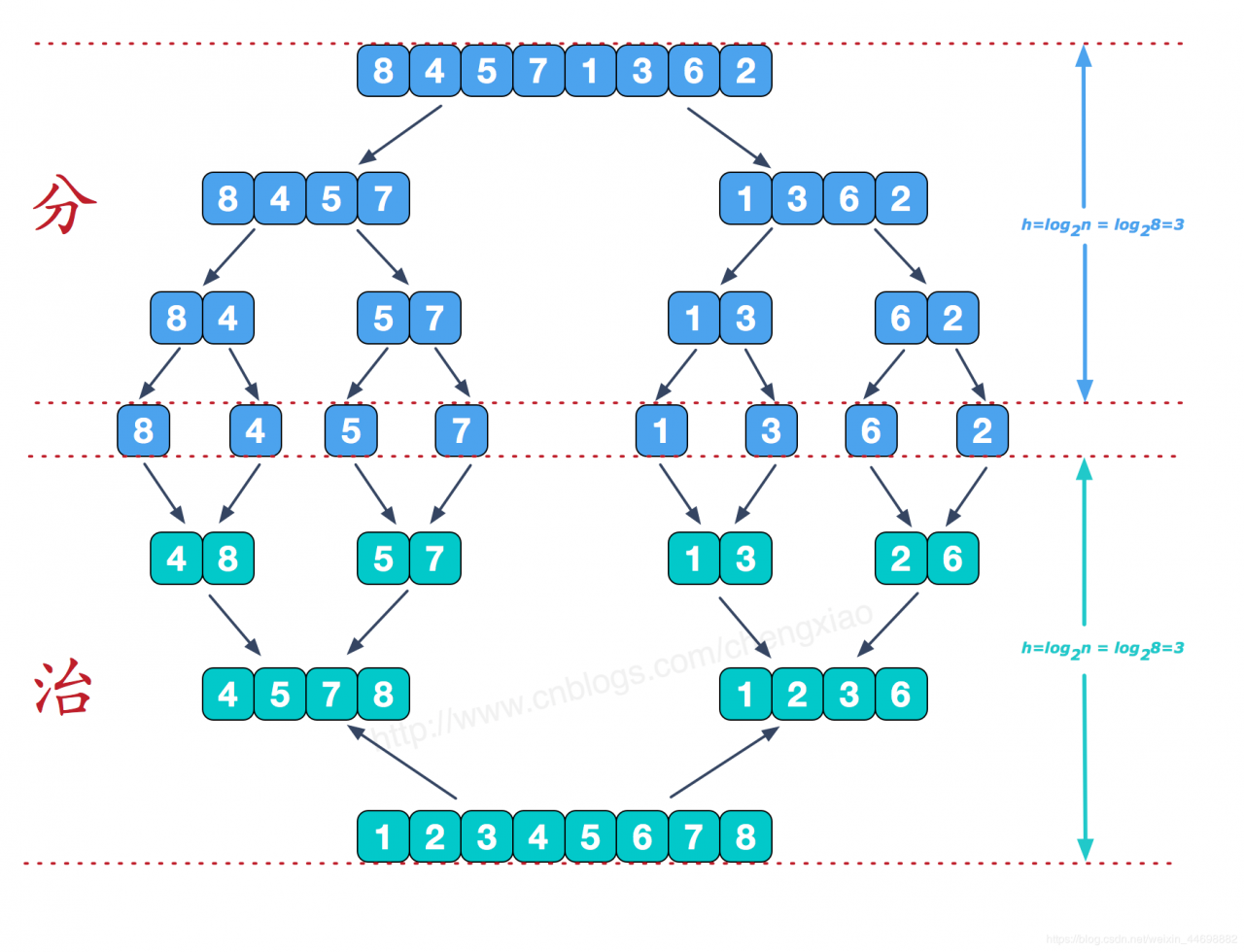
思路提示:使用了回溯思想、拆到不能再拆的时候才进行排序比较

1：将一个无序列表依次的回调拆分成诺干个小组(提示：小组里面的元素可以是一个最多是2个)先将左边的进行拆分合并排序,在执行右边的拆分排序
2：然后无法回调的时候就将当前小组内容进行合并排序,然后返回到拆分为当前层的层栈上进行合并排序,依次类推
提示：需要在创建一个同大小的数组 该数组是用来进行临时排序存储合并用的  所谓的空间换时间

课外仅供参考

如果与一组8000个数据的数组排序的情况下             时间差不多3毫秒不到 
如果与一组80000个数据的数组排序的情况下            时间差不多30毫秒不到
如果与一组800000个数据的数组排序的情况下           时间差不多150毫秒不到
如果与一组8000000个数据的数组排序的情况下          时间差不多1.3秒不到
如果与一组80000000个数据的数组排序的情况下         时间差不多15秒不到
归并是先使劲的递归递归到不能在递归才进行排序合并、而且快速排序排序一次在进行递归

图解 1

在这里插入图片描述

图解2 代码

注意：这里的count对应的索引值是当前区域的left ,然后将当前内容赋值给temp也是对应当前count索引
提示：如果将从小到大顺序变成从大到小顺序，改对应的将> 改成<

//归并排序方法
    public static void mergeSort(int [] array,int left ,int right,int [] tempArr){
        //左指针小于右指针代表还可以进行拆分分治
        if(left<right){
            //大致获取当前索引范围的中间值元素索引
            int middleIndex=(left+right)/2;
            //获取当前移动左指针
            int moveLeftPoint=left;
            int moveRightPoint=middleIndex+1;
            //创建一个用于当前范围的索引操作遍历
            int count=left;
            //由于还是可以拆分所以进行回溯数组拆分
            mergeSort(array,left,middleIndex,tempArr); //向左拆分直拆到拆成到范围只有一个元素无需拆分
            mergeSort(array,moveRightPoint,right,tempArr); //向右拆分
            //计算排序当前索引范围的元素
            while(moveLeftPoint<=middleIndex&&moveRightPointarray[moveRightPoint]){
                    //就将右指针对应的元素添加到count对应的索引位置种
                    tempArr[count++]=array[moveRightPoint];
                    moveRightPoint++;
                }else{
                    tempArr[count++]=array[moveLeftPoint];
                    moveLeftPoint++;
                }
            }
            //将其余的指针依次添加到tempArr
            while(moveLeftPoint<=middleIndex){
                tempArr[count++]=array[moveLeftPoint];
                moveLeftPoint++;
            }
            while(moveRightPoint<=right){
                tempArr[count++]=array[moveRightPoint];
                moveRightPoint++;
            }
            count=left;
            //将tempArr排好序的索引元素一次性赋值给array
            while(count<=right){
                array[count]=tempArr[count];
                count++;
            }
        }
    }

作者：丿旧城以西

归并排序排序 JAVA

1024 个赞