叶天帝对战黑暗至尊，多次濒临死境，却创出 分治算法（分治算法解决归并排序），小白也能看懂的归并
问题引入:
前文说到，叶天帝集结天庭众人攻打生命禁区，在此之前发生了一个小插曲，大黑狗偷了叶天帝的空间戒指，使得叶天帝无法携带大量的资源。为此，叶天帝闭关九九八十一天，创出了 0-1背包大法 ，这才顺利启程，一场大战缓缓拉开帷幕。
这一日，叶天帝与众位黑暗至尊展开了白热化的战斗，叶天帝虽强，但终归是双拳难敌四手，战况岌岌可危，叶天帝险象环生。在这千钧一发之际，只见大黑狗施展“行”字秘术，来到高空，一声大喝“叶小子，分治啊，逐个击破”，叶天帝突然顿悟，施展法门，将空间划分为若干个部分，后施展一气化三清秘术，化出分身去各个空间逐个击破。
此一战，叶天帝在战斗中濒临死境，却也创出了旷古奇法 分治。
分治的基本概念：
把一个任务分成形式和原任务相同，但规模更小的几个部分，然后逐个击破，分别完成，然后再处理完成后的完成后的子任务，将子任务的解进行合并，得到原任务的解。
此算法是许多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)等
分治法所能解决的问题一般具有以下几个特征：
（1）当问题的规模缩小到一定的程度时，就可以使用很简单的方法解决；
（2）该问题可以分解为若干个规模较小的、相同形式的子问题问题；
（3）通过子问题的解可以合并得出为该问题的解；
（4）该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。
如：斐波那契数列的求解过程，它虽然也可以采用类似“分而治之”的思路，但是它的多个子问题之间都会有交集，所以就不能采用普通的分治算法解决。
分治法解决问题的一般思路：
（1）分解。
（2）解决子问题，若不能解决，则再分解。
（3）合并，由子问题的解推出原问题的解。
几个典型分治算法的应用：
（1）排序（快排，归并）
（2）二分查找
（3）二叉树遍历(前序，中序，后序)
（4）大整数乘法
（5）几何问题(最近点对，凸包)
……
归并排序的思想：
（１）把前一半数组进行排序
（２）把后一半数组进行排序
（３）将前后两部分归并到一个新的有序数组，然后将这个有序数组再“赋值”给原来的数组，归并排序完成。
设计算法：
需要一个辅助数组T，用来存放排序的中间结果。 设定三个指针，po指向辅助数组首元素的位置，p1指向前半个数组的首元素的位置，p2指向后半个数组的首元素的位置。 扫描前后两个已经排好序的半数组，每次将较小的元素放在辅助数组的前面。 经过步骤 3 ，必将会有一个数组先放完，而另外一个数组中还有元素没有放进辅助数组。这时，只需将那个半数组没有放完的元素直接放进辅助数组即可。 将辅助数组拷贝给原数组。归并排序完成。 为什么不直接就输出辅助数组的元素，还费时间将它再拷贝给原数组？因为采用的是递归算法，每次的辅助数组只用到一部分，每次用完之后都会进行更新，它存放的只是排序的中间结果，并不是全部排好序的数组。所以，不能直接使用辅助数组。
图解核心算法：
第一步：p1，p2，po都指向各自数组的首部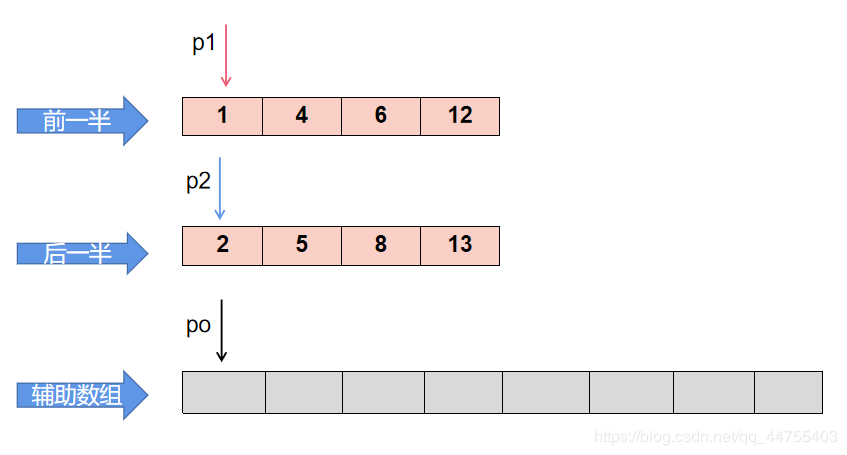
第二步：比较 p1 指向的值和 p2 的大小，将较小者放在 po 位置，然后指针后移。
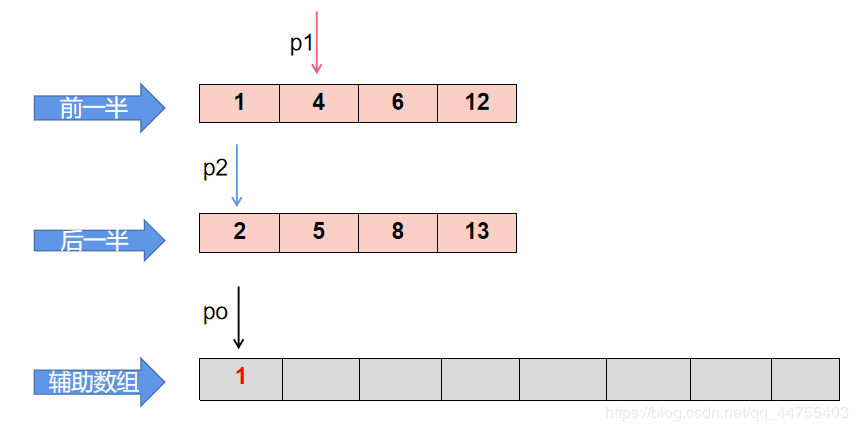重复第 2 步，直至放完一个数组。
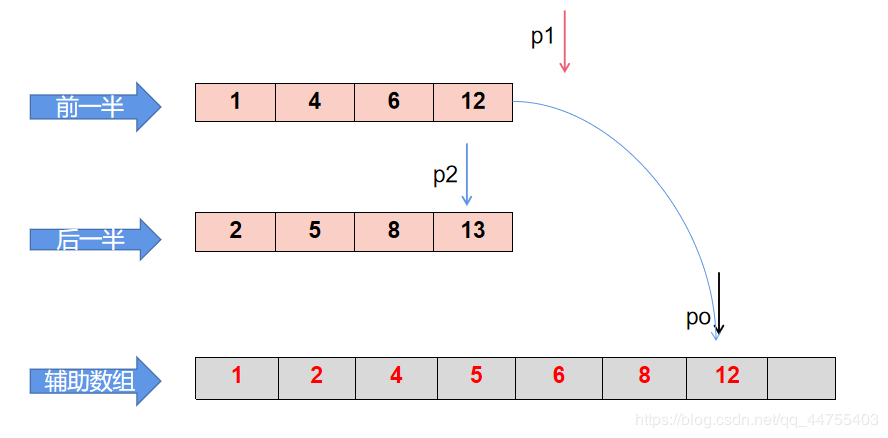这时，前一半数组已经全部放入辅助数组，只需将后一半数组剩余的元素直接填入辅助数组后面即可。
最后将辅助数组的内容拷贝给原始数组即可。注意：不能直接用扫一遍数组进行简单的拷贝，因为每次拷到原始数组的位置都会发生变化，因为它是一个递归的过程。
C++实现：
#include
using namespace std;
void Merge(int *A,int s,int mid,int e,int *T)
{
int po = 0;//指向T数组的第一个
int p1=s, p2=mid+1;//分别指向数组前后两个部分
while (p1 <= mid && p2 <= e)
{
if (A[p1] < A[p2])
{
T[po++] = A[p1++];
}
else
{
T[po++] = A[p2++];
}
}
while (p1 <= mid)
{
T[po++] = A[p1++];
}
while (p2 <= e)
{
T[po++] = A[p2++];
}
for (int i = 0; i < e-s+1; i++)//将归并之后的数组拷贝给原数组
{
A[i+s] = T[i];
}
}
void MergeSort(int *A,int s,int e,int *T)//递归进行归并排序，T为辅助数组
{
if (s < e)
{
int mid = s + (e-s) / 2;
MergeSort(A,s, mid,T);//排序前半部分
MergeSort(A,mid + 1,e,T);//后半部分
Merge(A,s, mid, e,T);//两个部分归并到一起
}
}
int main()
{
int n;
int i;
int A[8] = { 3,0,4,1,7,8,5,2};
n = sizeof(A) / sizeof(int);
int Temp[10] = { 0 };
MergeSort(A,0, n - 1,Temp);
for (i = 0; i < n; i++)
{
cout << A[i]<<" ";
}
cout << endl;
return 0;
}
输出：
0 1 2 3 4 5 7 8
Java实现：
package lu;
public class Test1 {
public static void main(String[] args) {
int n;
int i;
int []A = { 3,0,4,1,7,8,5,2};
n = A.length;
int []Temp = { 0,0,0,0,0,0,0,0 };
MergeSort(A,0, n - 1,Temp);
for (i = 0; i < n; i++)
{
System.out.println(A[i]);
};
}
public static void Merge(int A[],int s,int mid,int e,int T[])
{
int po = 0;//指向T数组的第一个
int p1=s, p2=mid+1;//分别指向数组前后两个部分
while (p1 <= mid && p2 <= e)
{
if (A[p1] < A[p2])
{
T[po++] = A[p1++];
}
else
{
T[po++] = A[p2++];
}
}
while (p1 <= mid)
{
T[po++] = A[p1++];
}
while (p2 <= e)
{
T[po++] = A[p2++];
}
for (int i = 0; i < e-s+1; i++)//将归并之后的数组拷贝给原数组
{
A[i+s] = T[i];
}
}
public static void MergeSort(int []A,int s,int e,int []T)//递归进行归并排序，T为辅助数组
{
if (s < e)
{
int mid = s + (e-s) / 2;
MergeSort(A,s, mid,T);//排序前半部分
MergeSort(A,mid + 1,e,T);//后半部分
Merge(A,s, mid, e,T);//两个部分归并到一起
}
}
}
博客主页
作者：编程之美，趋之若鹜
