数据结构笔记：归并排序

Liana ·

更新时间:2024-11-10

· 599 次阅读

原文地址

分类目录——数据结构笔记

先把整个序列对半拆分，然后对子序列在进行对半拆分，直直拆成每个子序列只有一个元素，

然后再按拆分顺序一层一层反向合并，在拆分过程中原来在一个子序列的，合并后还在子序列，合并时需要保证按序合并

最底层的合并好说，两个值，比较大小，小值在前

再往上，需要为合并的两个子序列配置两个指针（姑且称之为left和right），初始分别指向序列的起始位置，较两个指针指向值，取较小值加入合并序列，较小值指针后移，再比较、加入较小值、较小值指针后移……直到合并完成

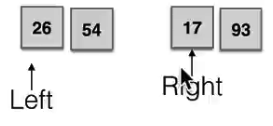
1582857958691

一层层的向上合并，直到将整个序列归并结束

实现

def mergesort(alist):
    n = len(alist)
    # 如果切分到最后一个，直接返回
    if n<=1:
        return alist
    mid = n//2  # 取整除
    # 获得左半部分和有半部分的合并结果
    sub_left = mergesort(alist[:mid])
    sub_right = mergesort(alist[mid:])
    # 定义左右指针
    left_pointer, right_pointer = 0, 0
    # 初始化本轮的归并结果
    result = []
    # 利用两个指针归并当前两个左右子序列
    while left_pointer<len(sub_left) and right_pointer<len(sub_right):
        if sub_left[left_pointer] < sub_right[right_pointer]:
            result.append(sub_left[left_pointer])
            left_pointer += 1
        else:
            result.append(sub_right[right_pointer])
            right_pointer += 1
    # 其中一个指针到头之后（pointer指在最后，[pointer:]就是一个空列表），
    # 将另一个子序列的剩余部分加到结果中
    result += sub_left[left_pointer:]
    result += sub_right[right_pointer:]
    return result

时间复杂度

最优时间复杂度：O(nlogn) 最坏时间复杂度：O(nlogn) 稳定性：稳定

会有比较大的空间复杂度开销

作者：BBJG_001

数据归并排序排序数据结构

1024 个赞