排序算法(二)希尔排序+归并排序+快速排序+堆排序--O(nlogn)的排序
文章目录希尔排序归并排序快速排序(20世纪对世界影响最大的算法之一)牛掰!堆排序
希尔排序
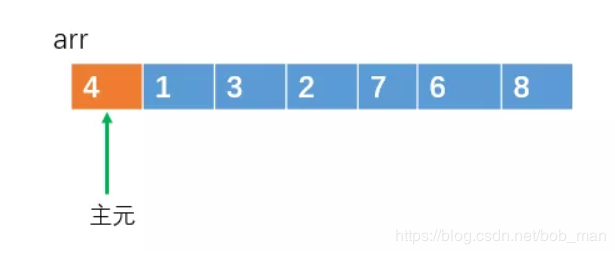
给出一张图,可以结合上面的过程,自己动态得画一画这个排序得过程,立马就明白了,下面给出具体代码,如果还不是很明白,该部分末尾有一篇很优质得文章推荐。
最后,附上一张图作为总结:
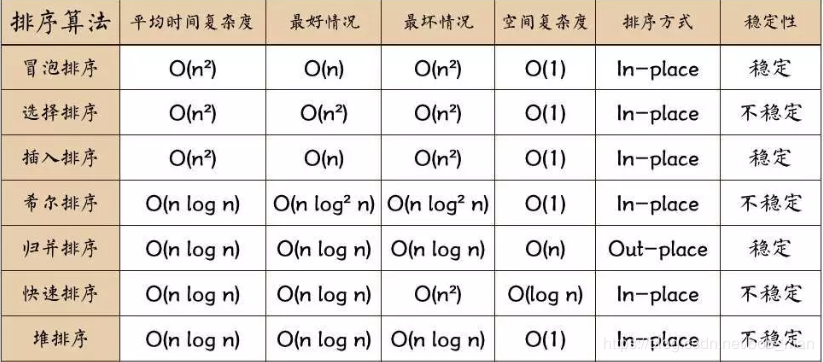
作者:bob_man
排序思想:希尔排序可以说是插入排序的一种变种。无论是插入排序还是冒泡排序,如果数组的最大值刚好是在第一位,要将它挪到正确的位置就需要 n - 1 次移动。当原数组的一个元素如果距离它正确的位置很远的话,需要与相邻元素交换多次才能到达正确的位置,这样效率较低。希尔排序就是插入排序排序的一种简单改进,交换不相邻的元素以对数组的局部进行排序,以此来提升效率。
排序过程:
先让数组中任意间隔为 h 的元素有序,刚开始 h 的大小可以是 h = n / 2 接着让 h = n / 4,让 h 一直缩小,相当于不断增大步长,当 h = 1 时,也就是此时数组中任意间隔为1的元素有序,此时的数组就是有序的了。package sorting;
import java.util.Scanner;
/**
* @ClassName HillSort.java
* @Description 希尔排序
* @Author ZBW
* @Date 2020年03月07日 19:20
**/
public class HillSort {
public static int[] sort(int array[]) {
if (array == null || array.length 0; h /= 2) {
//对各个局部分组进行插入排序
for (int i = h; i 0 && temp < array[k]; k -= h) {
array[k + h] = array[k];
}
array[k + h] = temp;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("请输入待排序数据个数:");
//输入需要排序的数据个数
int n = in.nextInt();
int[] array = new int[n];
System.out.println("请输入待排序数据:");
for (int i = 0; i < n; i++) {
array[i] = in.nextInt();
}
int[] res = sort(array);
print(res);
}
public static void print(int[] array) {
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
}
}
时间复杂度为O(nlogn),空间复杂度:O(1)
属于非稳定排序
属于原地排序
归并排序
排序思想:将一个大的无序数组有序,我们可以把大的数组分成两个,然后对这两个数组分别进行排序,之后在把这两个数组合并成一个有序的数组。由于两个小的数组都是有序的,所以在合并的时候是很快的。
注意:在一个归并排序中,可以将总的数组中n个元素分成logn个层次,每个层次的合并保持在O(n)的复杂度,那么最后的算法时间复杂度为O(nlogn)
排序过程:
通过递归的方式将大的数组一直分割,直到数组的大小为 1,此时只有一个元素,那么该数组就是有序的了 再把两个数组大小为1的合并成一个大小为2的,再把两个大小为2的合并成4的 … 直到全部小的数组合并起来。package sorting;
import java.util.Scanner;
/**
* @ClassName MergeSort.java
* @Description 归并排序递归版本
* @Author ZBW
* @Date 2020年03月07日 22:18
**/
public class MergeSort {
private static int[] sort(int[] array) {
merge(array, 0, array.length - 1);
return array;
}
//递归使用归并排序,对array[l...r]的范围进行排序
private static void merge(int[] array, int l, int r){
if (l >= r) {
return;
}
int mid = (l + r)/2;
merge(array, l, mid);
merge(array, mid + 1, r);
//此处是一种优化,对于整体数组基本有序时的优化
if (array[mid] > array[mid+1]) {
mergeAll(array, l, mid, r);
}
}
//将array[l...mid]和array[mid+1...r]两部分进行归并
private static void mergeAll(int[] array, int l, int mid, int r) {
int[] temp = new int[r-l+1];
for (int i = l; i <= r; i++) {
temp[i-l] = array[i];
}
int i = l, j = mid+1;
for (int k = l; k mid) {
array[k] = temp[j-l];
j++;
} else if (j > r) {
array[k] = temp[i-l];
i++;
} else if (temp[i-l] < temp[j-l]) {
array[k] = temp[i-l];
i++;
} else {
array[k] = temp[j-l];
j++;
}
}
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("请输入待排序数据个数:");
//输入需要排序的数据个数
int n = in.nextInt();
int[] array = new int[n];
System.out.println("请输入待排序数据:");
for (int i = 0; i < n; i++) {
array[i] = in.nextInt();
}
int[] res = sort(array);
print(res);
}
public static void print(int[] array) {
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
}
}
分析上面的sort()函数,时间复杂度为O(nlogn),空间复杂度为O(n)
属于稳定排序
属于非原地排序
上面的是递归版本,下面的是使用迭代进行归并排序的版本:
package sorting;
import java.util.Scanner;
/**
* @ClassName MergeSort2.java
* @Description //TODO
* @Author ZBW
* @Date 2020年03月08日 20:53
**/
public class MergeSort2 {
public static int[] sort(int[] array) {
for (int size = 1; size <= array.length; size += size) {
for (int i = 0; i < array.length; i += size + size) {
mergeAll(array, i, i+size-1, Math.min(i+size+size-1, array.length-1));
}
}
return array;
}
private static void mergeAll(int[] array, int l, int mid, int r) {
int[] temp = new int[r-l+1];
for (int i = l; i <= r; i++) {
temp[i-l] = array[i];
}
int i = l, j = mid+1;
for (int k = l; k mid) {
array[k] = temp[j-l];
j++;
} else if (j > r) {
array[k] = temp[i-l];
i++;
} else if (temp[i-l] < temp[j-l]) {
array[k] = temp[i-l];
i++;
} else {
array[k] = temp[j-l];
j++;
}
}
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("请输入待排序数据个数:");
//输入需要排序的数据个数
int n = in.nextInt();
int[] array = new int[n];
System.out.println("请输入待排序数据:");
for (int i = 0; i < n; i++) {
array[i] = in.nextInt();
}
int[] res = sort(array);
print(res);
}
public static void print(int[] array) {
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
}
}
快速排序(20世纪对世界影响最大的算法之一)牛掰!
排序思路:
首先我们来看总体的排序过程
注意:
快排中最核心的部分就是划分的partition过程,而且是需要借助外部空间的 快速排序中partition时主元的选取可以是任意的,不一定必须是第一个元素为主元,可以选取第一个或者最后一个,也可以利用random随机生成介于0到数组长度之间的一个整数作为主元索引,将对应元素作为主元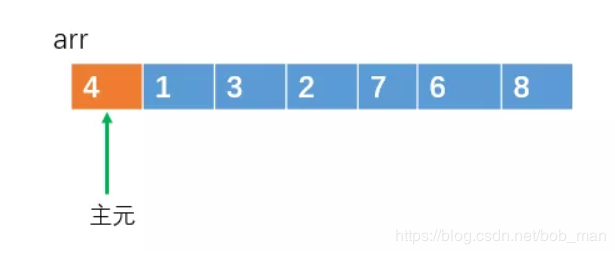
给出一张图,可以结合上面的过程,自己动态得画一画这个排序得过程,立马就明白了,下面给出具体代码,如果还不是很明白,该部分末尾有一篇很优质得文章推荐。
package sorting;
import java.util.Scanner;
/**
* @ClassName QuickSort.java
* @Description 快速排序
* @Author ZBW
* @Date 2020年03月07日 22:20
**/
public class QuickSort {
private static int[] sort(int[] array) {
quickSort(array, 0, array.length-1);
return array;
}
//对于arr[l....r]部分进行排序
private static void quickSort(int[] array, int l, int r) {
if (l >= r) {
return;
}
int p = partition(array, l, r);
quickSort(array, l, p-1);
quickSort(array, p+1, r);
}
//对array[l...r]部分进行partition操作
//返回p,使得array[l...p-1] arr[p]
//partition过程也是整个排序算法最为核心的部分
private static int partition(int[] array, int l, int r) {
int v = array[l];
int i = l + 1, j = r;
while (true) {
//i向右遍历过程,如果比主元大就停止
while (i <= j && array[i] <= v) {
i++;
}
//j向左遍历过程,如果比主元小就停止
while (i = v) {
j--;
}
if (i >= j) {
break;
}
//对二者进行交换
int temp = array[j];
array[j] = array[i];
array[i] = temp;
}
//将arr[j]和主元继进行交换,这样主元之前的元素都小于主元,主元后的元素都大于主元
array[l] = array[j];
array[j] = v;
return j;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("请输入待排序数据个数:");
//输入需要排序的数据个数
int n = in.nextInt();
int[] array = new int[n];
System.out.println("请输入待排序数据:");
for (int i = 0; i < n; i++) {
array[i] = in.nextInt();
}
int[] res = sort(array);
print(res);
}
public static void print(int[] array) {
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
}
}
优质文章推荐:别再问我快速排序了
观察上面的排序过程,时间复杂度为O(nlogn),空间复杂度为O(logn) 属于非稳定排序 属于原地排序补充:
当选定第一个元素为主元时,当数组基本有序时,每次只会对主元一边的数组进行分割,这样,分割次数会边多,而算法的时间复杂度会退化为O(n2),但是当对主元进行随机选取的时候,就不一样了,它的时间复杂度的期望值就是**O(logn)了,但是注意,只是期望,就是说快速排序退化成O(n2)**复杂度的概率就很低了,上面的代码在这方面也可以进行优化 当一个数组中,有很多重复元素,partition操作都容易将数组划分为极度不平衡的两部分,即使我们的主元选择得很合适,这时候复杂度也会退化为**O(n2)**的复杂度,上面的是已经进行优化过的版本 当然,提到了上面的问题,对于大量重复元素存在于数组中的情况,还可以进行三路快速排序,将整个数组划分为小于主元,等于主元,大于主元三部分区域 堆排序堆:对应的应该是一个树形结构,比如二叉堆
堆排序:堆排序就是把堆顶的元素与最后一个元素交换,交换之后破坏了堆的特性,我们再把堆中剩余的元素再次构成一个大顶堆,然后再把堆顶元素与最后第二个元素交换….如此往复下去,等到剩余的元素只有一个的时候,此时的数组就是有序的了。
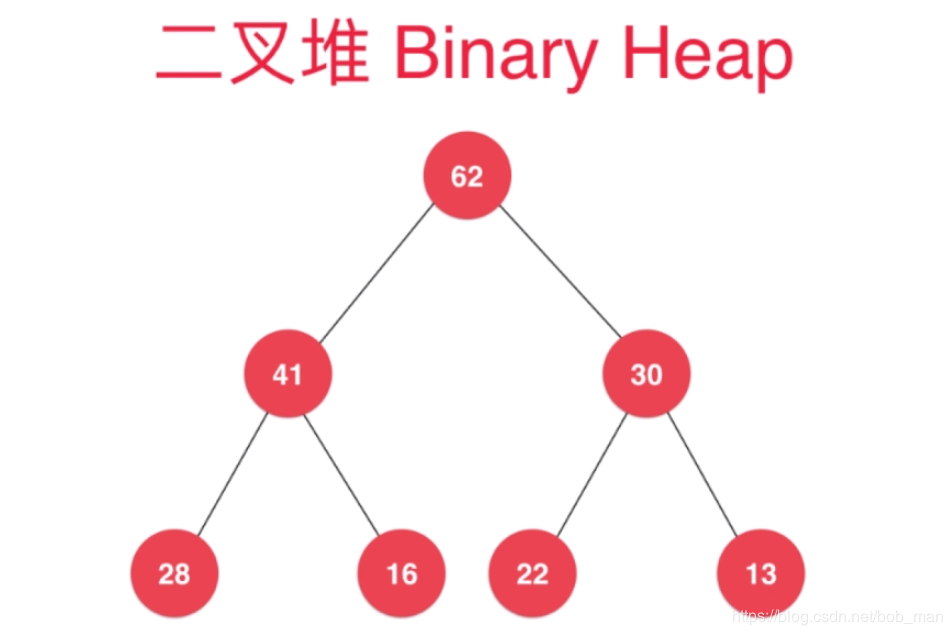
二叉堆是一颗完全二叉树,在堆中某个节点的值总是不大于其父节点的值,堆总是一颗完全二叉树(最大堆),最小堆与之同理
package sorting;
import java.util.Arrays;
import java.util.Scanner;
/**
* @ClassName HeapSort.java
* @Description 堆排序
* @Author ZBW
* @Date 2020年03月15日 22:21
**/
public class HeapSort {
/**
* 下沉操作,执行删除操作相当于把最后
* 一个元素赋给根元素之后,然后对根元素执行下沉操作
*/
public static int[] downAdjust(int[] arr, int parent, int length) {
//临时保证要下沉的元素
int temp = arr[parent];
//定位左孩子节点位置
int child = 2 * parent + 1;
//开始下沉
while (child < length) {
//如果右孩子节点比左孩子小,则定位到右孩子
if (child + 1 arr[child + 1]) {
child++;
}
//如果父节点比孩子节点小或等于,则下沉结束
if (temp = 0; i--) {
arr = downAdjust(arr, i, length);
}
//进行堆排序
for (int i = length - 1; i >= 1; i--) {
//把堆顶的元素与最后一个元素交换
int temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
//下沉调整
arr = downAdjust(arr, 0, i);
}
return arr;
}
//测试
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("请输入待排序数据个数:");
//输入需要排序的数据个数
int n = in.nextInt();
int[] array = new int[n];
System.out.println("请输入待排序数据:");
for (int i = 0; i < n; i++) {
array[i] = in.nextInt();
}
array = heapSort(array, array.length);
System.out.println(Arrays.toString(array));
}
}
堆排序的时间复杂度为O(nlogn),空间复杂度为O(1)
属于非稳定排序
属于原地排序最后,附上一张图作为总结:

作者:bob_man
相关文章
Xena
2020-07-03
Serafina
2021-03-06
Liana
2021-04-13
Wenda
2020-04-23
Helena
2020-06-23
Violet
2020-05-15
Badia
2021-05-01
Victoria
2023-07-17
Liana
2023-07-20
Trixie
2023-07-20
Hester
2023-07-20
Ianthe
2023-07-20
Valora
2023-07-20
Jacinda
2023-07-20
Winola
2023-07-20
Emily
2023-07-20
Radinka
2023-07-20
Gella
2023-07-20
Tertia
2023-07-21
Diane
2023-08-28