数据库2_3——关系代数
【这个行与列的区别需要好好斟酌】 运算符
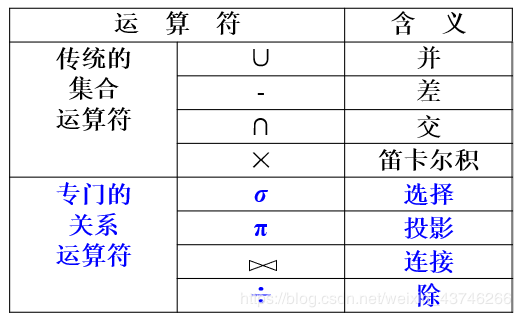
传统的集合运算不细讲，并（union）与交（intersection），高中老朋友了，讲一下差（difference）和笛卡尔积（Cartesian Product）吧！
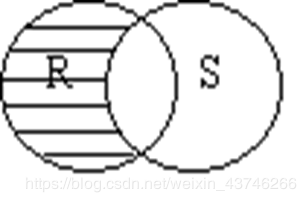
差R - S : 由属于R而不属于S的所有元组组成,R−S={t∣t∈R∩t∉S}R - S = \{ t|t\in R \cap t\notin S \}R−S={t∣t∈R∩t∈/S} R,S具有相同的目n R,S相应的属性取自同一个域
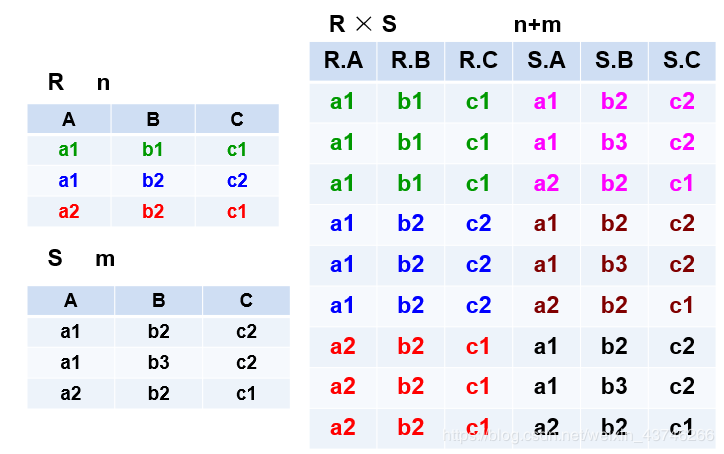
笛卡尔积 (文字不用看，直接看图）R: n目关系，k1个元组
S: m目关系，k2个元组
R×S
列：（n+m）列元组的集合
(1)元组的前n列是关系R的一个元组
(2)后m列是关系S的一个元组
行：k1×k2个元组
3. 专门的关系运算
记号的引入
R，t∈R，t[Ai]R，t\in R，t[Ai]R，t∈R，t[Ai]
(1)设关系模式为R(A1，A2，…，An)
它的一个关系设为R
(2) t∈Rt\in Rt∈R表示t是关系R的一个元组
(3) t[Ai]t[Ai]t[Ai] 则表示元组t中相应于属性Ai的一个分量
A，t[A]，AˉA，t[A]， \bar AA，t[A]，Aˉ
（1）若A={Ai1，Ai2，…，Aik}A=\{Ai1，Ai2，…，Aik\}A={Ai1，Ai2，…，Aik}，其中Ai1，Ai2，…，AikAi1，Ai2，…，AikAi1，Ai2，…，Aik是A1，A2，…，AnA1，A2，…，AnA1，A2，…，An中的一部分，则A称为属性列或属性组。
（2）t[A]=(t[Ai1]，t[Ai2]，…，t[Aik])t[A]=(t[Ai1]，t[Ai2]，…，t[Aik])t[A]=(t[Ai1]，t[Ai2]，…，t[Aik])表示元组t在属性列A上诸分量的集合。
（3）Aˉ\bar AAˉ则表示{A1，A2，…，An}\{A1，A2，…，An\}{A1，A2，…，An}中去掉{Ai1，Ai2，…，Aik}\{Ai1，Ai2，…，Aik\}{Ai1，Ai2，…，Aik}后剩余的属性组。
trts⌢\overset{\frown}{t_{r}t_{s}}trts⌢
R为n目关系，S为m目关系。
tr∈R，ts∈S，trts⌢t_{r}\in R，t_{s}\in S，\overset{\frown}{t_{r}t_{s}}tr∈R，ts∈S，trts⌢称为元组的连接。
trts⌢\overset{\frown}{t_{r}t_{s}}trts⌢是一个n+mn + mn+m列的元组，前n个分量为R中的一个n元组，后m个分量为S中的一个m元组
象集ZxZ_{x}Zx
给定一个关系R（X，Z），X和Z为属性组。
当t[X]=x时，x在R中的象集（Images Set）为：Zx={t[Z]∣t∈R，t[X]=x}Zx=\{ t[Z]|t \in R，t[X]=x\}Zx={t[Z]∣t∈R，t[X]=x}
它表示R中属性组X上值为x的诸元组在Z上分量的集合
学生-课程数据库：学生关系Student、课程关系Course、选修关系SC
Student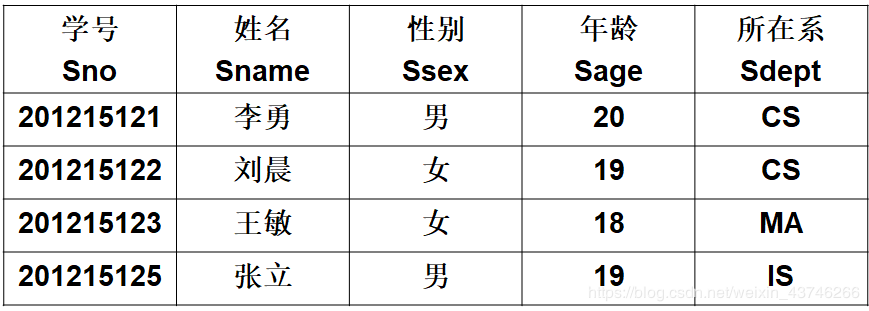
Course
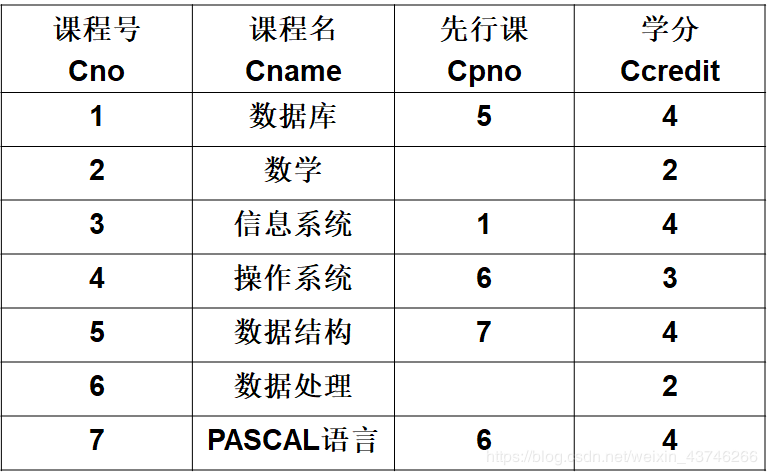SC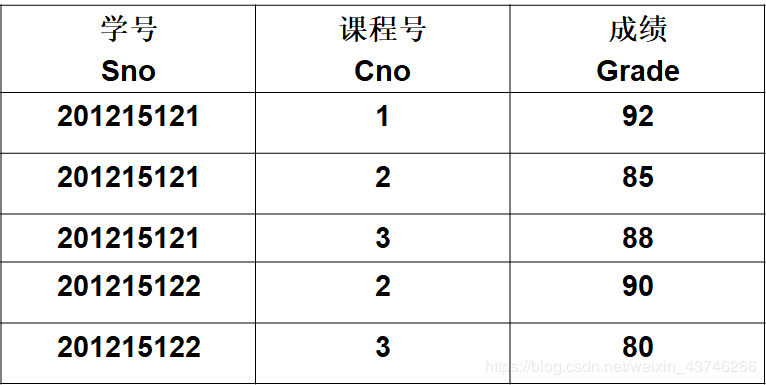
3.1 选择
选择又称为限制（Restriction）
选择运算符的含义在关系R中选择满足给定条件的诸元组
σF(R)={t∣t∈R∩F(t)=真}σ_{F}(R) = \{ t | t\in R\cap F(t)= 真 \}σF(R)={t∣t∈R∩F(t)=真}
F：选择条件，是一个逻辑表达式，取值为“真”或“假”
基本形式为：X1θY1X_{1}θY_{1}X1θY1
θ表示比较运算符，它可以是＞，≥，＜，≤，＝， 选择运算是从关系R中选取使逻辑表达式F为真的元组，是从行的角度进行的运算 例子：σCno=1(SC)σ_{Cno=1}(SC)σCno=1(SC)
3.2 投影（Projection）
从R中选择出若干属性列组成新的关系πA(R)={t[A]∣t∈R}π_{A}(R) = \{ t[A] | t \in R \}πA(R)={t[A]∣t∈R}
A：R中的属性列 投影操作主要是从列的角度进行运算 投影之后不仅取消了原关系中的某些列，而且还可能取消某些元组（避免重复行） 例子：πSname,Sdept(Student)π_{Sname,Sdept}(Student)πSname,Sdept(Student)
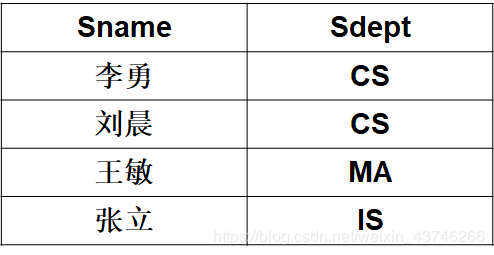3.3 连接(Join)
3.3.1 定义
连接也称为θ连接
连接运算的含义从两个关系的笛卡尔积中选取属性间满足一定条件的元组
R⋈AθBS={trts⌢∣tr∈R∩ts∈S∩tr[A]θts[B]}R\mathop{\bowtie}\limits_{AθB} S = \{ \overset{\frown}{t_{r}t_{s}}|t_{r}\in R\cap t_{s} \in S\cap t_{r}[A]θt_{s}[B] \}RAθB⋈S={trts⌢∣tr∈R∩ts∈S∩tr[A]θts[B]}
（1）A和B：分别为R和S上度数相等且可比的属性组
（2）θ：比较运算符 连接运算从R和S的广义笛卡尔积R×S中选取R关系在A属性组上的值与S关系在B属性组上的值满足比较关系θ的元组 3.3.2 两种常用的连接运算 等值连接（equijoin）
θ为“＝”的连接运算称为等值连接
从关系R与S的广义笛卡尔积中选取A、B属性值相等的那些元组，即等值连接为：R⋈A=BS={trts⌢∣tr∈R∩ts∈S∩tr[A]=ts[B]}R\mathop{\bowtie}\limits_{A=B} S = \{ \overset{\frown}{t_{r}t_{s}}|t_{r}\in R\cap t_{s} \in S\cap t_{r}[A]=t_{s}[B] \}RA=B⋈S={trts⌢∣tr∈R∩ts∈S∩tr[A]=ts[B]} 自然连接（Natural join）
自然连接是一种特殊的等值连接
两个关系中进行比较的分量必须是相同的属性组
在结果中把重复的属性列去掉
自然连接的含义：R和S具有相同的属性组B
R⋈S={trts⌢[U−B]∣tr∈R∩ts∈S∩tr[B]=ts[B]}R\mathop{\bowtie} S = \{ \overset{\frown}{t_{r}t_{s}}[U-B]|t_{r}\in R\cap t_{s} \in S\cap t_{r}[B]=t_{s}[B] \}R⋈S={trts⌢[U−B]∣tr∈R∩ts∈S∩tr[B]=ts[B]} 一般的连接操作是从行的角度进行运算。
自然连接还需要取消重复列，所以是同时从行和列的角度进行运算。 3.3.3 例子
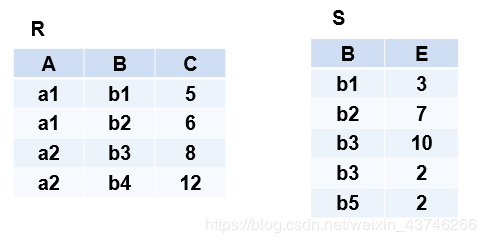
一般链接 ：R⋈C<ESR\mathop{\bowtie}\limits_{C<E} SRC<E⋈S
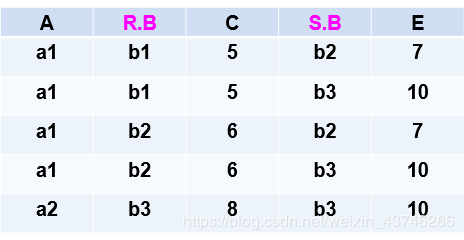
等值连接：R⋈R.B=S.BSR\mathop{\bowtie}\limits_{R.B=S.B} SRR.B=S.B⋈S
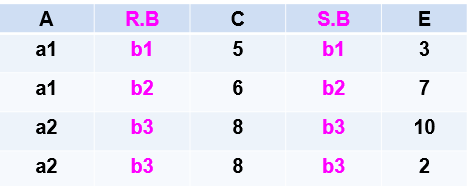
自然连接:R⋈SR\mathop{\bowtie} SR⋈S
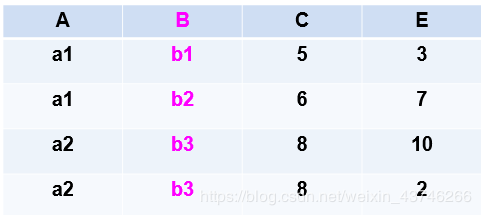
两个关系R和S在做自然连接时，关系R中某些元组有可能在S中不存在公共属性上值相等的元组，从而造成R中这些元组在操作时被舍弃了，这些被舍弃的元组称为悬浮元组。
例如：做自然连接时R的第四个元组，S的第五个元组
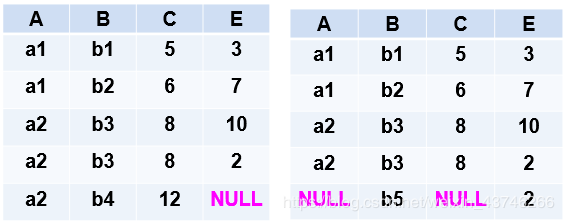
3.3.5 外连接（Outer Join） 如果把悬浮元组也保存在结果关系中，而在其他属性上填空值(Null)，就叫做外连接 左外连接(LEFT OUTER JOIN或LEFT JOIN)：只保留左边关系R中的悬浮元组 右外连接(RIGHT OUTER JOIN或RIGHT JOIN)：只保留右边关系S中的悬浮元组下图分别为左外连接和右外连接：
域集。 R与S的除运算得到一个新的关系P(X)， P是R中满足下列条件的元组在 X 属性列上的投影： 元组在X上分量值x的象集Yx包含S在Y上投影的集合，记作：
R÷S={tr[X]∣tr∈R∧πY(S)⊂Yx}R÷S = \{ t_{r}[X] | t_{r}\in R ∧π_{Y}(S) \subset Yx \}R÷S={tr[X]∣tr∈R∧πY(S)⊂Yx}
Yx：x在R中的象集，x=tr[X]x = t_{r}[X]x=tr[X]
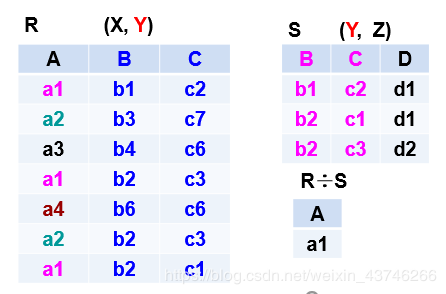
解析： 在关系R中，A可以取四个值{a1，a2，a3，a4}
a1的象集为 {(b1，c2)，(b2，c3)，(b2，c1)}
a2的象集为 {(b3，c7)，(b2，c3)}
a3的象集为 {(b4，c6)}
a4的象集为 {(b6，c6)} S在(B，C)上的投影为
{(b1，c2)，(b2，c1)，(b2，c3) } 只有a1的象集包含了S在(B，C)属性组上的投影
所以 R÷S ={a1} 总结
关系就是表
| 运算 | 符号 | 说明 |
|---|---|---|
| 并 | ∪\cup∪ | 取两个表的并集 |
| 交 | ∩\cap∩ | 取两个表的并集 |
| 差 | −-− | 前表去掉两个表的公共部分 |
| 笛卡尔积 | x | 生成一个a+b行，n*m列的新表（a，b为原来行数，m，n为原来列数） |
| 选择 | σF(R)σ_{F}(R)σF(R) | 去除R中满足关系F的多个元组 |
| 投影 | πA(R)π_{A}(R)πA(R) | 在关系R中取出属性为A的列，去掉重复行 |
| 连接 | R⋈AθBSR\mathop{\bowtie}\limits_{AθB} SRAθB⋈S | 两个集合有可以比较的l两列，然后连两个表1 |
| 除 | ÷ | 我的理解R中 包含 S中 的所有Y 的x |
自然连接时没有重复属性列的等值连接，外连接是补空值的自然连接 ↩︎
作者：必修居士
