关系数据库及关系代数的基本概念
此篇回答的是《数据库原理概论》中第二章的习题
1.定义并理解下列术语,说明他们之间的联系和区别: (1) 域,笛卡儿积,关系,元组,属性;域(domain):域是一组具有相同数据类型的值的集合。
笛卡尔积(cartesian pproduct):笛卡尔积是域上的一种集合运算。
以下三个定义可以可以参见我上次的文章中的第3问。传送门
关系(relation):
元组(tuple):
属性(attribute):
——————————————————————————————————————————
关于笛卡尔积我们来详细讲讲。首先给出定义:
给定一组域D1,D2,···,Dn,允许其中某些域是相同的,D1,D2,···,Dn的笛卡尔积为
D1×D2×···×Dn={(d1,d2,···,dn)| di∈Di,i=1,2,···,n}
其中,每一个元素(d1,d2,···,dn)叫做一个n元组(n-tuple),或简称元组(tuple)。元素中的每一个值di叫做一个分量(component)。
一个域允许的不同取值个数称为这个域的基数(cardinal number)。
若Di(i=1,2,···,n)为有限集,其基数为mi(i=1,2,···,n),则D1×D2×···×Dn的基数M为
M=∏m=0nmi
M=\prod_{m=0}^{n}m_{i}
M=m=0∏nmi
那么这段话是什么意思呢?其实很简单。
我们之前说过,"域"是一种集合,而笛卡尔积也是集合里面的一种概念,同样能够用集合的思想去理解。
所以假设我们有A集合与B集合,其中A={ a , b },B={ 1, 2, 3 } 。
根据定义,我们有A×B={ (a,1),(a,2),(a,3),(b,1),(b,2),(b,3) }。
笛卡尔积就是所有域的所有组合的一个集合(记得要去除相同的域的组合)
说白了就是将两个集合(域)里面的元素相乘。
然后我们就知道,像(a,1),(b,2)这样的叫做元组,因为里面有两个元素(分量),所以我们叫它二元组。A集合的基数为2,B集合的基数为3,A×B的基数则为2×3=6.若是有相同的分量的话则基数应该相应地减去重复分量的值。
——————
刚刚讲的是在集合中的笛卡尔积,那么我们回到关系数据库上。
在关系数据库中,笛卡尔积可以表示一张二维表,表中的每行都是一个元组,表中的每一列的值都是来自一个域,同我在上篇文章中的表述相同。
简单举个例子。给出两个域:
D1=老师集合TEACHER={李老师,王老师}
D2=科目集合SUBJECT={数学,语文}
D3=学生集合PUPIL={李红,张勇}
一对一培训
那我们有笛卡尔积:
D1×D2×D3={
(李老师,数学,李红),(李老师,数学,张勇),
(李老师,语文,李红),(李老师,语文,张勇),
(张老师,数学,李红),(张老师,数学,张勇),
(张老师,语文,李红),(张老师,语文,张勇)}
其中,(李老师,数学,李红)这样的就是元组,,张老师,李老师,数学这样的是分量。同时,该笛卡尔积的基数为2×2×2=8
可以绘制成表格
| TEACHER | SUBJECT | PUPIL |
|---|---|---|
| 李老师 | 数学 | 李红 |
| 李老师 | 数学 | 张勇 |
| 李老师 | 语文 | 李红 |
| 李老师 | 语文 | 张勇 |
| 张老师 | 数学 | 李红 |
| 张老师 | 数学 | 张勇 |
| 张老师 | 语文 | 李红 |
| 张老师 | 语文 | 张勇 |
对于关系(relation)我在这里再补充下在关系数据库中的定义。
D1×D2×···×Dn 的子集叫做在域D1,D2,···,Dn 上的关系,表示为R(D1,D2,···,Dn)
这里R表示关系的名字,n是关系的目或者度(degree)。
如上表中R为TSP(TEACHER,SUBJECT,PUPIL),n=3;
——————————————————————————————————————————
(2) 主码,候选码,外码; 候选码(candidate key):若关系中的某一属性组的值能唯一地标识一个元组,而其子集不能,则称该属性组为候选码(candidate key)。
主码(primary key):若一个关系有多个候选码,则选定其中一个为主码(primary key)。
外码(foreign key):设F是基本关系R的一个或一组属性,但不是关系R的码,Ks是基本关系S的主码。如果F与Ks相对应,则称F是R的外码(foreign key),并称基本关系R为参照关系(referencing relation),基本关系S为被参照关系(referenced relation) 或目标关系(target relation)。关系R和S不一定是不同的关系。
此处候选码的意思就是该列的值都都能确定一个元组。我之前的那个表格不适合确定候选码,我们可以回想学生信息表里面的学号,是每个学生都独一无二的。假若学校里的人都不重名,那么学生信息表内的候选码就有俩——学号和姓名。然后你可以随便选定一个候选码作为主码。若所有属性都是候选码,那么则称为全码(all-key)。
至于外码,简单上个图:
(图片来自Jaihk662的博客)
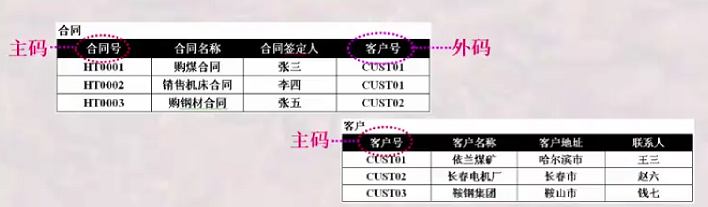
简单来说,对于图中的第一个关系,"客户号"并不是候选码或者主码,但它在第二个关系中是主码,使得两种关系构成了某种映射。这个属性就像桥梁一样沟通了两段关系,我们愿称之为外码。
当然它也可以是在同一个关系中的一种联系,比如学生信息中可以有一个属性叫班长,班长的值就是班长的学号,连接到了"学号“这一属性。这样也可以叫做外码。
关系模式(relation schema):关系的描述称为关系模式。它可以形式化地表示为R(U,D,DOM,F)
其中R为关系名,U为组成该关系的属性名集合,D为U中属性所来自的域,DOM为属性向域的映像集合,F为属性间数据的依赖关系集合。
一般可以简记为R(U)或R(A1,A2,···,An) 其中R为关系名,A1,A2,···,An为属性名。
关系(relation):参照前文中的补充定义。
关系数据库:在一个给定的应用领域中,所有关系的集合构成一个关系数据库。关系数据库的型也称为关系数据库模式,是对关系数据库的描述。关系数据库的值是这些关系模式在某一时刻对应的关系的集合,通常就称为关系数据库。
关系模型和关系在我上次的文章(传送门在文章开头)和上文中有了较为详细的解释,此处不再赘述。那么对于新概念——关系数据库我们是怎么解释呢?又拿学生信息表来说,因为目前只需要这么一张表,所以这么一张表所构成的一个集合就是关系数据库。

—————————————————————————
2、试述关系模型的完整性规则。在参照完整性中,什么情况下外码属性的值可以为空值? 关系模型中有三类完整性约束:实体完整性(entity integrity)、参照完整性(referential integrity)和用户定义的完整性(user-defined integrity)。实体完整性简单来说就是主码不能为空;参照完整性指的是外码要么为空,要么源自被参照关系的主码,当该外码在第一段关系中不是主属性的时候可以取空值;用户定义完整性指的是针对某一具体关系数据库的约束条件,反映某一具体应用所涉及的数据必须满足语义要求(也就是根据问题的实际情况,对数据有不同的要求。例如0.5个人这种说法,它可能在数学上是存在的,但它不符合语义,违背了用户定义完整性。
—————————————————————————

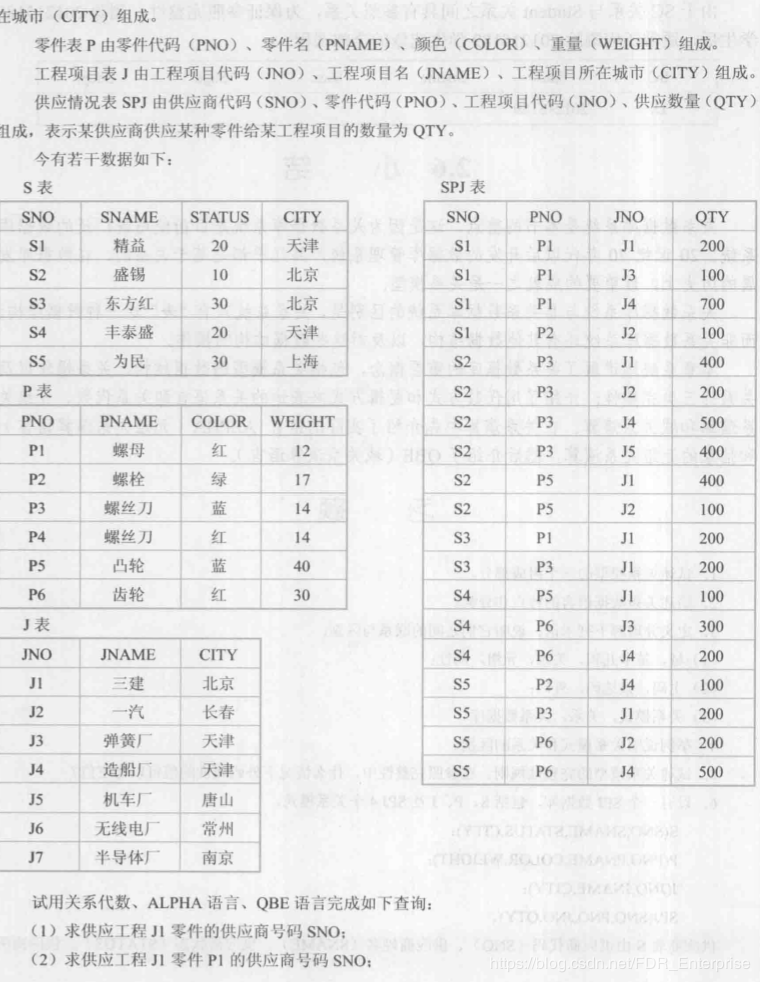

详细的关系代数概念还待施工~没时间了
这一题我们用关系代数来完成查询。因为另外两个都没有学
ΠSNO(σJNO=′J1′(SPJ))\Pi_{SNO}(\sigma_{JNO='J1'}(SPJ))ΠSNO(σJNO=′J1′(SPJ))
思路:J1在J表和SPJ表中出现,SNO出现在SPJ表中,仔细看J表和题目 没有关系,所以主要在J表中寻找。读题目可以知道这是一种投影(查某属性的统一元组中的另一个属性的值),所以外层用投影,内层用选择。
ΠSNO(σJNO=′j1′∧PNO=′P1′(SPJ))\Pi_{SNO}(\sigma_{JNO='j1'\wedge PNO='P1'}(SPJ)) ΠSNO(σJNO=′j1′∧PNO=′P1′(SPJ))
思路:和上一题基本一样,只是多加了一个属性。
ΠSNO(ΠSNO,PNO(σJNO=′J1′(SPJ))⋈ΠPNO(σCOLOR=′红′(P)))\Pi_{SNO}(\Pi_{SNO,PNO}(\sigma_{JNO='J1'}(SPJ))\Join\Pi_{PNO}(\sigma_{COLOR='红'}(P))) ΠSNO(ΠSNO,PNO(σJNO=′J1′(SPJ))⋈ΠPNO(σCOLOR=′红′(P)))
思路:这个稍微复杂一点。我们可以看到主要涉及的表有P表和SPJ表,针对颜色,我们可以先把P表中红色的零件的PNO都选出来,就是连接符号的后面一段。然后再把JNO='J1’的从SPJ表中投影出来他们的SNO和PNO,接着和我们得到的红色零件的PNO连接,就可以得到问题的答案。
ΠJNO(SPJ)−ΠJNO(σCITY=′天津′∧COLOR=′红′(S⋈SPJ⋈P)\Pi_{JNO}(SPJ)-\Pi_{JNO}(\sigma_{CITY='天津' \wedge COLOR='红'} (S\Join SPJ\Join P)ΠJNO(SPJ)−ΠJNO(σCITY=′天津′∧COLOR=′红′(S⋈SPJ⋈P)
思路:先选出SPJ表内使用了天津供应商和红色零件的JNO,做到这一点需要连接S表和P表。再拿整个SPJ表中的JNO减去这些就是问题所求。
ΠJNO,PNO(SPJ)÷ΠPNO(σSNO=′S1′(SPJ))\Pi_{JNO,PNO}(SPJ)\div \Pi_{PNO}(\sigma_{SNO='S1'}(SPJ))ΠJNO,PNO(SPJ)÷ΠPNO(σSNO=′S1′(SPJ))
思路:可以先自己想想