数据库关系代数中的一些定义名词的个人理解
1、
（1）先说关系，关系可以理解为一张表。元组则是这张表（关系）中的一行；属性则是这张表中的一列。域是有相同数据类型值的集合，类似于表中某个属性的并集。笛卡尔积则是在域上的一种集合运算。
（2）若关系中的某一属性组的值能够唯一地标识一个元组，则称该属性组为候选码，从候选码中选定的一个码为主码；如果一个属性在表（关系）中既不是主码也不是候选码，但是他是另一个关系的主码那它就是外码。
（3）关系是一张表。关系模式是对这张表的属性或者其他之间联系的描述；关系数据库是若干张表的集合。
2、
实体完整性：所谓的实体完整性就是指关系(表)的主码不能取空值；比如学生表的主码通常是取学号为主码。
参照完整性：是指参照关系中每个元素的外码要么为空，要么等于被参照关系中某个元素的主码；比如新进大学的同学未分配专业，则其专业属性未空，而等到其分配专业的时候，其分配的专业是唯一的。
用户定义的完整性：指对关系中每个属性的取值作一个限制的具体定义。比如 性别属性只能取”男“或”女“ 。
需要注意的是，当前表中任何外码都不为其他关系的主码时可为空，若为其他关系的主码则一定不能为空。
3、
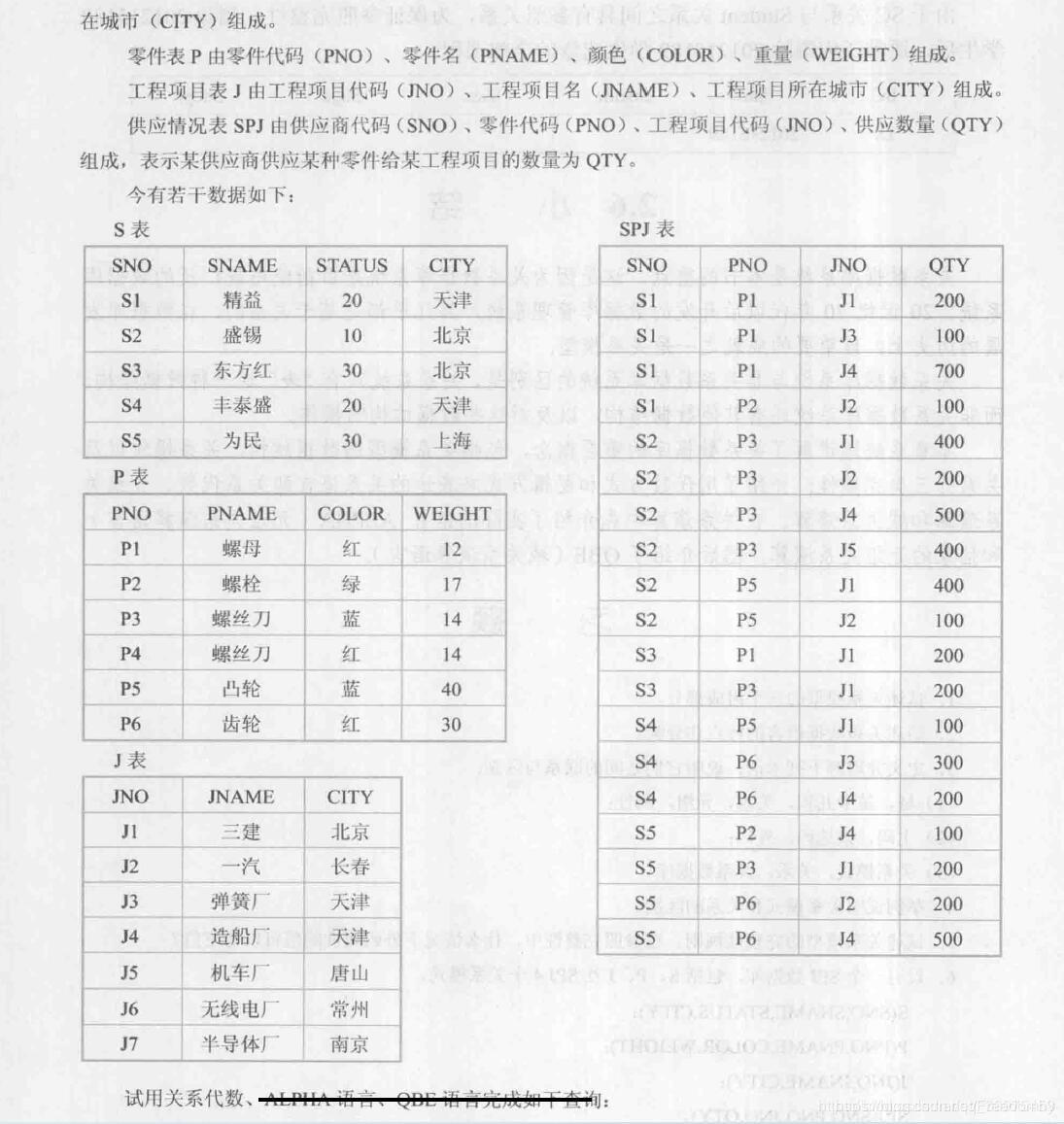
（1）ΠSNO(σJNO=′J1′(SPJ))\Pi_{S N O}\left(\sigma_{J N O=^{\prime} J 1^{\prime}}(S P J)\right)ΠSNO(σJNO=′J1′(SPJ))
（2）ΠSNO(σJNO=′J1′∧PNO=P1′(SPJ))\Pi_{S N O}\left(\sigma_{J N O=^{\prime} J 1^{\prime} \wedge P N O=P 1^{\prime}}(S P J)\right)ΠSNO(σJNO=′J1′∧PNO=P1′(SPJ))
（3）ΠSNO(ΠSNO,PNO(σJNO=J1′(SPJ)⋈ΠPNO(σCOLOR=′红‾′(P)))\Pi_{S N O}\left(\Pi_{S N O, P N O}\left(\sigma_{J N O=J 1^{\prime}}(S P J) \bowtie \Pi_{P N O}\left(\sigma_{C O L O R=^{\prime} \underline{红}^{\prime}}(P)\right)\right)\right.ΠSNO(ΠSNO,PNO(σJNO=J1′(SPJ)⋈ΠPNO(σCOLOR=′红′(P)))
（4）ΠJNO(SPJ)—ΠJNO(σCITY=′天津′∧COLOR=′红色′(S⋈SPJ⋈P))\Pi_{J N O}(S P J)—\Pi_{J N O}\left(\sigma_{C I T Y=^{\prime}天津^{\prime}\wedge C O L O R=^{\prime}红色^{\prime}} (S \bowtie S P J \bowtie P)\right)ΠJNO(SPJ)—ΠJNO(σCITY=′天津′∧COLOR=′红色′(S⋈SPJ⋈P))
（5）ΠJNO,PNO(SPJ)÷ΠPNO(σSNO=′S1′(SPJ))\Pi_{J N O, P N O}(S P J) \div \Pi_{P N O}\left(\sigma_{S N O=^{\prime} S 1^{\prime}}(S P J)\right)ΠJNO,PNO(SPJ)÷ΠPNO(σSNO=′S1′(SPJ))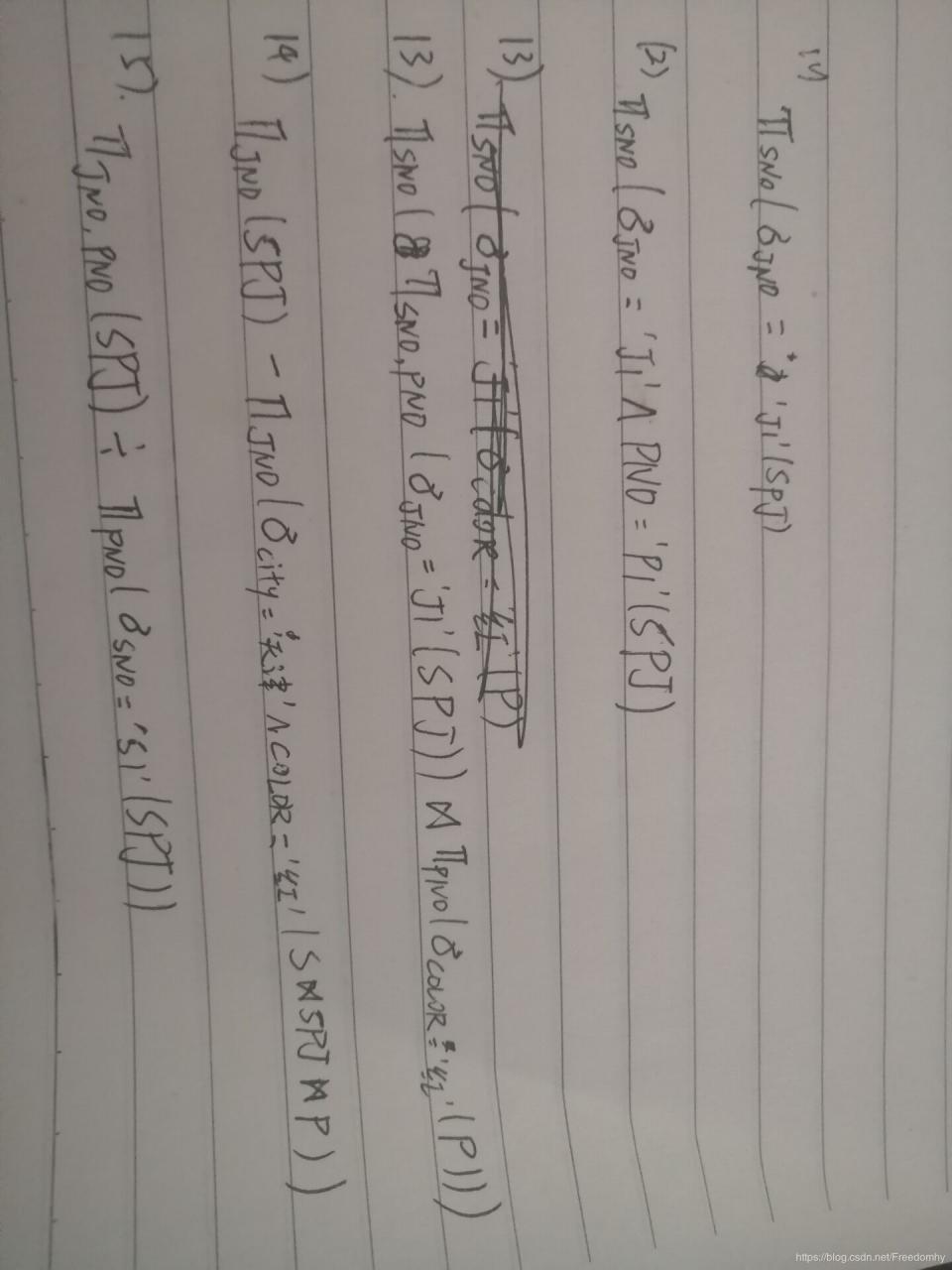
4、并、差、笛卡尔积、投影和选择5种运算为基本的运算。其他3种运算，即交、连接和除，均可以用这5种基本运算来表达。
作者：Freedomhy
