Python+OpenCV 实现简单的高斯滤波(推荐)
基本原理讲解:高斯模糊的算法
高斯核函数的编写:构建权重矩阵,采用高斯二维分布函数的形式进行处理。需要注意的是,这里我没有特判当sigma = 0的时候的情况。
即是实现:
1)权重矩阵的构建
根据公式:
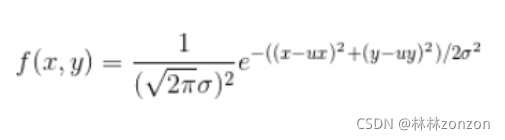
计算矩阵内部结构,其中因为要进行归一化处理,e前方的系数会被约去,因此代码中不体现。
2)矩阵元素归一化处理
计算矩阵内部元素总和sum,最后做矩阵除法得到归一化处理后的权重矩阵。
# 高斯核生成函数 kernel_size:滤波核大小 sigma:高斯核函数的局部影响范围
def gauss(kernel_size, sigma):
#定型0填充
kernel = np.zeros((kernel_size, kernel_size))
#确定正态分布中间值
center = kernel_size // 2
# s:方差 sum:记录总和
s = sigma ** 2
sum = 0
for i in range(kernel_size):
for j in range(kernel_size):
#由于最后要进行归一化处理,此处根号下2Π计算可以省略
x, y = i - center, j - center
kernel[i, j] = np.exp(-(x ** 2 + y ** 2) / (2 * s))
sum += kernel[i, j]
#归一化处理后输出
kernel = kernel / sum
return kernel
滤波函数的编写:将图片中的每个像素点(边缘除外)及其周围像素乘以权重矩阵,实现高斯滤波
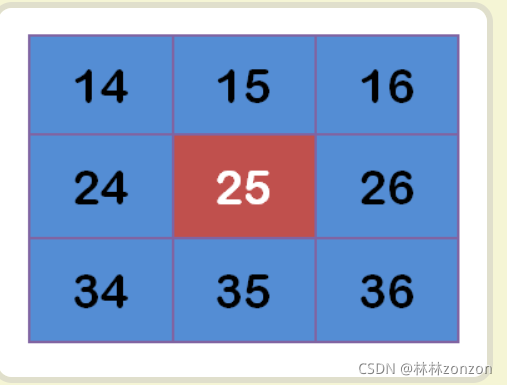
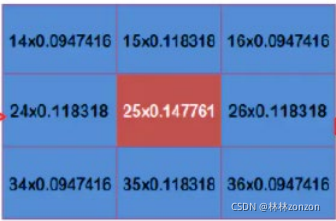
需要注意的是此函数仅能处理彩色图片,因为只有彩色图片拥有img.shape[2]元素,灰度图片没有img.shape[2]元素不能用这个方法处理。
# 高斯滤波实现,img:输入图像 kermel:输入高斯核函数
def myfilter(img,kernel):
# 读取img行数核列数
h = img.shape[0]
w = img.shape[1]
# 直接拷贝父对象
img1 = copy.copy(img)
# 去掉边缘
for i in range(1,h-1):
for j in range(1,w-1):
# 三通道处理
for c in range(0,2):
sum = 0
# 加权
for k in range(-1,2):
for l in range(-1,2):
sum += img[i+k,j+l,c]*kernel[k+1,l+1]
img1[i,j,c] = sum
return img1
同时在处理高斯滤波的时候,函数采取的是针对3*3的kernel_size进行编写的,要更改kernel_size的大小,需要更改此处的range范围。

下面是灰度图像的处理方式:
def myfilter2(img,kernel):
# 读取img行数核列数
h = img.shape[0]
w = img.shape[1]
# 直接拷贝父对象
img1 = copy.copy(img)
# 去掉边缘
for i in range(1,h-1):
for j in range(1,w-1):
sum = 0
for k in range(-1,2):
for l in range(-1,2):
sum += img[i+k,j+l]*kernel[k+1,l+1]
img1[i,j] = sum
return img1
最后整个运行代码:
import copy
import cv2
import numpy as np
#图像读取
img_y = cv2.imread('p2.jpg')
# 选择高斯生成函数3*3,其中sigama = 3
kernel = gauss(3,3)
# 打印这个生成函数
print(kernel)
# 高斯滤波处理
img1 = myfilter(img_y, kernel)
cv2.imshow('P1_yuantu',img_y)
cv2.imshow('P1_gaussian', img1)
cv2.waitKey(0)
输入输出图像结果展示:
原图与高斯滤波后
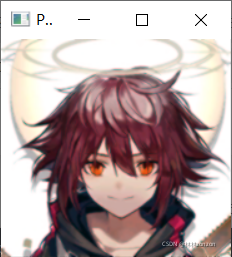
需要注意的是采取的方法很原始,如果输入的图像过大,运行时间会很久。
这方面东西挺有意思的,只是初略的学习,写些基础的东西,应该还有错漏的地方,希望有大佬们多多指点。
到此这篇关于Python+OpenCV 实现简单的高斯滤波的文章就介绍到这了,更多相关Python OpenCV 高斯滤波内容请搜索软件开发网以前的文章或继续浏览下面的相关文章希望大家以后多多支持软件开发网!