感知机模型

感知机是线性分类的二分类模型，输入为实例的特征向量，输出为实例的类别，分别用1和-1表示。感知机将输入空间（特征空间）中的实例划分为正负两类分离的超平面，旨在求出将训练集进行线性划分的超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得最优解。感知机是神经网络和支持向量机的基础。

感知机的函数公式为：f(x)=sign(w⋅x+b)f(x)=sign(w·x+b)f(x)=sign(w⋅x+b)
其中www和bbb为感知机模型参数，w∈Rnw\in R^nw∈Rn叫做权值或者权值向量，b∈Rb\in Rb∈R叫做偏差，w⋅xw·xw⋅x叫做www和xxx的内积，signsignsign是符号函数，即：sign(x)={1,x⩾0−1,x<0sign(x)=\begin{cases}1&,x\geqslant0\\-1&,x<0\end{cases}sign(x)={1−1​,x⩾0,x<0​
感知机的假设空间是定义在特征空间中所有线性分类模型的函数集合，即{f∣f(x)=w⋅x+b}\{f|f(x)=w·x+b\}{f∣f(x)=w⋅x+b}
感知机的几何解释：线性方程w⋅x+b=0w·x+b=0w⋅x+b=0对应特征空间RnR^nRn中的一个超平面SSS，其中www是超平面的法向量，bbb是超平面的截距。该超平面将特征空间分为两个部分，将特征向量分为正负两类。因此，超平面SSS成为分离超平面。

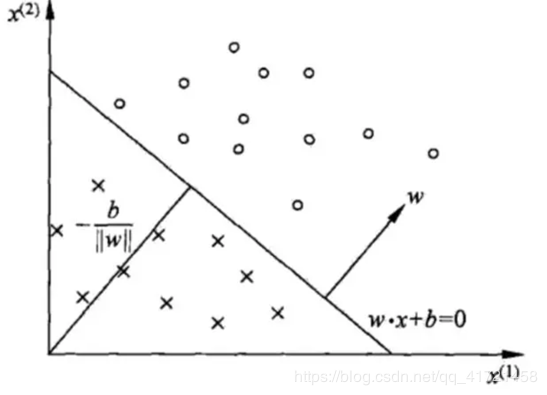
假设训练数据集是线性可分的，感知机的学习目标就是找到能够将正负实例点完全分开的超平面，即确定感知机模型参数www和bbb，因此就是确定（经验）损失函数并求损失函数的最优解，即最小化。
感知机sign(w⋅x+b)sign(w·x+b)sign(w⋅x+b)学习的损失函数定义为：
L(w,b)=−∑x∈Myi(w⋅xi+b)L(w,b)=-\sum\limits_{x\in M}y_i(w·x_i+b)L(w,b)=−x∈M∑​yi​(w⋅xi​+b)
下面给出推导：
1）首先输入空间RnR^nRn中任意点x0x_0x0​到超平面SSS的距离：1∣∣w∣∣∣w⋅x0+b∣\frac{1}{||w||}|w·x_0+b|∣∣w∣∣1​∣w⋅x0​+b∣，其中∣∣w∣∣||w||∣∣w∣∣是www的L2L2L2范数；
2）当w⋅xi+b>0w·x_i+b>0w⋅xi​+b>0时，yi=−1y_i=-1yi​=−1，而当w⋅xi+b<0w·x_i+b<0w⋅xi​+b<0时，yi=1y_i=1yi​=1。因此，对于误分类的数据(xi,yi)(x_i,y_i)(xi​,yi​)来说，−yi(w⋅xi+b)>0-y_i(w·x_i+b)>0−yi​(w⋅xi​+b)>0成立。
3）另外，误差分类点到超平面SSS的距离是1∣∣w∣∣yi(w⋅xi+b)\frac{1}{||w||}y_i(w·x_i+b)∣∣w∣∣1​yi​(w⋅xi​+b)
设MMM为超平面SSS的误分类点的集合，则所有误分类点到超平面SSS的总距离为：
1∣∣w∣∣∑x∈Myi(w⋅xi+b)\frac{1}{||w||}\sum\limits_{x\in M}y_i(w·x_i+b)∣∣w∣∣1​x∈M∑​yi​(w⋅xi​+b)
不考虑1∣∣w∣∣\frac{1}{||w||}∣∣w∣∣1​，则得到感知机的损失函数L(w,b)L(w,b)L(w,b)，即公式L(w,b)=−∑x∈Myi(w⋅xi+b)L(w,b)=-\sum\limits_{x\in M}y_i(w·x_i+b)L(w,b)=−x∈M∑​yi​(w⋅xi​+b)。
显然，损失函数L(w,b)L(w,b)L(w,b)是非负的，如果所有分类都正确，则损失函数值为0。而且分类越正确，则误分类的点离超平面越近，损失函数值越小。
因此，一个特定的样本的损失函数，在误分类时是参数w,bw,bw,b的线性参数，正确分类时是0，可以得出给定训练数据集TTT，损失函数L(w,b)L(w,b)L(w,b)是w,bw,bw,b的连续可导函数。

下面我们来看感知机的学习算法，给定一个训练数据集。
T={(x1,y1),(x2,y2),...,(xN,yN)}T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}T={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}
感知机的算法是误分类驱动的，具体采用随机梯度下降法。在极小化目标函数的过程中，并不是一次使MMM中所有误分类的点梯度下降，而是每次随机一个误分类的点使其梯度下降。
具体步骤为：
1）假设误分类点的集合为MMM，那么损失函数L(w,b)L(w,b)L(w,b)的梯度为：
▽wL(w,b)=−∑x∈Myixi\bigtriangledown_wL(w,b)=-\sum\limits_{x\in M}y_ix_i▽w​L(w,b)=−x∈M∑​yi​xi​
▽bL(w,b)=−∑x∈Myi\bigtriangledown_bL(w,b)=-\sum\limits_{x\in M}y_i▽b​L(w,b)=−x∈M∑​yi​
2）随机选取一个误分类的点(xi,yi)(x_i,y_i)(xi​,yi​)，对w,bw,bw,b更新：
w←w+ηyixiw\leftarrow w+\eta y_ix_iw←w+ηyi​xi​
b←b+ηyib\leftarrow b+\eta y_ib←b+ηyi​
式中η(0<η⩽1)\eta(0<\eta \leqslant 1)η(0<η⩽1)是步长，又称为学习率（learning rate），这样，通过迭代可以使损失函数不断减小，直到为0。
当训练数据集线性可分的时候，感知机学习算法是收敛的，并且存在无穷多个解，解会由于不同的初值或不同的迭代顺序不用而有所不同。

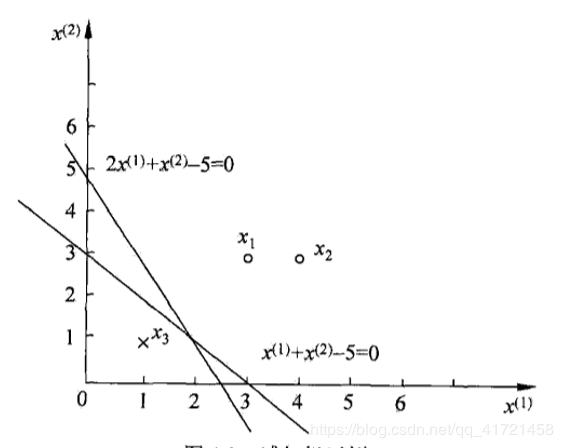
如下图所示的训练数据集，其正实例点是x1=(3,3)Tx_1=(3,3)^Tx1​=(3,3)T，x2=(4,3)Tx_2=(4,3)^Tx2​=(4,3)T，负实例点是x3=(1,1)Tx_3=(1,1)^Tx3​=(1,1)T，试用感知机学习算法的原始形式求感知机模型f(x)=sign(w⋅x+b)f(x)=sign(w·x+b)f(x)=sign(w⋅x+b)，这里，w=(w(1),w(2))Tw=(w^{(1)},w^{(2)})^Tw=(w(1),w(2))T，x=(x(1),x(2))Tx=(x^{(1)},x^{(2)})^Tx=(x(1),x(2))T。

解：构建最优化问题：
minw,bL(w,b)=−∑xi∈Myi(w⋅x+b)\mathop{min}\limits_{w,b}L(w,b)=-\sum\limits_{x_i\in M}y_i(w·x+b)w,bmin​L(w,b)=−xi​∈M∑​yi​(w⋅x+b)
按照感知机算法求解w,bw,bw,b。η=1\eta =1η=1。
1）去初值w0=0w_0=0w0​=0，b0=0b_0=0b0​=0；
2）对x1=(3,3)Tx_1=(3,3)^Tx1​=(3,3)T，y1(w0⋅x1+b0)=0y_1(w_0·x_1+b_0)=0y1​(w0​⋅x1​+b0​)=0，未能被正确分类，更新w,bw,bw,b：
w1=w0+y1x1=(3,3)T，b1=b0+y1=1w_1=w_0+y_1x_1=(3,3)^T，b_1=b_0+y_1=1w1​=w0​+y1​x1​=(3,3)T，b1​=b0​+y1​=1
得到线性模型：
w1⋅x+b1=3x(1)+3x(2)+1w_1·x+b_1=3x^{(1)}+3x^{(2)}+1w1​⋅x+b1​=3x(1)+3x(2)+1
3）对x1,x2x_1,x_2x1​,x2​，显然，yi(w1⋅xi+b1)>0y_i(w_1·x_i+b_1)>0yi​(w1​⋅xi​+b1​)>0，被正确分类，不修改w,bw,bw,b；
对x3=(1,1)Tx_3=(1,1)^Tx3​=(1,1)T，y3(w1⋅x3+b1)<0y_3(w_1·x_3+b_1)<0y3​(w1​⋅x3​+b1​)<0，被误分类，更新w,bw,bw,b：
w2=w1+y3x3=(2,2)T，b2=b1+y3=0w_2=w_1+y_3x_3=(2,2)^T，b_2=b_1+y_3=0w2​=w1​+y3​x3​=(2,2)T，b2​=b1​+y3​=0
得到线性模型：
w2⋅x+b2=2x(1)+2x(2)w_2·x+b_2=2x^{(1)}+2x^{(2)}w2​⋅x+b2​=2x(1)+2x(2)
如此继续下去，直到：
w7=(1,1)T，b7=−3w_7=(1,1)^T，b_7=-3w7​=(1,1)T，b7​=−3
w7⋅x+b7=x(1)+x(2)−3w_7·x+b_7=x^{(1)}+x^{(2)}-3w7​⋅x+b7​=x(1)+x(2)−3
对所有数据点yi(w7⋅xi+b7)>0y_i(w_7·x_i+b_7)>0yi​(w7​⋅xi​+b7​)>0，没有误分类点，损失函数达到极小。
分离超平面为：x(1)+x(2)−3=0x^{(1)}+x^{(2)}-3=0x(1)+x(2)−3=0
感知机模型为：f(x)=sign(x(1)+x(2)−3)f(x)=sign(x^{(1)}+x^{(2)}-3)f(x)=sign(x(1)+x(2)−3)
迭代过程如下表所示：

这是在计算中误分类点先取x1,x3,x3,x3,x1,x3,x3x_1,x_3,x_3,x_3,x_1,x_3,x_3x1​,x3​,x3​,x3​,x1​,x3​,x3​得到的分离超平面和感知机模型，如果在计算中误分类点依次取x1,x3,x3,x3,x2,x3,x3,x3,x1,x3,x3x_1,x_3,x_3,x_3,x_2,x_3,x_3,x_3,x_1,x_3,x_3x1​,x3​,x3​,x3​,x2​,x3​,x3​,x3​,x1​,x3​,x3​，那么得到的分离超平面是2x(1)+x(2)−5=02x^{(1)}+x^{(2)}-5=02x(1)+x(2)−5=0。
可见，感知机学习算法由于采用不同的初值或选取不同的误分类点，解可以不同。

感知机 模型