数学知识——概率统计(11):变量之间的关系描述
之前提到过描述单个随机变量的一些工具,比如正针对整体总体细节的“分布”、针对总体概述的各种统计量(期望、方差等),也提到过针多元随机变量的描述量:协方差和相关系数,现在此总结下多个变量之间关系的研究。 散点图
研究两个变量之间关系的最简单方法是散点图(scatter plot)。但好的散点图的绘制并不简单。
注:可以将数据进行抖动(jittering),即加入随机噪音弥补四舍五入的效果,以减少丢失信息对散点图的影响。
但是,抖动数据通常只应用于视觉效果,你应该避免在分析时使用经过抖动处理的数据。
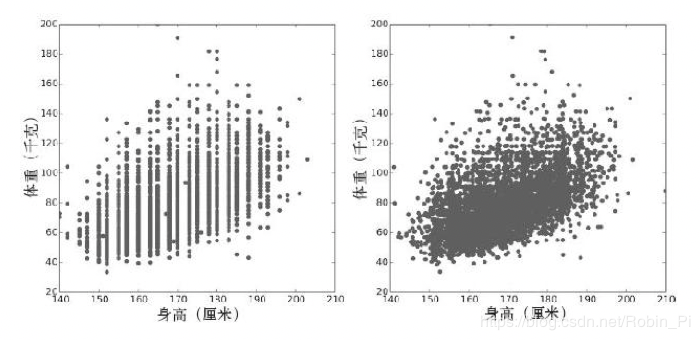
即便经过了抖动处理,散点图也不是展示数据的最佳方法。图中有很多重叠的点,遮盖了密集部分的数据,使离群值显得特别突出。这种效果称为饱和(saturation)。
散点图能让我们对变量关系有个大体了解,而其他可视化方法则可以让我们更深入地了解变量关系的本质。一种方法是对一个变量进行分区,绘制另一个变量的百分位数。
相关性相关性(correlation)是一个统计量,用于量化两个变量之间关系的强弱。
度量相关性的困难之处在于,我们需要比较的变量通常使用不同的单位。即便变量使用相同的单位,也可能来自不同的分布。
这些问题有两个常见的解决方法。
将每个值都转换为标准分数(standard score),即其偏离均值的标准差数。这种转换会产生“Pearson乘积矩相关系数”。 将每个值都转换为秩,即其在所有值的排序列表中的索引。这种转换会产生“Spearman秩相关系数”。 协方差协方差(covariance)可以度量两个变量共同变化的趋势。
Pearson相关性协方差在一些计算中非常有用,但其含义很难解释,因此人们很少将协方差作为摘要统计量。别的不提,协方差的单位是 X 和 Y 的单位乘积,这一点就很难理解。例如,BRFSS数据集中体重和身高的协方差是113千克-厘米,天晓得这是什么意思。
解决这个问题的方法之一是将偏差除以标准差,得到标准分数,然后计算标准分数的乘积。
Pearson相关性容易计算,也易于解释。因为标准分数是无量纲(无单位),所以 ρ 也是无单位的。
如果Pearson相关性接近0,你可能会认为变量之间没有关系,但这个结论并不成立。Pearson相关性只度量了线性(linear)关系。如果变量之间存在非线性关系,那么 ρ 对变量相关性强弱的估计就可能是错误的。
Spearman秩相关如果变量之间的关系是线性的,而且变量大致符合正态分布,那么Pearson相关性能够很好地说明相关性的强弱。但是离群值会影响Pearson相关性的稳健性。Spearman秩相关能够缓解离群值以及偏斜分布的的影响,也可以用于描述变量的相关性。要计算Spearman相关性,必须计算每个值的秩(rank),即该值在排序样本中的索引。
相关性和因果关系记住:“相关性并不意味着因果关系”
参考:
概率思维
作者:Robin_Pi