Python:三维空间的概率密度函数
大家肯定都有听说过正态分布,其实正态分布只是概率密度分布的一种,正态分布的概率密度函数均值为μ ,标准差σ是高斯函数的一个实例:
f(x;μ,σ)=1σ2πexp(−(x−μ)22σ2)
f(x ; \mu, \sigma)=\frac{1}{\sigma \sqrt{2 \pi}} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)
f(x;μ,σ)=σ2π1exp(−2σ2(x−μ)2)
在一维上只有x一个变量,μ 均值,σ标准差。
正态分布具有两个参数μ和σ的连续型随机变量的分布,第一
参数μ是服从正态分布的随机变量的均值,第二个参数σ^2是此随机变量的方差,所以正态分布记作N(μ,σ2)。
实际工作中,正态曲线下横轴上一定区间的面积反映该区间的例数占总例数的百分比,或变量值落在该区间的概率。
因此一维的概率密度分布即正态分布,很好的表示数据在哪个区间集中,使我们对整体数据有一个大概的把握。
本文的重点在于二维概率密度函数:
f(x,y)=(2πσ1σ21−ρ2)−1exp[−12(1−ρ2)((x−μ1)2σ12−2ρ(x−μ1)(y−μ2)σ1σ2+(y−μ2)2σ22)]
f(x, y)=\left(2 \pi \sigma_{1} \sigma_{2} \sqrt{1-\rho^{2}}\right)^{-1} \exp \left[-\frac{1}{2\left(1-\rho^{2}\right)}\left(\frac{\left(x-\mu_{1}\right)^{2}}{\sigma_{1}^{2}}-\frac{2 \rho\left(x-\mu_{1}\right)\left(y-\mu_{2}\right)}{\sigma_{1} \sigma_{2}}+\frac{\left(y-\mu_{2}\right)^{2}}{\sigma_{2}^{2}}\right)\right]
f(x,y)=(2πσ1σ21−ρ2)−1exp[−2(1−ρ2)1(σ12(x−μ1)2−σ1σ22ρ(x−μ1)(y−μ2)+σ22(y−μ2)2)]
因为生活中的很多数据都是高维度的,从简单的二维说起。二维上的数据生活中有很多:身高和体重,血压和血脂等等。如果能够像一维正态分布那样做出图像来看,就十分直观,而本文就是介绍如何作二维概率密度函数的图像。
首先贴上数据集:
链接:https://pan.baidu.com/s/1RJCwi4-8_hByY6-rCepJgQ
提取码:88ew
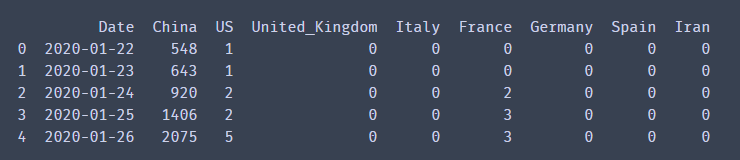
数据是截至4.25日的重点国家新冠肺炎感染人数,有中国、美国、法国、意大利等。
本文采取的是中国和意大利进行对比分析。
import numpy as np
import matplotlib.pyplot as plt
import math
import mpl_toolkits.mplot3d
import math
import pandas as pd
data = pd.read_csv('D:/桌面/1.csv')
print(data.head())
x = data.iloc[:,1]
y = data.iloc[:,7]
x = x.values
y = y.values
首先根据公式我们先把2个维度的均值和方差分别计算出来,以及公式中需要的相关系数。
u1 = x.mean()
u2 = y.mean()
o1 = x.std()
o2 = y.std()
from scipy.stats import pearsonr
p = pearsonr(x, y)[0]
print(u1, u2, o1, o2, p)
# 输出:(r, p)
# r:相关系数[-1,1]之间
# p:相关系数显著性
相关系数也就是皮尔逊系数,把2个维度数据给入后,会输出相关系数和相关系数显著性。
相关系数取值范围是(-1,1),越接近1则说明越相关。不过我们也不能说中国感染人数和西班牙感染人数相关,这里更确切地解释应该是感染人数的趋势比较。
X, Y = np.meshgrid(x, y)
z = (1/(2*math.pi*o1*o2*pow(1-pow(p,2),0.5)))*np.exp(-1/(2*(1-p*p))*(((X-u1)*(X-u1))/(o1*o1)-2*p*(X-u1)*(Y-u2)/(o1*o2)+(Y-u2)*(Y-u2)/(o2*o2)))
这里X,Y是对原始数据进行网格化,其实就相当于最后成果图的横纵坐标,只是转换一下得以输入作图。
z就是上文的二维密度函数用python来表达了。比较麻烦,注意里面有上面算出的2个维度的均值,方差和皮尔逊系数。
plt.rcParams['font.sans-serif'] = ['KaiTi'] # 用来正常显示中文字符
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(10,10), dpi=300)
ax = plt.subplot(111, projection='3d')
ax.plot_surface(X, Y, z,
cmap='rainbow', alpha=0.9)
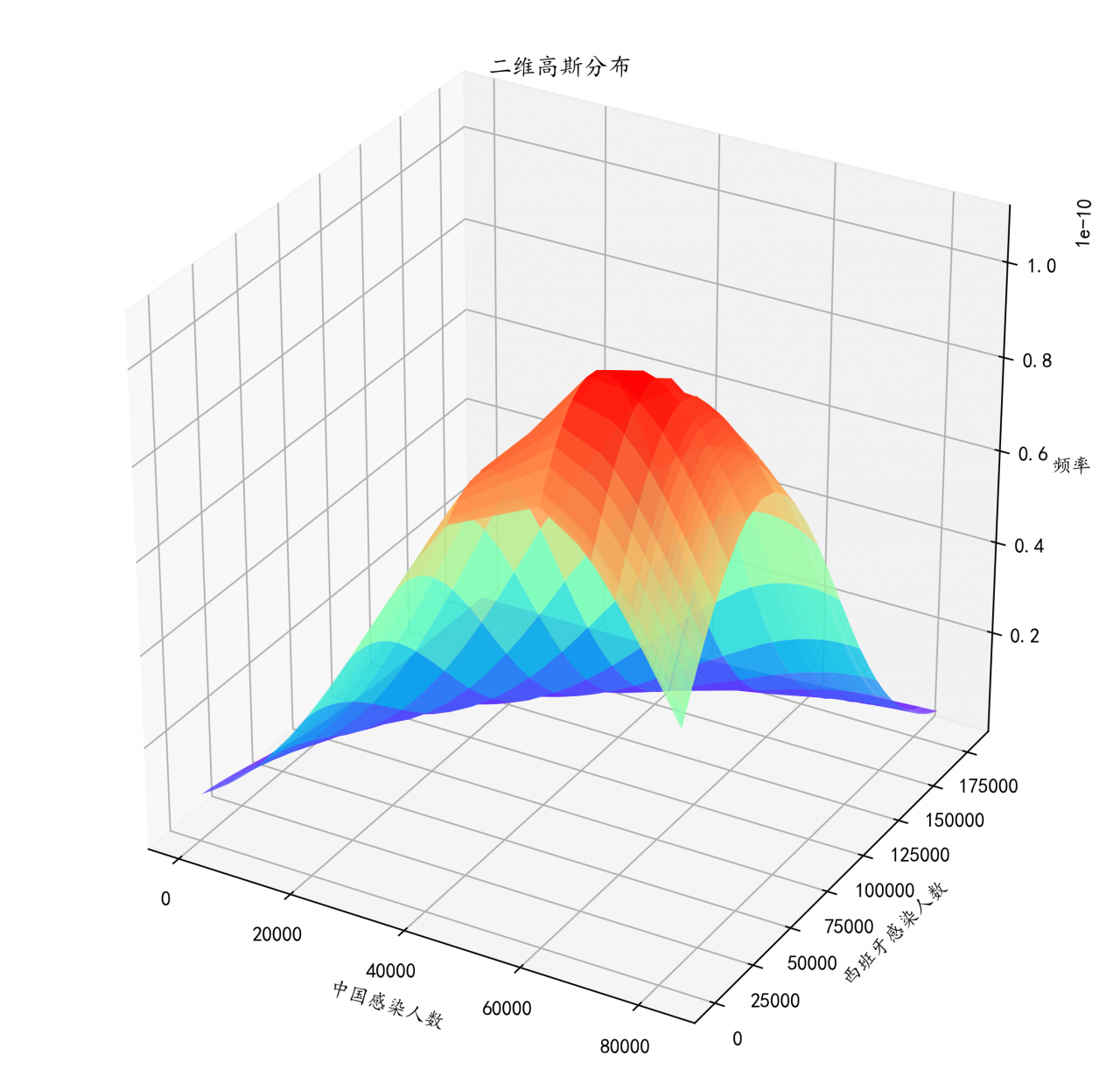
ax.set_xlabel('中国感染人数')
ax.set_ylabel('西班牙感染人数')
ax.set_zlabel('频率')
ax.set_title("二维高斯分布")
plt.savefig('D:/桌面/1.png', bbox_inches='tight', pad_inches=0.0)
这就是很基础的一些画图设置了,相似的就不再赘述,重点 谈谈plot_surface。
plot_surface中的X,Y,z其实上文以及解释过了,就是相应的坐标和函数,那么cmap是什么呢,camp是颜色盘,值定位rainbow就是彩虹色,从下图就可以看出,数据越集中的地方,颜色就越深。这里还有一个颜色盘是coolwarm,不过个人感觉没rainbow好看,不妨小伙伴们试一试。
 原创文章 5获赞 8访问量 730
关注
私信
展开阅读全文
原创文章 5获赞 8访问量 730
关注
私信
展开阅读全文
作者:ABin_203