[Python]利用python实现复杂网络的博弈（1）——Networkx相关知识

Networkx入门

首先，我们先使用Constructor来构建一个新的图：

import networkx as nx G = nx.Graph()

这个图里面并没有点，也没有边，我们可以采用如下的方式来添加点和边：

G.add_node(0) G.add_nodes_from([1, 2, 3, 4, 5, 6, 7, 8]) G.add_edge(0,1) G.add_edges_from([(0,3), (1,4), (1,2), (2,5), (3,6), (3,4), (4,7), (4,5), (5,8), (6,7), (7,8)])

在networkx里面，node可以是除了None之外的任意hashable类型，比如char,string甚至于function，xml等也可以成为node，当然在这里我们仅仅演示一下最为常见的int。

对于点和边的添加，其实还有其他方式，比如

G.add_star([1, 2, 3])# equal to G.add_edges_from([(1,2), (1,3)]) G.add_path([1, 2, 3])# equal to G.add_edges_from([(1,2), (2,3)]) G.add_circle([1, 2, 3])# equal to G.add_edges_from([(1,2), (2,3), (3,1)])

点和边的移除，只需要将API中的add改为remove即可:

G.remove_node(0) G.remove_nodes_from([1, 2]) G.remove_edge(0,1) G.remove_edges_from([(0,3), (1,4)])

如果希望一口气移除全部，请使用G.clear()

Networkx的基本数据结构，节点和边的属性

我们可以查看一下G的具体结构：

>>>print(G[0]) {1: {}, 3: {}} >>>print(list(G[0])) [1, 3] >>>print(G[0][1]) {} >>>print(G.node) [0, 1, 2, 3, 4, 5, 6, 7, 8] >>>print(G.node[0]) {}

我们可以发现，G[0]这个操作，会为我们返回一个词典，他的key值即为他的邻居，而value值为一个空的字典，这个字典，正是这个边的属性值。Networkx的这种结构被称作"the dictionary of dictionaries of dictionaries"，因而，我们也可以得知G的迭代操作：

>>>print([n for n in G]) [0, 1, 2, 3, 4, 5, 6, 7, 8] >>>print([nbr for nbr in G[0]]) [1, 3]

我们可也可以通过G[0][1]来访问这条边所具有的属性。如果我们希望访问点的属性，则需要使用node方法，下面是关于属性的展示：

>>>G[0]['type'] = 'A' #you should use 'node' to access the attribute of nodes! TypeError: 'AtlasView' object does not support item assignment >>>G.node[0]['type'] = 'A' >>>print(G.node[0]) {'type': 'A'} >>>G[0][1]['weight'] = 0.1 >>>print(G[0]) {1: {'weight': 0.1}, 3: {}}

虽然修改节点属性需要额外调用node成员，但是判断点的存在性和统计点的个数时，可以直接使用G:

>>>10 in G False >>>len(G) 10

同时，图也是具有属性的，与点类似，不能通过G['attr']直接访问，而必须通过graph成员

>>>G.graph['use'] = 'gaming' >>>print(G.graph) {'use': 'gaming'}

同时，直接在创建中添加属性也是可行的：

G = nx.Graph(use = 'gaming') G.add_node(0, type = 'A') G.add_edge(1,2,weight = 1)

边具有一个特殊的属性weight，也就是权重，networkx具有一个特殊的API来提供批量创建带权重的边：

e=[('a','b',0.3),('b','c',0.9),('a','c',0.5),('c','d',1.2)] G.add_weighted_edges_from(e)

对于其他没有特殊API的属性，则会麻烦一些：

G.add_edges_from([(1,2,{'color':'blue'}), (2,3,{'color':'red'})]) G.add_edges_from([(1,2), (3,4)], color = 'red')

另外，区分一下node和nodes，前者是成员，后者是方法，(但是请注意，对于边来说，只有edges而没有edge)

>>>print(G.node) [0, 1, 2, 3, 4, 5, 6, 7, 8] >>>print(G.nodes()) [0, 1, 2, 3, 4, 5, 6, 7, 8] >>>print(G.nodes(data = True)) [(0, {'type': 'A'}), (1, {}), (2, {}), (3, {}), (4, {}), (5, {}), (6, {}), (7, {}), (8, {})] >>>print(G.nodes(data = 'type')) [(0, 'A'), (1, None), (2, None), (3, None), (4, None), (5, None), (6, None), (7, None), (8, None)]

假设我们的点具有一个名为color的属性，我们就可以采取下面这种方式将color提取出来：

node_color = list(zip(*G.nodes(data = 'color')))[1]

属性的移除和字典一样，采用del命令，此处不再赘述。

networkx中的图论相关API 获取一个图的总结点/边数 获取总结点数： num = G.number_of_nodes() num = G.order() num = len(G) 获取边数： num = G.number_of_edges() num = G.size() 判断邻接信息 关于邻接的几个迭代器

运行：

for n, nbrs in G.adjacency(): print(n, nbrs)

或者

for n in G: print(n, G.adj[n]) # same as print(n, G[n])

可得：

0 {1: {'weight': 0.1}, 3: {}} 1 {0: {'weight': 0.1}, 4: {}, 2: {}} 2 {1: {}, 5: {}} 3 {0: {}, 6: {}, 4: {}} 4 {1: {}, 3: {}, 7: {}, 5: {}} 5 {2: {}, 4: {}, 8: {}} 6 {3: {}, 7: {}} 7 {4: {}, 6: {}, 8: {}} 8 {5: {}, 7: {}}

而G.neighbors(n)与上面不同，其返回的是一个dict的iter

获取邻接矩阵 >>>nx.adj_matrix(G) (0, 1) 0.1 (0, 3) 1.0 (1, 0) 0.1 (1, 2) 1.0 (1, 4) 1.0 (2, 1) 1.0 (2, 5) 1.0 (3, 0) 1.0 (3, 4) 1.0 (3, 6) 1.0 (4, 1) 1.0 (4, 3) 1.0 (4, 5) 1.0 (4, 7) 1.0 (5, 2) 1.0 (5, 4) 1.0 (5, 8) 1.0 (6, 3) 1.0 (6, 7) 1.0 (7, 4) 1.0 (7, 6) 1.0 (7, 8) 1.0 (8, 5) 1.0 (8, 7) 1.0 判断一个点的节点度

G下面有一个方法degree，也有一个成员degree，二者在大部分某些操作上是相同的：

>>>G.degree[0]#same as G.degree()[0] 2 >>>list(G.degree)#same as list(G.degree()) [(0, 2), (1, 3), (2, 2), (3, 3), (4, 4), (5, 3), (6, 2), (7, 3), (8, 2)]

但是方法是可以含参的

>>>G.degree(0) 2 >>>G.degree([0,1,2]) [(0, 2), (1, 3), (2, 2)] 判断两点是否相连

等价于判断边的存在性，可以采用：

>>> (1,2) in G.edges() True >>> G.has_edge(1,2) True >>> 2 in G.neighbors(1) True

另外，如果不试图判断两点是否直接相连，而是存在的path的话，应当使用nx.has_path(G, source, target)

利用matplotlib.pyplot对networkx的网络进行绘图

networkx本身不是一个绘图工具，但是他也提供draw这个方法。下面是这个方法的官方说明：

draw(G,pos=None, ax=None,hold=None, **kwds)

G: 需要画出来的图像

pos：图像中各个点的坐标，应当是一个二维tuple的list，且长度大于G中的节点个数

ax和hold：与pyplot相关的参数

**kwd：可选的keyword如下(参考)：

nodelist(list, default: G.node) ：需要画出的点 edgelist(list, default: G.edge)：需要画出的边 node_size(scalar or array, default: 300)：控制点的大小，如果使用一个数组存储不同的值，可以做到另不同的点大小不同，但是此数组的长度必须与nodelist的长度相同 node_color(color string or array of floats, default: 'r')：控制点的颜色，可以通过string或者float的数组，如果是数值，将自动映射到cmap上，cmap见后。可以查询matplotlib.scatter来获知更多 node_shape(string, default: 'o')通过一系列的字符来控制点的形状，可在’so^>v<dph8’里面选择 alpha(float, default: 1.0) 控制图像的不透明度 cmap(Matplotlib colormap, default:None)：图像的色图，用来映射某些值 vmin, vmax(float, default:None)：色图的最大值与最小值 linewidth([None|scalar|sequence])：符号边框的线宽（默认是1.0) width(float, default: 1.0)线宽 edge_color, edge_cmap, edge_vmin, edge_vmax：见上 style(string, default: solid)：线的格式，可在solid|dashed|dotted,dashdot里面选择 labels(dictionary,default:None)：节点的标签，key为节点，value为节点的标签值 label(string)：图例的标签 font_size(int, default:12)：字体大小 font_color(string, default:'black')：字体颜色 font_weight(string, default: 'normal')：字体粗细 font_family(string, default:'sans-serif')：字体

当然，各位不要害怕，我们不会一上来就讲解过于复杂的东西，我们先讲了一下基础的东西：

画一个最简单的图吧！

最简单的情况下，我们只需要使用:

import matplotlib.pyplot as plt nx.draw(G) plt.show()

便可以画出一幅图，如图：

如何确定画面上各个点的位置？

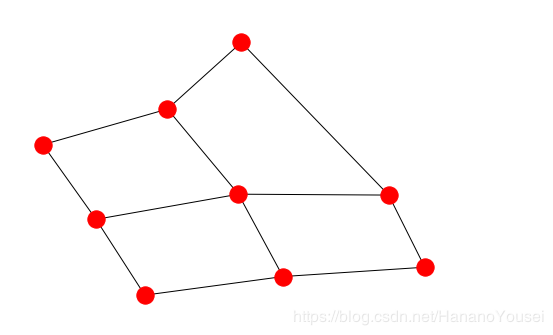
这里就需要用到我们的pos参数了。首先我们尝试自己创建：

pos = [(1,3), (2,3), (3,3), (1,2), (2,2), (3,2), (1,1), (2,1), (3,1)] nx.draw(G, pos) plt.show()

得到的结果如图：

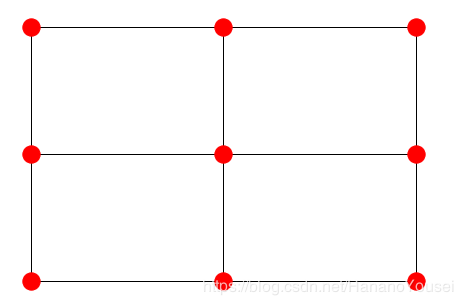
但是实践里面，我们不可能给一个具有大量节点的图挨个赋值，这个时候可以使用nx自带的生成pos的函数:

pos = nx.bipartite_layout(G, [0, 1, 2])

结果是：

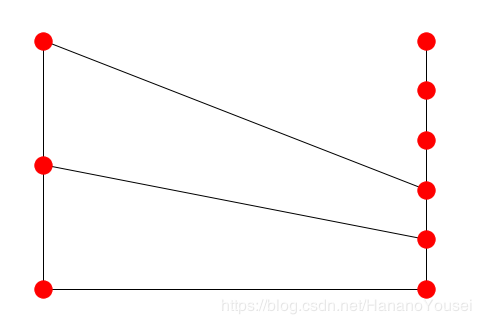
pos = nx.circular_layout(G)# or use `nx.draw_circular(G)` directly

结果是：

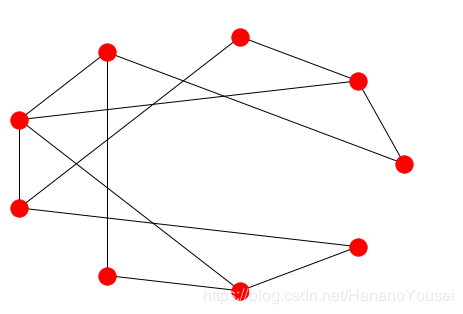
pos = nx.kamada_kawai_layout(G)# or use `nx.draw_kamada_kawai(G)` directly

结果是：

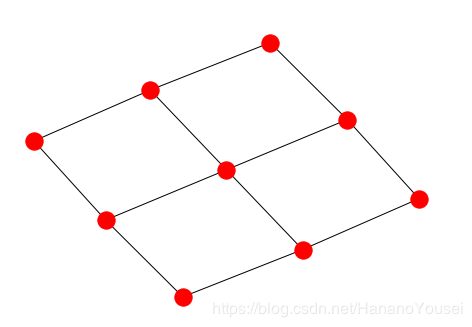
pos = nx.spring_layout(G)# or use `nx.draw_spring(G)` directly

结果是：

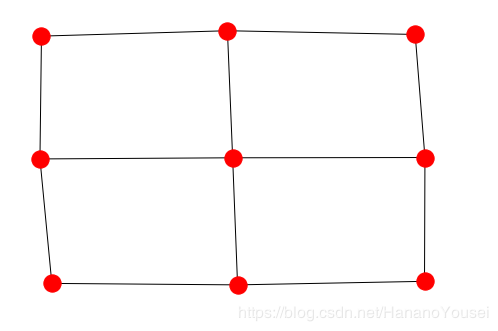
pos = nx.spectral_layout(G)# or use `nx.draw_spectral(G)` directly

结果是：

如何让图显得更花里胡哨呢？

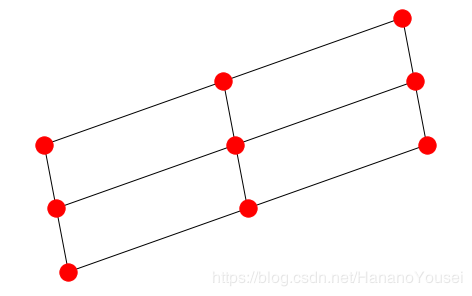
没必要一个个演示，一起上吧：

nx.draw(G, pos, labels = labels, node_size = 1000,node_shape = '8', font_size = 20, node_color = 'black', font_color = 'white', style = 'dashed', font_weight = 'bold') plt.show()

结果是：

如何让不同的节点具有不同的颜色？

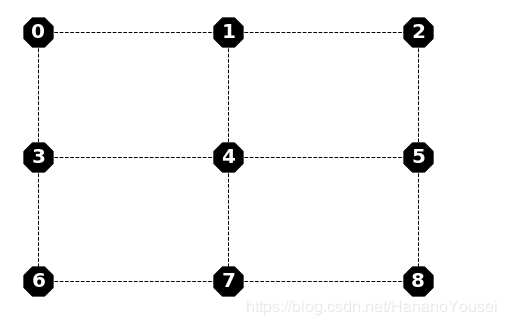
如果想要得知不同颜色的名称，请查询:【Python学习】matplotlib的颜色

colors = ['red'] * 3 + ['black'] * 3 + ['purple'] * 3 edge_colors = ['black', 'red', 'peru', 'khaki', 'yellow', 'greenyellow', 'green', 'cyan', 'slategray', 'blue', 'violet', 'crimson'] width = [1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6] nx.draw(G, pos, node_color = colors, edge_color = edge_colors, width = width) plt.show()

结果是：

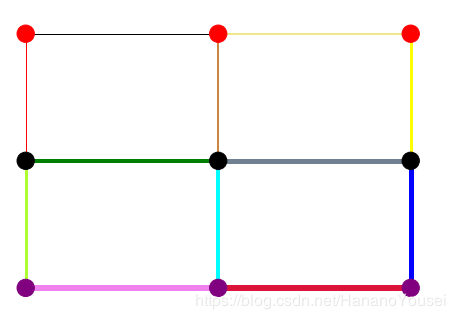
同样，你可以依据node的某些特征来构建colors的list

请务必注意，colors的长度必须和node_list一致，不然会报错，这一点和pos是不同的，pos的值多于node_list并不会导致报错

Colormap的使用

关于Colormap的使用，请查询matplotlib的官方中文文档

首先，我们给node_color附一个确定的float数组，比如说:

colors = [] for n in G: colors.append(G.degree(n))

然后，我们只要这样使用:

nx.draw(G, pos, node_color = colors, cmap = plt.cm.magma_r)

就可以得到:

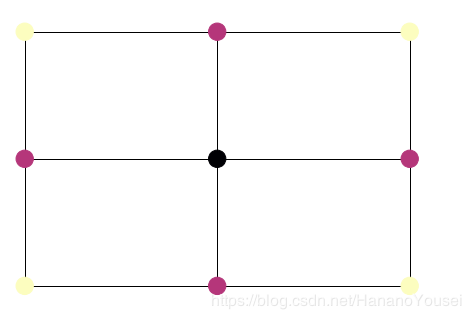
这样可以将节点的某些数值特征映射到颜色上。

作者：Span_1024

用python 博弈 复杂网络 networkx Python