分治算法

分治算法的基本思想 将原始问题划分为规模较小的子问题。 递归或迭代求解每个子问题的解。 将子问题的解综合得到原问题的解。 分治算法的步骤 分解
将要解决的问题划分成若干规模较小的同类问题。 求解
当子问题划分得足够小时，用较简单的方法解决。 合并
按原问题的要求，将子问题的解逐层合并构成原问题的解。 分治算法的特点 原问题可以划分为规模较小的子问题。 子问题与原问题具有相同的性质。 子问题之间可以彼此独立地求解。 划分时子问题的规模尽可能均衡。 子问题规模足够小时可直接求解。 子问题的解综合能得到原问题的解。 算法的分析方法：递推方程。 算法实现：递归或迭代。 分治算法时间分析

W( n ) = W( |P1| ) + W( |P2| ) +…+ W( |Pk| ) + f( n )
W( c ) = C

P1, P2, …, Pk为划分后产生的子问题
f( n )为划分子问题以及将子问题的解综合得到原问题解的总工作量
规模为c的最小子问题的工作量为C

分治算法两类常见的递推方程

分治算法的应用举例 1.二分检索、快速排序、归并排序。
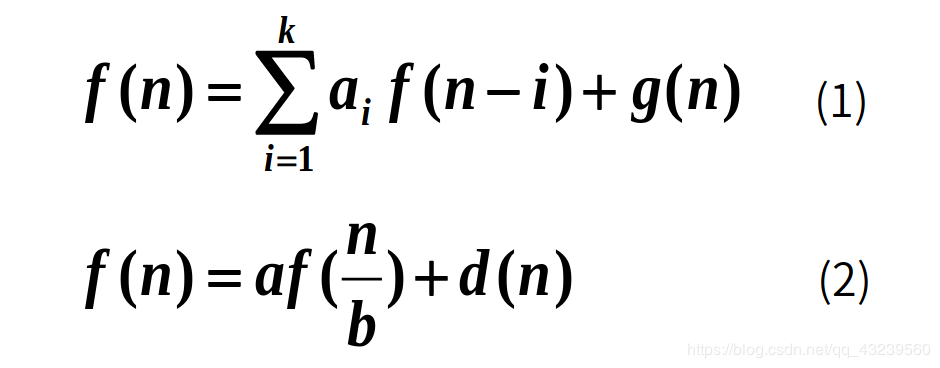
作者：Cassie~

分治算法 算法