KNN(K最近邻)分类算法_糖潮丽子的博客
我们本篇博客来学习KNN算法的原理,超参数调整,以及KNN算法应用。
kNN算法:K最近邻(kNN,k-NearestNeighbor)分类算法。

邻近算法,或者说K最近邻(kNN,k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。KNN是一种分类(classification)算法,它输入基于实例的学习(instance-based
learning),属于懒惰学习(lazy
learning)即KNN没有显式的学习过程,也就是说没有训练阶段,数据集事先已有了分类和特征值,待收到新样本后直接进行处理。与急切学习(eager
learning)相对应。
KNN是通过测量不同特征值之间的距离进行分类。
思路:如果一个样本在特征空间中的k个最邻近的样本中的大多数属于某一个类别,则该样本也划分为这个类别。KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
目标:
熟知KNN算法的基本原理 能够使用KNN算法实现分类与回归任务 能够调整算法的超参数 熟知KD树的构建与邻居选择 2、举例在讲解KNN之前,我们来看如下的数据集:
| 语文 | 数学 | 学生 |
|---|---|---|
| 95 | 93 | 好 |
| 90 | 92 | 好 |
| 91 | 96 | 好 |
| 85 | 82 | 中 |
| 83 | 87 | 中 |
| 80 | 84 | 中 |
| 61 | 69 | 差 |
| 66 | 63 | 差 |
| 72 | 65 | 差 |
| 83 | 77 | ? |
我们将以上数据映射到空间中,进行绘制。因为数据具有两个特征,因此,每条数据对应二维空间中的一个点。
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = "SimHei"
plt.rcParams["axes.unicode_minus"] = False
plt.rcParams["font.size"] = 12
good = np.array([[95, 93], [90, 92], [91, 96]]) #good 好学生
medium = np.array([[85, 82], [83, 87], [80, 84]]) #中等学生
bad = np.array([[61, 69], [66, 63], [72, 65]]) #差学生
unknown = np.array([[83, 77]]) #未知
plt.scatter(good[:, 0], good[:, 1], color="r", label="优等生")
plt.scatter(medium[:, 0], medium[:, 1], color="g", label="中等生")
plt.scatter(bad[:, 0], bad[:, 1], color="b", label="差等生")
plt.scatter(unknown[:, 0], unknown[:, 1], color="orange", label="未知")
plt.legend()
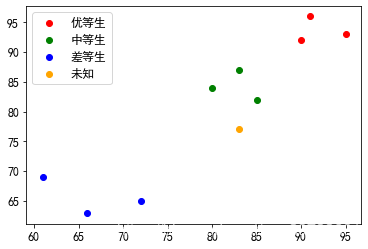
上图中橙色的点(样本),最可能的类别是( B )。
A 优等生
B 中等生
C 差等生
D 三种可能概率均等
我们要确定绿点属于哪个颜色(红色或者蓝色),要做的就是选出距离目标点距离最近的k个点,看这k个点的大多数颜色是什么颜色。当k取3的时候,我们可以看出距离最近的三个,分别是红色、红色、蓝色,因此得到目标点为红色。
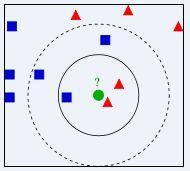
算法的描述:
1)计算测试数据与各个训练数据之间的距离;
2)按照距离的递增关系进行排序;
3)选取距离最小的K个点;
4)确定前K个点所在类别的出现频率;
5)返回前K个点中出现频率最高的类别作为测试数据的预测分类
从上例的运行结果中,我们发现,相似度较高的样本,映射到 n 维空间后,其距离会比相似度较低的样本在距离上更加接近,这正是KNN算法的核心思维。
KNN(K-Nearest Neighbor),即近邻算法。
K近邻就是K个最近的邻居,当需要预测一个未知样本的时候,就由与该样本最接近的K个邻居来决定。
KNN既可以用于分类问题,也可以用于回归问题。
当进行分类预测时,使用K个邻居中,类别数量最多(或加权最多)者,作为预测结果。
当进行回归预测时,使用K个邻居的均值(或加权均值),作为预测结果。
KNN算法的原理在于,样本映射到多维空间时,相似度较高的样本,其距离也会比较接近,反之,相似度较低的样本,其距离也会比较疏远。
超参数,是指我们在训练模型之前,需要人为指定的参数。 该参数不同于模型内部的参数,模型内部的参数是通过训练数据,在训练过程中计算得出的。超参数的不同,可能会对模型的效果产生很大影响。
5.1 K值K值的选择,会直接影响到预测结果。
当K值较小时,模型会较依赖于附近的邻居样本,具有较好敏感性,但是稳定性会较弱,容易导致过拟合。
当K值较大时,稳定性增加,但是敏感性会减弱,容易导致欠拟合。
通常情况下,我们可以通过交叉验证的方式,选择最合适的K值。
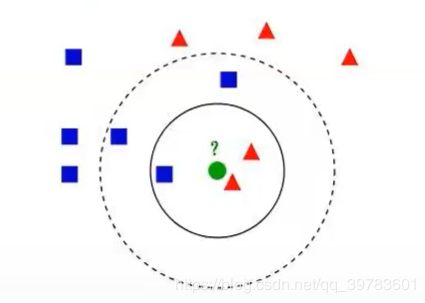
当K=3时,在实心圈内绿色的圆圈预测为红色的三角。
当K=5时,在虚线圈内绿色的圆圈预测为蓝色的方块。
K值取值的不同,会影响到预测结果的不同。
K:临近数,即在预测目标点时取几个临近的点来预测。
K值得选取非常重要,因为:
K的取法:
常用的方法是从k=1开始,使用检验集估计分类器的误差率。重复该过程,每次K增值1,允许增加一个近邻。选取产生最小误差率的K。
一般k的取值不超过20,上限是n的开方,随着数据集的增大,K的值也要增大。
在scikit-learn中,距离默认使用闵可夫斯基距离(minkowski),p 的值为2。假设n维空间中的两个点为X与Y:

可知:
当p为1时,距离就是曼哈顿距离,当p为2时,距离就是欧几里得距离(欧氏距离)。
权重可以分为两种:
统一权重:所有样本的权重相同。 距离加权权重:样本的权重与待预测样本的距离成反比。(1)分类预测时:
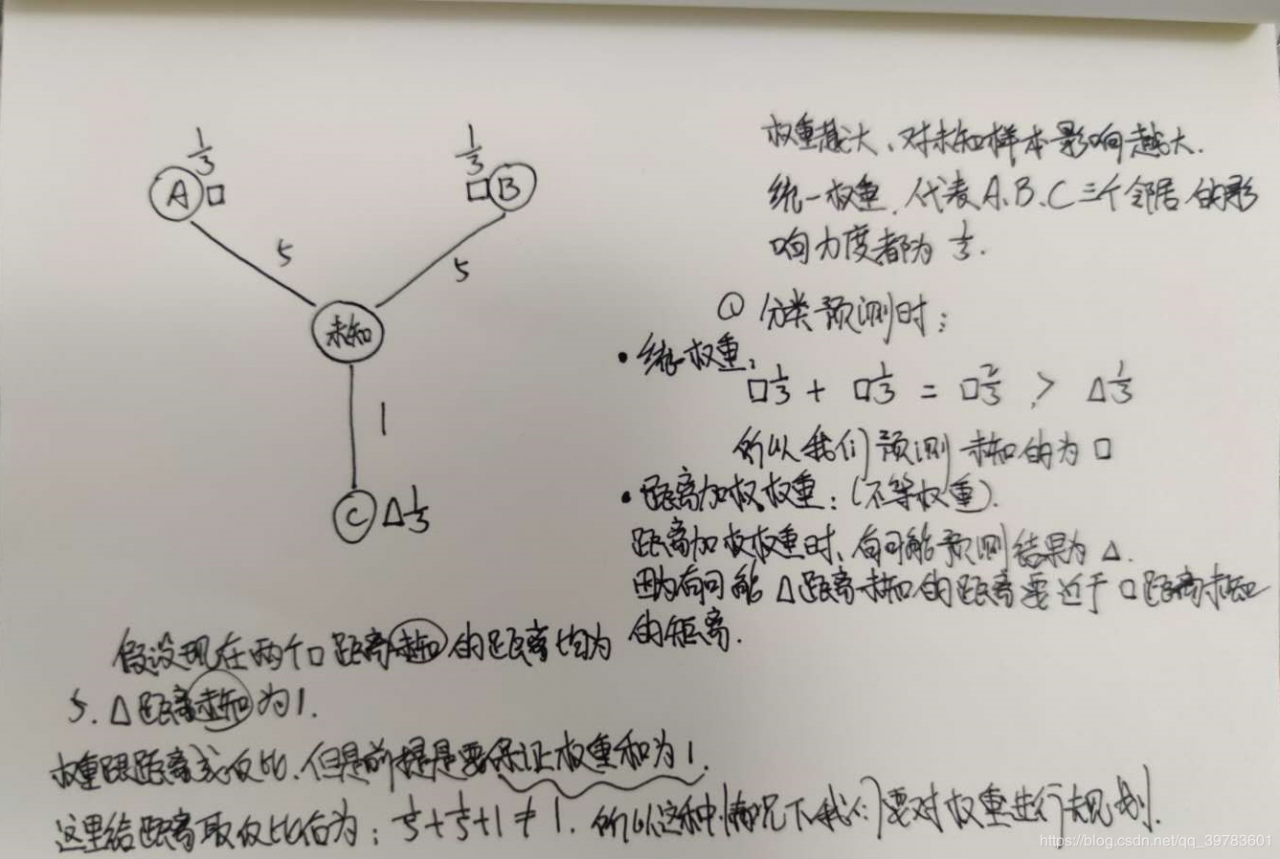

(2)回归预测时:

注意:
做个练习吧:
使用KNN预测未知样本A,假设的值为3,三个最近的邻居是B,C 与D。A距离B,C ,D【】 【】【【】】【】的【【】】【】【】【[【】【】】【【】[【】【】【】【】[【】【】【】【】】【【】【】】【【】】【】【】距【【】】【】离分别是2,3,5。如果按照距离加权的方式计算权重,则B,C ,D 的权重分别是( D)。

解题步骤:

KNN算法的执行过程如下:
确定算法超参数。 确定近邻的数量。 确定距离度量方式。 确定权重计算方式。 其他超参数。 从训练集中选择离待预测样本A最近的K个样本。 根据这K个样本预测A。 对于分类,使用个K样本的类别(或加权类别)预测A。 对于回归,使用个K样本目标值( y )的均值(或加权均值)预测A。练习:
给定待预测样本 A,如果在训练集中,存在两个(或更多)不同的邻居 N1与N2 (N1与 N2的标签不 同),二者距离 A的距离相等,假设K 的值为1,则此时选择哪个邻居较为合理? (D)
A 选择 N1
B 选择 N2
C 随机选择
D 根据 N1与 N2在训练集中出现的先后顺序选择。
E C或D
解析:
算法一定要保证确定性,所以选择D。
我们以鸢尾花数据集为例,通过KNN算法实现分类任务。同样,为了方便可视化,我们只取其中的两个特征。
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
iris = load_iris()
X = iris.data[:, :2]
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)
# n_neighbors:邻居的数量。
# weights:权重计算方式。可选值为uniform与distance。
# uniform:所有样本统一权重。
# distance:样本权重与距离成反比。
knn = KNeighborsClassifier(n_neighbors=3, weights="uniform")
knn.fit(X_train, y_train)
y_hat = knn.predict(X_test)
print(classification_report(y_test, y_hat))
代码解析: KNeighborsClassifier 实现了K最近邻居投票算法的分类器。 KNeighborsClassifier中的参数:
n_neighbors:邻居的数量。
weights:权重计算方式。可选值为uniform与distance。
uniform:所有样本统一权重。
distance:样本权重与距离成反比。
KNeighborsRegressor 回归预测。
结果:
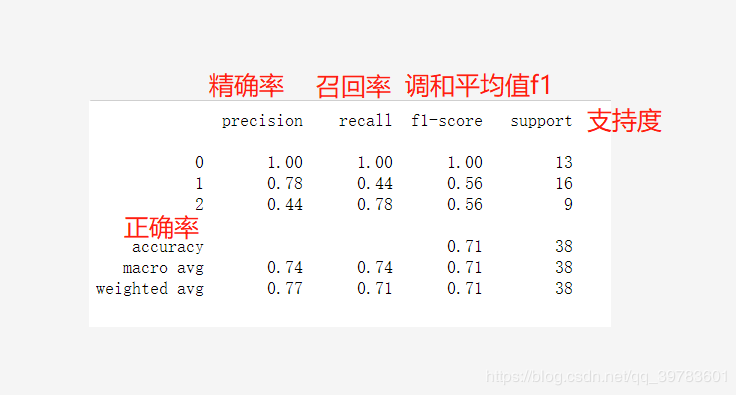
对分类模型评估不理解的可以参考这篇文章。这里!!!
7.2 超参数对模型的影响当然,不同的超参数值,会直接影响模型的分类效果。
我们可以从决策边界中发现这一点。
from matplotlib.colors import ListedColormap
def plot_decision_boundary(model, X, y):
color = ["r", "g", "b"]
marker = ["o", "v", "x"]
class_label = np.unique(y)
cmap = ListedColormap(color[: len(class_label)])
x1_min, x2_min = np.min(X, axis=0)
x1_max, x2_max = np.max(X, axis=0)
x1 = np.arange(x1_min - 1, x1_max + 1, 0.02)
x2 = np.arange(x2_min - 1, x2_max + 1, 0.02)
X1, X2 = np.meshgrid(x1, x2)
Z = model.predict(np.c_[X1.ravel(), X2.ravel()])
Z = Z.reshape(X1.shape)
plt.contourf(X1, X2, Z, cmap=cmap, alpha=0.5)
for i, class_ in enumerate(class_label):
plt.scatter(x=X[y == class_, 0], y=X[y == class_, 1],
c=cmap.colors[i], label=class_, marker=marker[i])
plt.legend()
from itertools import product
weights = ['uniform', 'distance']
ks = [2, 15]
plt.figure(figsize=(18, 10))
# 计算weights与ks的笛卡尔积组合。这样就可以使用单层循环取代嵌套循环,
# 增加代码可读性与可理解性。
for i, (w, k) in enumerate(product(weights, ks), start=1):
plt.subplot(2, 2, i)
plt.title(f"K值:{k} 权重:{w}")
knn = KNeighborsClassifier(n_neighbors=k, weights=w)
knn.fit(X, y)
plot_decision_boundary(knn, X_train, y_train)
结果:
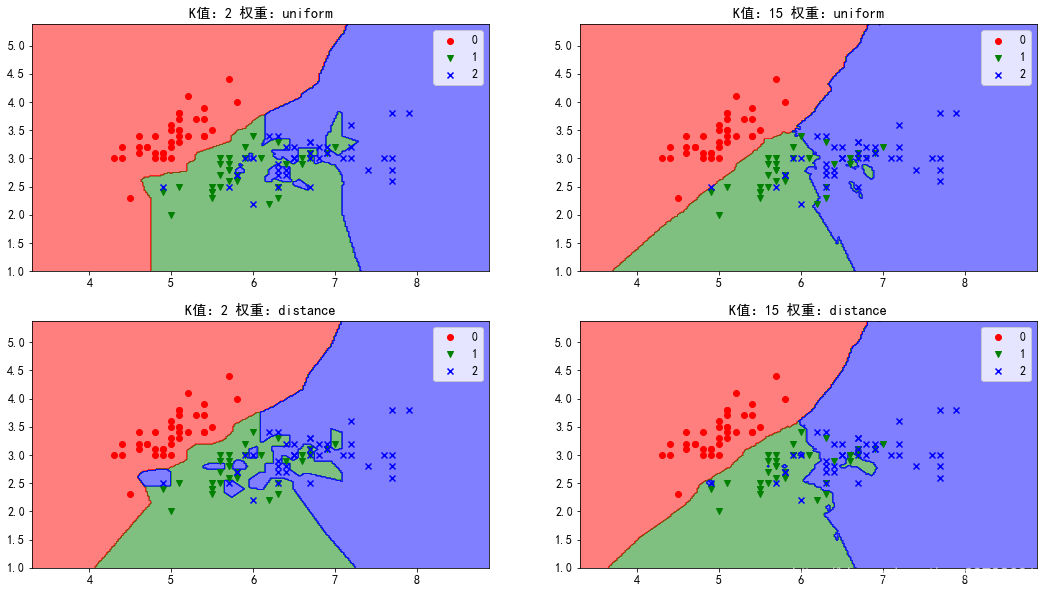
通过决策边界,我们可以得出如下结论:
在实际应用中,我们很难单凭直觉,就能够找出合适的超参数,通常,我们可以通过网格交叉验证的方式,找出效果最好的超参数。
from sklearn.model_selection import GridSearchCV #网格搜索
knn = KNeighborsClassifier()
# 定义需要尝试的超参数组合。
grid = {"n_neighbors": range(1, 11, 1), "weights": ['uniform', 'distance']} # 20种超参数
# estimator:评估器,即对哪个模型调整超参数。
# param_grid:需要检验的超参数组合。从这些组合中,寻找效果最好的超参数组合。
# scoring:模型评估标准。
# n_jobs:并发数量。
# cv:交叉验证折数。
# verbose:输出冗余信息,值越大,输出的信息越多。
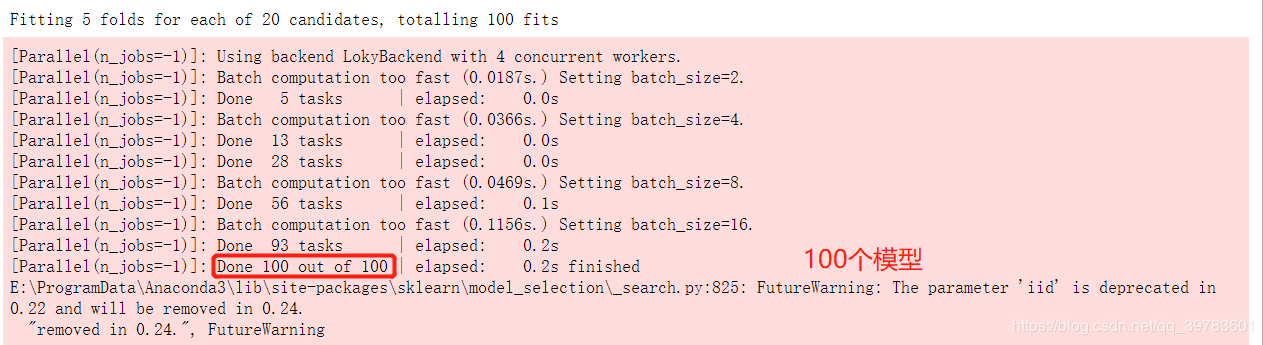
gs = GridSearchCV(estimator=knn, param_grid=grid, scoring="accuracy", n_jobs=-1, cv=5, verbose=10, iid=True)
# cv=5每一种超参数都进行5折交叉验证
gs.fit(X_train, y_train)
GridSearchCV,它存在的意义就是自动调参,只要把参数输进去,就能给出最优化的结果和参数,这个方法适合于小数据集。
GridSearchCV参数说明:
estimator:评估器,即对哪个模型调整超参数。
param_grid:需要检验的超参数组合。从这些组合中,寻找效果最好的超参数组合,值为字典或者列表。
coring:模型评估标准。
n_jobs:并发数量。
cv:交叉验证折数。
verbose:输出冗余信息,值越大,输出的信息越多。
结果:

当网格交叉验证结束后,我们就可以通过GridSearchCV对象的相关属性,来获取最好的参数,分值与模型。
# 最好的分值。
print(gs.best_score_)
# 最好的超参数组合。
print(gs.best_params_)
# 使用最好的超参数训练好的模型。
print(gs.best_estimator_)

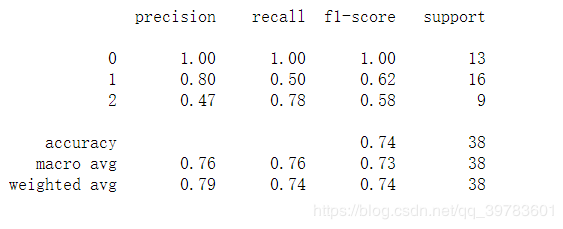
最后,我们使用最好的模型在测试集上进行测试,实现最后的检验。
estimator = gs.best_estimator_
y_hat = estimator.predict(X_test)
print(classification_report(y_test, y_hat))
结果:
练习:
通过网格交叉验证,可以帮助我们完成调参工作,因此,即使我们不太了解超参数的含义,也可以顺利完成调参任务。这种说法正确吗?(B)
A 正确
B 不正确
我们以波士顿房价数据集为例,通过KNN算法实现回归预测。同时,我们使用线性回归算法进行对比。
from sklearn.datasets import load_boston
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression
X, y = load_boston(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)
knn = KNeighborsRegressor(n_neighbors=3, weights="uniform")
knn.fit(X_train, y_train)
print("KNN算法R^2值:", knn.score(X_test, y_test))
lr = LinearRegression()
lr.fit(X_train, y_train)
print("线性回归算法R^2值:", lr.score(X_test, y_test))
结果:

我们可以看到结果KNN算法小于线性回归算法的R²值。
我们发现,使用KNN算法进行回归,效果比线性回归要差很多,但这并不能证明KNN算法是不如线性回归的。
原因在于,线性回归在训练参数时,不是基于距离进行计算的,因此,即使线性回归各个特征的量纲(数量级)不同,也不影响最终的拟合效果(权重会不同)。
不过,KNN是基于距离计算的,如果特征之间的量纲不同,在计算时,量纲较大的特征就会占据主导地位,从而算法会忽略量纲较小的特征,这将会对模型性能造成较大的影响。
实际上,不只是KNN算法,很多算法对特征的数量级都是敏感的,因此,在使用算法之前,我们最好将数据集中的特征转换成相同的量纲,从而消除不同量纲对算法造成的负面影响,我们将这个过程称为 数据标准化。 实际上,即使特征量纲相同,标准化也不会产生负面影响。
在scikit-learn中,常用的标准化方式为均值标准差标准化(StandardScaler)与最小最大值标准化(MinMaxScaler)。
均值标准差标准化 =(每个特征 - 特征的平均值)/ 特征的标准差【特征变为均值为0标准差为1】
最小最大值标准化 = (当前值 - 最小值)/ (最大值 - 最小值)【每个特征缩放到(0,1)这个区间内】
from sklearn.preprocessing import StandardScaler, MinMaxScaler
scaler = [StandardScaler(), MinMaxScaler()]
desc = ["均值标准差标准化", "最小最大值标准化"]
for s, d in zip(scaler, desc):
X_train_scale = s.fit_transform(X_train)
X_test_scale = s.transform(X_test)
knn = KNeighborsRegressor(n_neighbors=3, weights="uniform")
knn.fit(X_train_scale, y_train)
print(d, knn.score(X_test_scale, y_test))
StandardScaler 均值标准差标准化
MinMaxScaler 最小最大值标准化
结果:

我们发现,通过标准化处理之后,模型效果有了显著的提升。
在上例中,我们使用标准化对训练数据进行了转换,然后使用KNN模型对象在转换后的数据上进行拟合。可以说,这是两个步骤。我们虽然可以分别去执行这两个步骤,然而,当数据预处理的工作较多时,可能会涉及更多的步骤(例如多项式扩展,One-Hot编码,特征选择等操作),此时分别执行每个步骤会显得过于繁琐。
流水线(Pipeline类)可以将每个评估器视为一个步骤,然后将多个步骤作为一个整体而依次执行,这样,我们就无需分别执行每个步骤。 例如,在上例中,我们就可以将数据标准化与训练模型两个步骤视为一个整体,一并执行。
流水线具有最后一个评估器的所有方法。 当通过流水线对象调用方法 f
时,会执行这样的过程(假设流水线具有个评估器):
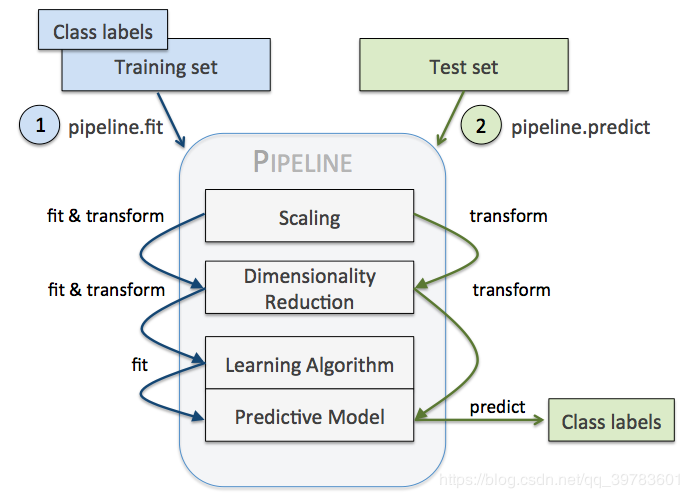
例如,当在流水线上调用fit方法时,将会依次在每个评估器上调用fit_transform方法,前一个评估器将转换之后的结果传递给下一个评估器,直到最后一个评估器调用fit方法为止(最后一个评估器不会调用transform方法)。而当在流水线上调用predict方法时,则会依次在每个评估器上调用transform方法,在最后一个评估器上调用predict方法。
from sklearn.pipeline import Pipeline
X, y = load_boston(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)
# 定义流水线的步骤。类型为一个列表,列表中的每个元素是元组类型,
# 格式为:[(步骤名1,评估器1), (步骤名2, 评估器2),……, (步骤名n, 评估器n)
steps = [("scaler", StandardScaler()), ("knn", KNeighborsRegressor())]
p = Pipeline(steps)
# 设置流水线的参数。所有可用的参数,可以通过get_params获取。
p.set_params(knn__n_neighbors=3, knn__weights="uniform")
p.fit(X_train, y_train)
print(p.score(X_test, y_test))
解析:
knn__ :这里knn两个下划线就是一种命名方法,给knn设置其参数。
结果:
![]()
当样本数量较少时,我们可以使用遍历所有样本的方式,找出最近的K的邻居,然而,如果数据集庞大,这种方式会造成大量的时间开销,此时,我们可以使用KD树的方式来选择K个邻居。
KD树算法中,首先是对训练数据进行建模,构建KD树,然后再根据建好的模型来获取邻近样本数据。
作者:糖潮丽子~辣丽