逻辑回归分类算法

Hazel ·

更新时间:2024-11-11

· 893 次阅读

首先明确，分类问题，"y"的值域一定是有限个，逻辑回归就是根据之前的数据，预测某事件为真的概率值

为什么分类问题不能用线性回归？

对于分类问题，y的取值为0或者1 如果使用线性回归i，那么线性回归模型的输出值可能远大于1或者远小于0 导致代价函数很大 回归模型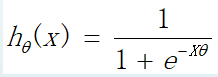

在这里插入图片描述
或者

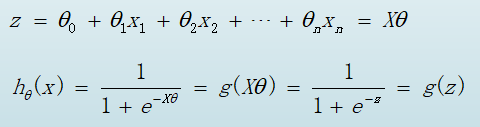
python代码实现

z = numpy.dot(X, theta)
h = 1/(1+numpy.exp(-z))     # exp: e 的多少次方

代价函数

在这里插入图片描述

x1 = X[:, 1]    # 这里X是拼1之后的
x2 = -(theta[0] + theta[1]*x1)/theta[2]

在进行数据拼接之前，需要做特征缩放，使数据标准化

在这里插入图片描述
X = (x-numpy.mean(x)) / numpy.std(x, axis=0, ddof=1) # mean 平均值 std 标准差 ddof 无偏估计

方差表示数据的波动量(稳定程度)
代价函数就是信息墒，信息熵=信息量*概率

逻辑回归代码

'''
逻辑回归
1. 提取数据
2.特征缩放
3.拼接数据抽取规格
4.循环迭代，计算回归模型和代价值，梯度下降
'''
import numpy
import matplotlib.pyplot as plt
if __name__ == '__main__':
    pass
    data = numpy.loadtxt("logicData.txt", delimiter=",")
    x, y = data[:, :-1], data[:, -1]
    # 特征缩放
    x = (x - numpy.mean(x)) / numpy.std(x, axis=0, ddof=1)
    X, Y = numpy.c_[numpy.ones(len(x)), x], numpy.c_[y]
    m, n = X.shape
    alpha, iters = 0.1, 20000
    theta, J = numpy.zeros((n, 1)), numpy.zeros(iters)
    for i in range(iters):
        z = numpy.dot(X, theta)
        h = 1 / (1 + numpy.exp(-z))
        J[i] = (-1 / m) * numpy.sum(Y * numpy.log(h) + (1 - Y) * numpy.log(1 - h))
        grad = (1 / m) * numpy.dot(X.T, h - Y)
        theta -= alpha * grad
    print(theta)
    count = 0   # 精准度
    for i in range(m):
        # numpy.where 条件函数， 如果大于0.5，则返回1
        if numpy.where(h[i] >= 0.5, 1, 0) == y[i]:
            count += 1
    rate = count / m
    print("精准度：", rate)
    # 数据可视化
    plt.subplot(121)
    plt.plot(J)
    plt.subplot(122)
    # 循环画散点
    # for i in range(m):
    #     if y[i] == 1:
    #         plt.scatter(X[i, 1], X[i, 2], c="r", marker=".")
    #     else:
    #         plt.scatter(X[i, 1], X[i, 2], c="g", marker=".")
    # 布尔索引画散点
    plt.scatter(X[Y[:, 0] == 1, 1], X[Y[:, 0] == 1, 2], c="r", marker=".")
    plt.scatter(X[Y[:, 0] == 0, 1], X[Y[:, 0] == 0, 2], c="g", marker=".")
    # 画分类分割线
    x1 = X[:, 1]
    x2 = -(theta[0] + theta[1] * x1) / theta[2]
    plt.plot(x1, x2, c="b")
    plt.show()

作者：Dr_W

逻辑回归回归分类分类算法算法

1024 个赞