【数学知识】非线性方程求解的二分法以及牛顿迭代法
【数学知识】非线性方程求解的二分法以及牛顿迭代法导入包二分法问题1编程作业牛顿迭代法编程作业
本博客不谈及理论推导，只提供代码实现，关于理论推导，大家可以查看其它博客文章。 导入包
本博客不谈及理论推导，只提供代码实现，关于理论推导，大家可以查看其它博客文章。 导入包
import sys
import math
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
二分法
class ConditionError(Exception):
def __init__(self,ErrorInfo):
super().__init__(self)
self.errormsg = ErrorInfo
def __str__(self):
return self.errormsg
def BisectionMethod(f,a,b,err=1e-5,max_iter=100):
'''A root-finding method:Bisection method.
Args
----------
f: callable function
The nonlinear function to be solved.
a,b: float
The initial interval, which satisfies the condition:ab:
raise ConditionError('Wrong interval setup,it must be: a0 and f(b)>0) or (f(a)<0 and f(b)<0):
print("Can't find the root of function as the condition is insurficient!")
n = 1
while n<max_iter:
c = (a+b)/2
print("n={},c={}".format(n,f(c)))
if f(c)==0 or (b-a)/20:
a = c
else:
b = c
print("求解结果：n={},tol={},x0={}".format(n,abs(f(x0)),x0))
tol, iters = abs(f(x0)), n
return x0,tol,iters
问题1
求解方程
(x+5)(x−1)(x−3)=0
(x+5)(x-1)(x-3)=0
(x+5)(x−1)(x−3)=0
求解步骤:
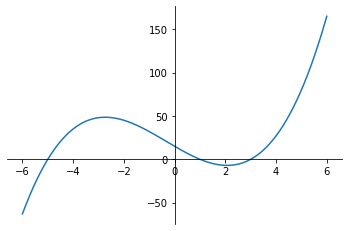
1、画图确定根的大致位置，选择根的初始区间[a,b]
2、使用二分法函数BisectionMethod进行求解
def f(x):
'''Nonlinear function to be solved
$f(x)=(x+5)(x-1)(x-3)$
'''
return (x+5)*(x-1)*(x-3)
x = np.linspace(-6, 6, num = 1000)
y = f(x)
plt.plot(x,y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none') # 将右边 上边的两条边颜色设置为空 其实就相当于抹掉这两条边
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left') # 指定下边的边作为x轴 指定左边的边为y轴
ax.spines['bottom'].set_position(('data', 0)) #指定data设置的bottom(也就是指定的x轴)绑定到y轴的0这个点上
ax.spines['left'].set_position(('data', 0))
原创文章 36获赞 278访问量 7万+
关注
私信
展开阅读全文
作者：YirongChen
