非对称加密RAS算法学习经验

非对称加密&&RAS算法 之前对非对称加密有很大的误解,可以说之前理解的非对称加密都是错误的,经过一位大牛的点拨 (碾压) 充分认识到了自己的错误~,现在重新对非对称加密做一个总结; 之前错误的想法

非对称加密 指的是 传输信息时 拥有公钥/私钥,公钥加密的信息只能使用私钥解密,私钥加密的信息只有公钥能解密~ 仅此而已;

但这是错误的,这是非对称加密的必要条件;但不是充分必要条件;

现阶段我认为的非对称加密

在上面介绍的继续做补充;

非对称加密的通信方式是单向的~
小明对小红发送信息如果小明要保密,小明就必须使用小红的公钥上锁加密.
如果小红对小明发信息使用了小红自己的私钥加密,那么小红发送的信息就可以用公钥解开,但由于公钥是公开的,所以任何人都可以解开,因此
如果小红想要保密的发送信息给小明,应该使用小明的公钥加密给小红;

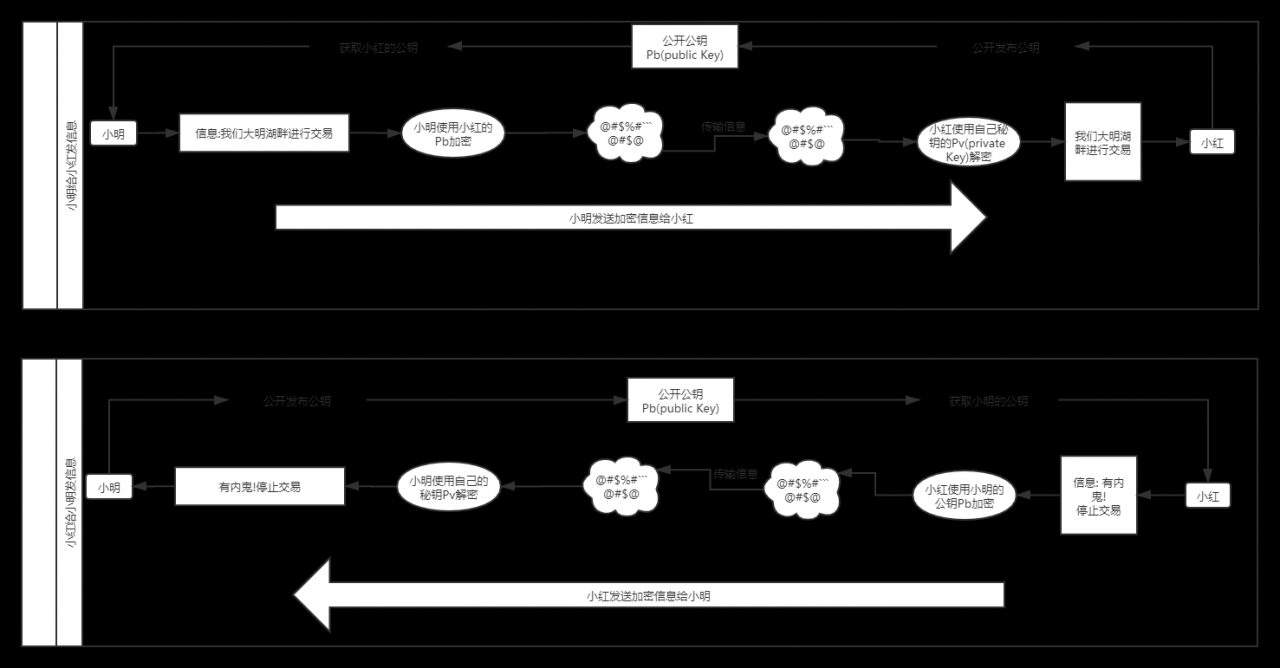
不仅如此,公钥和私钥的关系应该有着这样一个关系:,公钥无法反向推测出私钥(合理时间内);甚至哪怕你的算法源码以及泄露出去,也无法在合理时间内反向破解私钥;

这里有比较成熟的加密算法: RSA、Elgamal、背包算法、Rabin、D-H、ECC（椭圆曲线加密算法）。
其中使用最多的是 RSA 加密算法;

下面谈一谈我对RSA算法的理解;

RSA算法理解学习 预备知识 关于求余的几个公式恒等式 (a+b)%p=(a%p+b%p)%p(a+b)\%p=(a\%p + b\%p)\%p(a+b)%p=(a%p+b%p)%p (a−b)%p=(a%p−b%p+p)%p(a-b)\%p=(a\%p - b\%p + p)\%p(a−b)%p=(a%p−b%p+p)%p (a∗b)%p=(a%p∗b%p+p)%p(a*b)\%p=(a\%p * b\%p + p)\%p(a∗b)%p=(a%p∗b%p+p)%p 模逆元
如果有正整数 n , m ,e 有以下关系恒成立
(m∗n)%e≡1(m*n)\%e≡1(m∗n)%e≡1
那么我们称 m 与 n 互为关于 e的模逆元; 欧拉函数 wiki百科
小于或等于n的正整数中与n互质的数的数目φ(n)函数的作用;
例如:
φ(8) = 4; // 与8互质的数有:1,3,5,7 欧拉-费马定理
对于任何非负整数 a 存在以下恒等关系
aφ(n)%n≡1a^{φ(n)}\%n≡1aφ(n)%n≡1 过程概述 随机选取两个质数 p ,q 令 N = p * q 令 r = φ(N) 随机选取一个数字 e 满足 e<r && e 与 r 互质 求得 e关于 r 的模逆元 d
及存在以下关系
(e⋅d)%r=1 (e·d) \%r = 1(e⋅d)%r=1 此时集合 {e,N}作为公钥分发公开, {d,N}作为私钥自己保存 加密过程:
现加密传输一个小于N的非负整数 ***m***:
n=me%Nn=m^e\%Nn=me%N
得到 密文 ***n***; 解密过程: 得到密文 ***n***:
m=nd%Nm=n^d\%Nm=nd%N
得到 原始信息m; 所有的数据信息都可以转化为Unicode 或者 ascii 码进行传输,重复上述 7加密过程后发送密文即可实现加密传输; 数学解析

首先证明下列两公式成立:
n=me%Nn=m^e\%Nn=me%N
m=nd%Nm=n^d\%Nm=nd%N

将1代入到2得:
m=(me%N)d%Nm=(m^e\%N)^d\%Nm=(me%N)d%N 展开使用乘法表示:
m=[(me%N)∗(me%N)∗⋅⋅⋅∗(me%N)]%Nm=[(m^e\%N)*(m^e\%N)*···*(m^e\%N)]\%Nm=[(me%N)∗(me%N)∗⋅⋅⋅∗(me%N)]%N 根据求余恒等公式3得:
m=[me∗me∗⋅⋅⋅∗me]%N=(me)d%Nm=[m^e*m^e*···*m^e]\%N=(m^e)^d\%Nm=[me∗me∗⋅⋅⋅∗me]%N=(me)d%N 因为 (e*d)%r = 1 && r = φ(N) 得到:(k为系数 关系为: (ed)%r = k 余 1))
m=m(k∗r+1)%N=(mk∗φ(N)+1)%N=(m∗mk∗φ(N))%N=(m∗(mφ(N))k)%Nm=m^{(k*r+1)}\%N=(m^{k*φ(N)+1})\%N = (m*m^{k*φ(N)})\%N= (m*(m^{φ(N)})^k)\%Nm=m(k∗r+1)%N=(mk∗φ(N)+1)%N=(m∗mk∗φ(N))%N=(m∗(mφ(N))k)%N 展开可得:
m={m%N∗[(mφ(N)%N∗mφ(N)%N∗...∗mφ(N)%N)]%N}%Nm=\{m\%N*[(m^{φ(N)}\%N*m^{φ(N)}\%N*...*m^{φ(N)}\%N)]\%N\}\%Nm={m%N∗[(mφ(N)%N∗mφ(N)%N∗...∗mφ(N)%N)]%N}%N 由欧拉-费马定理
mφ(N)%N≡1m^{φ(N)}\%N≡1mφ(N)%N≡1
代入后可得
m=[m%N∗(1∗1∗...∗1)%N]%N=(m%N∗1%N)%N=m%Nm=[m\%N*(1*1*...*1)\%N]\%N=(m\%N*1\%N)\%N=m\%Nm=[m%N∗(1∗1∗...∗1)%N]%N=(m%N∗1%N)%N=m%N
这里发出一个问题:欧拉费马定理指出当m与N互质时公式成立,但是这里m有可能不与N互质,但是等式仍然成立~为什么?特殊的某个值在哪里不成立导致了这一条件? 因为 m < N
m≡m%N得证; 代码求解 //获取公钥 私钥 (即上文中互为模逆元的 e && d) bool getKey(unsigned int * pb,unsigned int* pv,unsigned int modNum) { *pb = modNum; while(judgeRelativelyPrime(*pb,modNum) == false) { *pb = getRandPrimeNum(modNum); //在1~modNum中随机返回一个质数 if(*pb == -1u) return false; } int k = 0; for(;(k*modNum+1)%e !=0;k++) { } if ((k*modNum + 1) % e == 0) *pv = (k*modNum + 1) / e; retrun true; } //加密 unsigned int encryption(unsigned int bigNum,unsigned int pb,unsigned int byt) { return ((unsigned int)pow(byt,pb)) % bigNum; } //解密 unsigned int decryption(unsigned int bigNum,unsigned int pv,unsigned int ecp) { return ((unsigned int)pow(byt,pv)) % bigNum; } 注意事项!

这里的函数只能作为示例,因为现有的RSA算法都是基于大数质数的计算进行加密保护,正是由于此,哪怕知道公钥和算法源码别人也无法咋合理的时间内破解秘钥~
因此需要将 unsigned int 更换为支持超大数据的类型,同时实现大数的加减乘除以及求余即可~

作者：Kim_小星兴

ras 加密 学习 非对称加密