深度学习之RNN、LSTM及正向反向传播原理

 RNN( Recurrent Neural Network 循环(递归)神经网络) 跟人的大脑记忆差不多。我们的任何决定，想法都是根据我们之前已经学到的东西产生的。RNN通过反向传播和记忆机制，能够处理任意长度的序列，在架构上比前馈神经网络更符合生物神经网络的结构，它的产生也正是为了解决这类问题而应用而生的。

    RNN及改进的LSTM等深度学习模型都是基于神经网络而发展的起来的认知计算模型。从原理来看，它们都是源于认知语言学中的“顺序像似性”原理：文字符号与其上下文构成一个“像”，这个“像”可以被认为是符号与符号的组合——词汇，也可以被认为是词汇与词汇的句法关系——依存关系。算法的训练过程，是通过正向和反馈两个过程从训练语料中学习出识别这些“像”的能力，并记录下“像”的模型数据，当输入的新的句子时，算法可以利用存储的模型数据识别出新输入中类似的“像”。

    one to one：

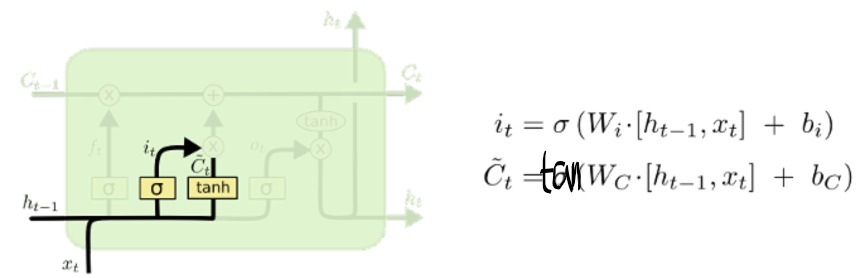
输入和更新

      然后确定什么样的新信息被存放在细胞状态中。这里包含两部分：

        一部分是Sigmoid层，称为“输入门”，它决定我们将要更新什么值；

        另一部分是tanh层，创建一个新的候选值向量~C_t，它会被加入到状态中。

    这样，就能用这两个信息产生对状态的更新。

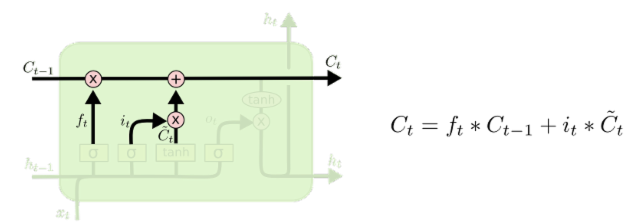
更新细胞状态

    现在是更新旧细胞状态的时间了，C_t-1 更新为 C_t 。前面的步骤已经决定了将会做什么，现在就是实际去完成。把旧状态与 f_t 相乘，丢弃掉我们确定需要丢掉的信息，接着加上i_t*~C_t。这就是新的候选值，根据更新每个状态的程度进行变化。

    在语言模型的例子中，这就是我们实际根据前面的目标，丢弃旧代词的类别信息并添加新的信息的地方。

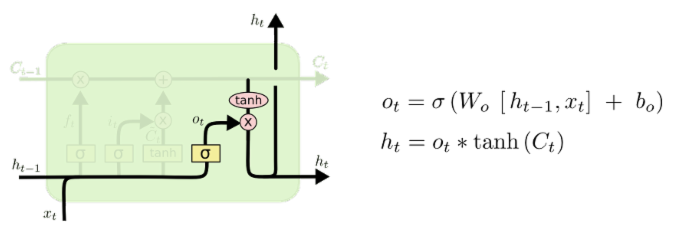
输出信息

    最终需要确定输出什么值。这个输出将会基于细胞状态，但也是一个过滤后的版本。首先，运行一个Sigmoid层来确定细胞状态的哪个部分将输出出去。接着，把细胞状态通过tanh进行处理( 得到一个在 -1~1 之间的值 ) 并将它和Sigmoid门相乘，最终仅仅会输出我们确定输出的那部分。

    与RNN相同，都要最小化损失函数 l(t)。下面用 h(t) 表示当前时刻的隐藏层输出，y(t)表示当前时刻的输出标签，参考在后面的代码使用的是平方差损失函数，则损失函数被表示为：

    全局化的损失函数如下：

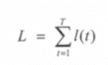
通过梯度法，实现损失函数最小化参数估计。由于损失函数 l(t) 依赖于隐藏层 h(t) 和 输出层 y(t)，根据链式法则，得到下式：

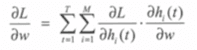
    这里w是模型权重的标量，M是记忆单元的长度，i是隐藏层的第i个记忆单元，h_i(t)是一个标量，表示隐藏层第i个记忆单元的输出。由于网络随时间正向传播，改变h_i(t) 将不会影响到先于时间t的损失。

    引入一个变量L(t)，它表示了第i步开始到结束的损失。

    上述函数变更如下：

    求解这个式子的最优化结果：

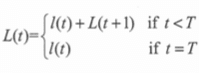
    联立这个式子的最优化结果：

    上式右侧的第一项来自简单的损失函数l(t)的时间t的导数。第二项的本质是一个循环项，它表明，计算当前节点的导数的信息时，需要下一节点的导数信息。这与RNN网络反向传播的过程相同，这里不再详细说明。

学习 反向传播 深度学习 rnn lstm