Python实现二叉搜索树的删除功能
二叉搜索树(二叉查找树,Binary Search Tree)又称为排序二叉树、有序二叉树。
二叉搜索树的实现可以参考:https://blog.csdn.net/weixin_43790276/article/details/105753543
本文使用 Python 实现二叉搜索树的删除功能,在此之前必须先知道二叉搜索树的特性:
1. 如果二叉树的左子树不为空,则左子树上所有节点的值均小于它的根节点的值。
2. 如果二叉树的右子树不为空,则右子树上所有节点的值均大于它的根节点的值。
3. 如果独立地看,左子树、右子树也分别为二叉搜素树。
一、准备二叉搜索树类
在实现二叉搜索树的删除功能前,先实现一个二叉搜索树的类 SearchBinaryTree 。
# coding=utf-8
class Node(object):
"""节点类"""
def __init__(self, data, left_child=None, right_child=None):
self.data = data
self.parent = None
self.left_child = left_child
self.right_child = right_child
class SearchBinaryTree(object):
"""二叉树类"""
def __init__(self):
self.__root = None
self.prefix_branch = '├'
self.prefix_trunk = '|'
self.prefix_leaf = '└'
self.prefix_empty = ''
self.prefix_left = '─L─'
self.prefix_right = '─R─'
def is_empty(self):
return not self.__root
@property
def root(self):
return self.__root
@root.setter
def root(self, value):
if isinstance(value, Node):
node = value
else:
node = Node(value)
self.__root = node
def show_tree(self):
if self.is_empty():
print('空二叉树')
return
print('-' * 20)
print(self.__root.data)
self.__print_tree(self.__root)
print('-' * 20)
def insert(self, root, value):
"""二叉搜索树插入节点-递归"""
if isinstance(value, Node):
node = value
else:
node = Node(value)
if self.is_empty():
self.root = node
return
if root is None:
root = node
elif node.data root.data:
root.right_child = self.insert(root.right_child, value)
root.right_child.parent = root
return root
def __print_tree(self, node, prefix=None):
if prefix is None:
prefix = ''
prefix_left_child = ''
else:
prefix = prefix.replace(self.prefix_branch, self.prefix_trunk)
prefix = prefix.replace(self.prefix_leaf, self.prefix_empty)
prefix_left_child = prefix.replace(self.prefix_leaf, self.prefix_empty)
if self.has_child(node):
if node.right_child is not None:
print(prefix + self.prefix_branch + self.prefix_right + str(node.right_child.data))
if self.has_child(node.right_child):
self.__print_tree(node.right_child, prefix + self.prefix_branch + ' ')
else:
print(prefix + self.prefix_branch + self.prefix_right)
if node.left_child is not None:
print(prefix + self.prefix_leaf + self.prefix_left + str(node.left_child.data))
if self.has_child(node.left_child):
prefix_left_child += ' '
self.__print_tree(node.left_child, self.prefix_leaf + prefix_left_child)
else:
print(prefix + self.prefix_leaf + self.prefix_left)
def has_child(self, node):
return node.left_child is not None or node.right_child is not None
def __str__(self):
return str(self.__class__)
上面的代码实现了一个节点类 Node,实现了二叉搜索树的类 SearchBinaryTree。在 SearchBinaryTree 中,实现了判断二叉搜索树是否为空的 is_empty() 方法、一对供实例对象调用的 root() 方法、按树形结构打印二叉搜索树的 show_tree() 方法和添加数据到二叉搜索树中的 insert(root, value)方法。
现在先在树中添加一些节点,供后面的删除方法使用。
if __name__ == '__main__':
tree = SearchBinaryTree()
data = [50, 77, 55, 29, 10, 30, 66, 80, 51, 18, 90, 78, 79]
for i in data:
tree.insert(tree.root, i)
tree.show_tree()
运行结果:
--------------------
50
├─R─77
| ├─R─80
| | ├─R─90
| | └─L─78
| | ├─R─79
| | └─L─
| └─L─55
| ├─R─66
| └─L─51
└─L─29
├─R─30
└─L─10
├─R─18
└─L─
--------------------
添加数据后的二叉搜索树如下图:
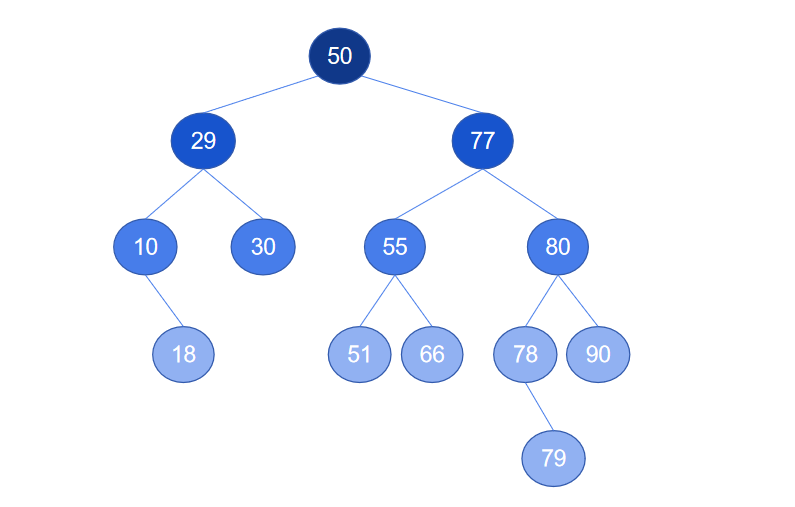
添加完成节点后,继续准备删除节点时需要使用到的方法。返回二叉搜索树的高度的方法 height(root),用于判断被删除的节点在树的第几层。在二叉搜索树中查找节点的方法 search(root, data),要从二叉搜索树中删除节点,首先要保证节点是属于二叉搜索树的,所以先搜索节点是否在二叉搜索树中。返回二叉搜索树中值最大的节点的方法 get_max(root) 和返回值最小的节点的方法 get_min(root) ,用于寻找被删除节点的前继节点或后继节点。
def height(self, root):
"""二叉树的深度"""
if root.data is None:
return 0
if root.left_child is None and root.right_child is None:
return 1
if root.left_child is not None and root.right_child is None:
return 1 + self.height(root.left_child)
if root.left_child is None and root.right_child is not None:
return 1 + self.height(root.right_child)
if root.left_child is not None and root.right_child is not None:
return 1 + max(self.height(root.left_child), self.height(root.right_child))
def search(self, root, data):
"""二叉搜索树的查询操作"""
if root is None:
return
if root.data == data:
return root
elif data root.data:
return self.search(root.right_child, data)
def get_max(self, root):
"""查找二叉搜索树值最大的节点"""
if root.right_child:
return self.get_max(root.right_child)
else:
return root
def get_min(self, root):
"""查找二叉搜索树值最小的节点"""
if root.left_child:
return self.get_min(root.left_child)
else:
return root
二、二叉搜索树删除节点
如果被删除的节点是叶节点,比较好办,找到这个节点,然后删除。如果被删除的节点不是叶节点,节点有左子树或右子树,或两者都有,删除节点后,左子树和右子树会跟着节点一起从树中“断”掉,那就不仅仅是删除节点了,而是把子树给全部删除了。所以,删除非叶节点时,必须从子树中选择一个节点来填补被删除的节点位置,避免树的断裂,也避免“牵连”到其他的节点,还要保证删除节点后的二叉树依然是一棵二叉搜索树,满足二叉搜索树的特性。
那怎么实现删除呢?如何保证删除节点后的二叉树还是二叉搜索树?由简到繁,根据被删除节点是否有左右子树,二叉搜索树的删除可以分为三种情况,被删除节点为叶节点、被删除节点只有一棵子树和被删除节点有两棵子树。
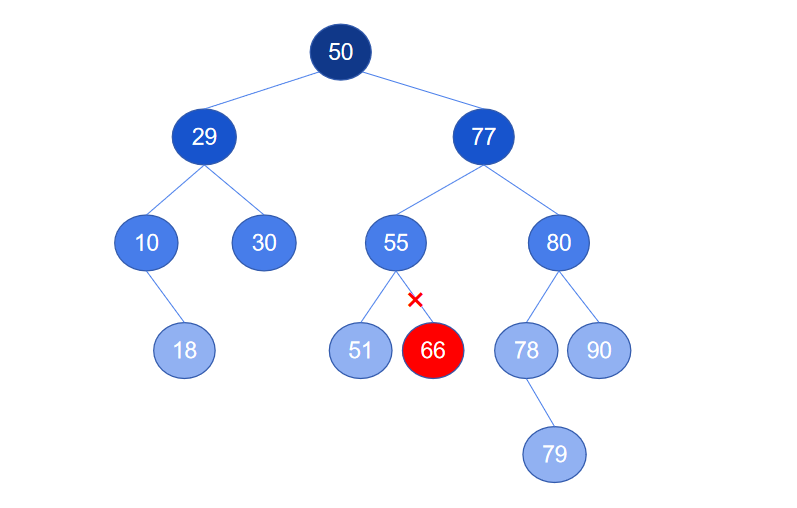
1. 被删除节点为叶节点,即被删除节点没有左子树和右子树。删除叶节点后,不会破坏整棵树的结构,只要找到此节点,然后将节点从二叉树中“断开”(父节点的指针指向空)即可。在上面添加数据后的二叉搜索树中,随机选一个叶节点,如 66。
def _delete_no_child(self, node):
"""删除叶节点"""
if node == self.root:
self.root = None
return
if node == node.parent.left_child:
node.parent.left_child = None
else:
node.parent.right_child = None
node.parent = None
_delete_no_child(node): 删除叶节点的方法。这个方法只属于删除的部分功能,所以在前面加一个下划线,表示等删除功能完全实现后,不会再直接使用。
node = tree.search(tree.root, 66)
tree._delete_no_child(node)
tree.show_tree()
运行结果:
--------------------
50
├─R─77
| ├─R─80
| | ├─R─90
| | └─L─78
| | ├─R─79
| | └─L─
| └─L─55
| ├─R─
| └─L─51
└─L─29
├─R─30
└─L─10
├─R─18
└─L─
--------------------
删除节点 66 后的二叉搜索树结构如下图。

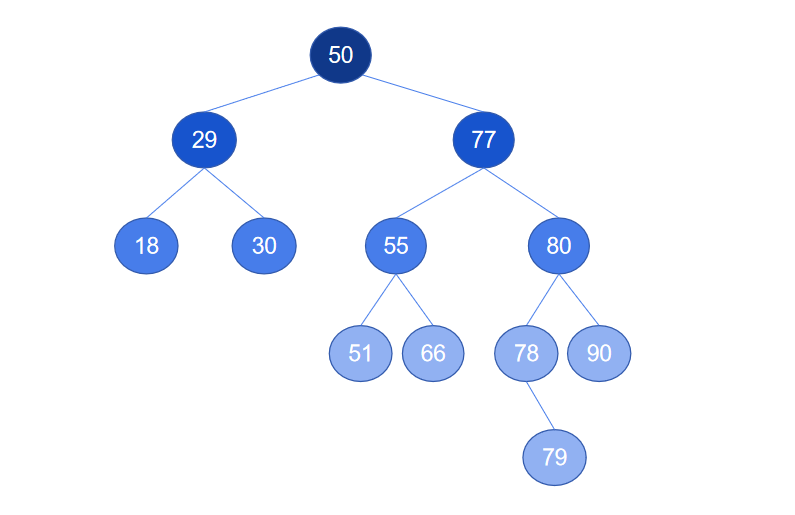
2. 被删除节点只有一棵子树,即被删除节点只有左子树或只有右子树。删除节点后,为了保证节点的子树不被“牵连”,要将节点的子树进行“补位”。如删除下图中的节点 10,被删除节点是其父节点的左子节点,被删除节点有右子树,则删除节点后,直接将被删除节点的右子树补位成为其父节点的左子树。

def _delete_one_child(self, node):
"""删除有一个子节点的节点"""
if node.left_child:
if node.parent and node.parent.left_child == node:
node.left_child.parent = node.parent
node.parent.left_child = node.left_child
elif node.parent and node.parent.right_child == node:
node.left_child.parent = node.parent
node.parent.right_child = node.left_child
else:
self.root = node.left_child
node.left_child.parent = None
node.left_child = None
else:
if node.parent and node.parent.left_child == node:
node.right_child.parent = node.parent
node.parent.left_child = node.right_child
elif node.parent and node.parent.right_child == node:
node.right_child.parent = node.parent
node.parent.right_child = node.right_child
else:
self.root = node.right_child
node.right_child.parent = None
node.right_child = None
node.left_child = None
node.parent = None
_delete_one_child(node): 删除只有一棵子树的节点。同理,这个方法也只属于删除的部分功能,所以在前面加一个下划线,表示删除功能完全实现后,不会直接使用。
node = tree.search(tree.root, 10)
tree._delete_one_child(node)
tree.show_tree()
运行结果:
--------------------
50
├─R─77
| ├─R─80
| | ├─R─90
| | └─L─78
| | ├─R─79
| | └─L─
| └─L─55
| ├─R─66
| └─L─51
└─L─29
├─R─30
└─L─18
--------------------
删除节点 10 后的二叉搜索树结构如下图。
3. 被删除节点有两棵子树,即被删除节点同时有左子树和右子树。删除节点后,为了避免两棵子树从树中“断裂”,必须找到一个节点来填补被删除节点的位置。如删除下图中的节点 77,必须找一个节点来补位,否则两棵子树也会被删除。
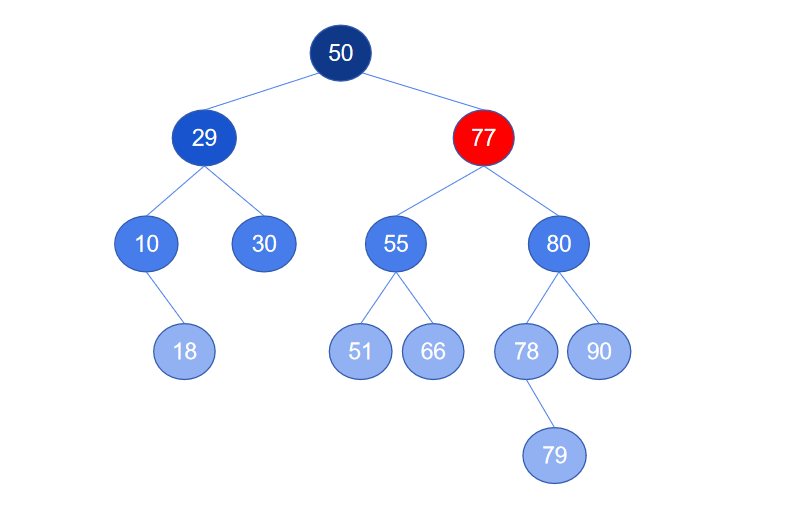
为了保证删除节点后二叉树任然是一棵二叉搜索树,补位节点有两种选择方式,选择被删除节点的前继节点或后继节点,前继节点一定存在左子树中,后继节点一定存在右子树中,选择两种方式都可以,本文选择后继节点。
那什么是后继节点和前继节点?如果将二叉搜索树中的节点按存储的数值的大小升序排列,排在当前节点的后一个节点就是后继节点,排在当前节点的前一个节点就是前继节点。节点 77 的后继节点是 88。
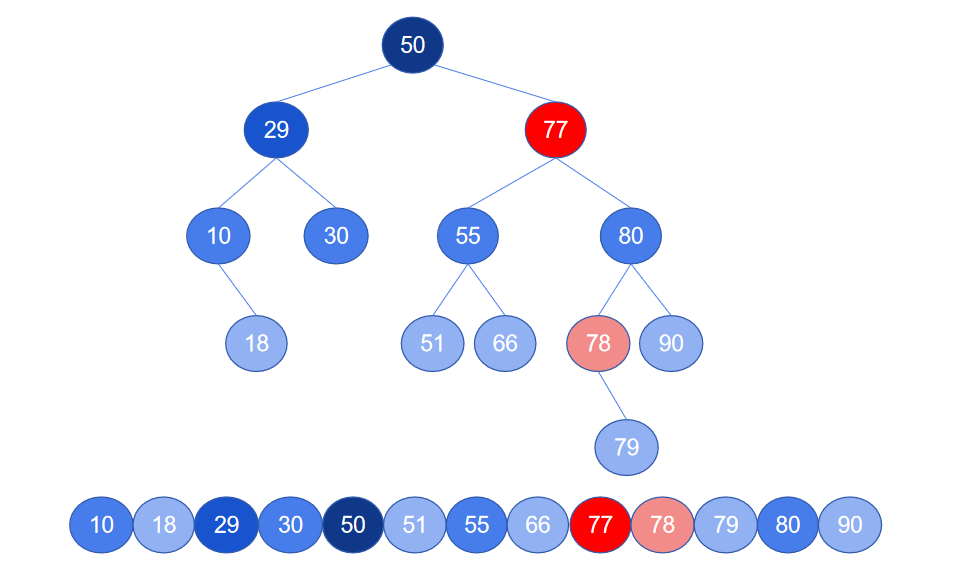
将节点删除后,找到它的后继节点,将后继节点补位到被删除节点的位置,这样就保证了被删除节点的两棵子树没有断裂。但是还没有完,后继节点补位之后,相当于是将后继节点从它原来的位置删除了。节点 78 补位到 77 的位置后,相当于将节点 78 从原来的位置删除了。
所以还要对后继节点进行处理,后继节点可能是叶节点,可以用情况1,后继节点可能有右子树,可以用情况2,如节点 78,后继节点不可能有左子树,不用考虑。
为什后继节点一定没有左子树?假设后继节点有左子树,根据二叉搜索树的特性,后继节点的值比当前节点大,后继节点一定在当前节点的右子树中,而后继节点的左子树中的节点值要小于后继节点的值,这样,就存在比当前节点大又比后继节点小的节点,与后继节点的定义矛盾,所以假设不成立。
到这里,删除节点 77 分为两步,第一步是找到后继节点 78,将节点 78 补位到 77 的位置,第二步是删除节点 78 。

def delete(self, value):
"""二叉搜索树删除节点"""
if self.height(self.root) >= 1:
node_delete = self.search(self.root, value)
if node_delete:
self._delete(node_delete)
else:
raise KeyError("Error, value not in this tree")
else:
raise KeyError("Error, value not in this tree")
def _delete(self, node):
"""删除节点"""
if not node.left_child and not node.right_child:
self._delete_no_child(node)
elif node.left_child and not node.right_child or not node.left_child and node.right_child:
self._delete_one_child(node)
else:
rear_node = self.get_min(node.right_child)
node.data = rear_node.data
self._delete(rear_node)
_delete(node): 删除节点的方法。该方法中通过 get_min() 方法找到当前节点的后继节点 rear_node ,然后进行补位操作。而删除后继节点的操作,只要递归一次就可以,因为删除后继节点的方法一定属于前面的两种情况之一。
delete(node): 删除节点的通用方法。前面提过,要删除节点,首先节点要属于当前二叉搜索树。所以无法指定节点来删除,只能根据节点中存储的值,先在树中进行搜索,找到了再执行删除操作。
tree.delete(77)
tree.show_tree()
运行结果:
--------------------
50
├─R─78
| ├─R─80
| | ├─R─90
| | └─L─79
| └─L─55
| ├─R─66
| └─L─51
└─L─29
├─R─30
└─L─10
├─R─18
└─L─
--------------------
删除节点 77 后的二叉搜索树结构如下图。

三、完整代码
# coding=utf-8
class Node(object):
"""节点类"""
def __init__(self, data, left_child=None, right_child=None):
self.data = data
self.parent = None
self.left_child = left_child
self.right_child = right_child
class SearchBinaryTree(object):
"""二叉树类"""
def __init__(self):
self.__root = None
self.prefix_branch = '├'
self.prefix_trunk = '|'
self.prefix_leaf = '└'
self.prefix_empty = ''
self.prefix_left = '─L─'
self.prefix_right = '─R─'
def is_empty(self):
return not self.__root
@property
def root(self):
return self.__root
@root.setter
def root(self, value):
if isinstance(value, Node):
node = value
else:
node = Node(value)
self.__root = node
def show_tree(self):
if self.is_empty():
print('空二叉树')
return
print('-' * 20)
print(self.__root.data)
self.__print_tree(self.__root)
print('-' * 20)
def insert(self, root, value):
"""二叉搜索树插入节点-递归"""
if isinstance(value, Node):
node = value
else:
node = Node(value)
if self.is_empty():
self.root = node
return
if root is None:
root = node
elif node.data root.data:
root.right_child = self.insert(root.right_child, value)
root.right_child.parent = root
return root
def delete(self, value):
"""二叉搜索树删除节点"""
if self.height(self.root) >= 1:
node_delete = self.search(self.root, value)
if node_delete:
self._delete(node_delete)
else:
raise KeyError("Error, value not in this tree")
else:
raise KeyError("Error, value not in this tree")
def _delete(self, node):
"""删除节点"""
if not node.left_child and not node.right_child:
self._delete_no_child(node)
elif node.left_child and not node.right_child or not node.left_child and node.right_child:
self._delete_one_child(node)
else:
rear_node = self.get_min(node.right_child)
node.data = rear_node.data
self._delete(rear_node)
def _delete_no_child(self, node):
"""删除叶节点"""
if node == self.root:
self.root = None
return
if node == node.parent.left_child:
node.parent.left_child = None
else:
node.parent.right_child = None
node.parent = None
def _delete_one_child(self, node):
"""删除有一个子节点的节点"""
if node.left_child:
if node.parent and node.parent.left_child == node:
node.left_child.parent = node.parent
node.parent.left_child = node.left_child
elif node.parent and node.parent.right_child == node:
node.left_child.parent = node.parent
node.parent.right_child = node.left_child
else:
self.root = node.left_child
node.left_child.parent = None
node.left_child = None
else:
if node.parent and node.parent.left_child == node:
node.right_child.parent = node.parent
node.parent.left_child = node.right_child
elif node.parent and node.parent.right_child == node:
node.right_child.parent = node.parent
node.parent.right_child = node.right_child
else:
self.root = node.right_child
node.right_child.parent = None
node.right_child = None
node.left_child = None
node.parent = None
def height(self, root):
"""二叉树的深度"""
if root.data is None:
return 0
if root.left_child is None and root.right_child is None:
return 1
if root.left_child is not None and root.right_child is None:
return 1 + self.height(root.left_child)
if root.left_child is None and root.right_child is not None:
return 1 + self.height(root.right_child)
if root.left_child is not None and root.right_child is not None:
return 1 + max(self.height(root.left_child), self.height(root.right_child))
def search(self, root, data):
"""二叉搜索树的查询操作"""
if root is None:
return
if root.data == data:
return root
elif data root.data:
return self.search(root.right_child, data)
def get_max(self, root):
"""查找二叉搜索树值最大的节点"""
if root.right_child:
return self.get_max(root.right_child)
else:
return root
def get_min(self, root):
"""查找二叉搜索树值最小的节点"""
if root.left_child:
return self.get_min(root.left_child)
else:
return root
def __print_tree(self, node, prefix=None):
if prefix is None:
prefix = ''
prefix_left_child = ''
else:
prefix = prefix.replace(self.prefix_branch, self.prefix_trunk)
prefix = prefix.replace(self.prefix_leaf, self.prefix_empty)
prefix_left_child = prefix.replace(self.prefix_leaf, self.prefix_empty)
if self.has_child(node):
if node.right_child is not None:
print(prefix + self.prefix_branch + self.prefix_right + str(node.right_child.data))
if self.has_child(node.right_child):
self.__print_tree(node.right_child, prefix + self.prefix_branch + ' ')
else:
print(prefix + self.prefix_branch + self.prefix_right)
if node.left_child is not None:
print(prefix + self.prefix_leaf + self.prefix_left + str(node.left_child.data))
if self.has_child(node.left_child):
prefix_left_child += ' '
self.__print_tree(node.left_child, self.prefix_leaf + prefix_left_child)
else:
print(prefix + self.prefix_leaf + self.prefix_left)
def has_child(self, node):
return node.left_child is not None or node.right_child is not None
def __str__(self):
return str(self.__class__)
if __name__ == '__main__':
tree = SearchBinaryTree()
data = [50, 77, 55, 29, 10, 30, 66, 80, 51, 18, 90, 78, 79]
for i in data:
tree.insert(tree.root, i)
# tree.show_tree()
# node = tree.search(tree.root, 66)
# tree._delete_no_child(node)
# tree.show_tree()
# node = tree.search(tree.root, 10)
# tree._delete_one_child(node)
# tree.show_tree()
tree.delete(77)
tree.show_tree()

 Python碎片
Python碎片
 原创文章 123获赞 320访问量 21万+
关注
私信
展开阅读全文
原创文章 123获赞 320访问量 21万+
关注
私信
展开阅读全文
作者:Python碎片