Crypto 2020网鼎杯 you raise me up Writeup （离散对数）
关键点：离散对数、同余运算
知识点：Antigonae整理的相关概念
看不懂-.-以后再研究，简单理解为：
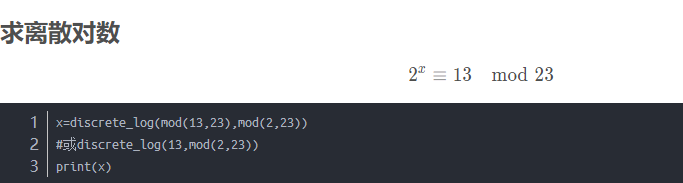
普通对数为 a ** x=b (求x=logab) 离散对数为 a ** x=b % p先会用SageMath~
题目#!/usr/bin/env python
# -*- coding: utf-8 -*-
from Crypto.Util.number import *
import random
n = 2 ** 512
m = random.randint(2, n-1) | 1
c = pow(m, bytes_to_long(flag), n)
print 'm = ' + str(m)
print 'c = ' + str(c)
# m = 391190709124527428959489662565274039318305952172936859403855079581402770986890308469084735451207885386318986881041563704825943945069343345307381099559075
# c = 6665851394203214245856789450723658632520816791621796775909766895233000234023642878786025644953797995373211308485605397024123180085924117610802485972584499
解题
乍一看以为是RSA，但关系并不大，整理下：
已知 c,m,n, c=(m**d)%n
求 d
即 c 与 m ** d 对模n同余，或者说 (c-m**d) % n=0
写sage脚本：
d=discrete_log(c,mod(m,n))
print (d)
再就是flag了
print libnum.n2s(d)
以上~
SageMath相关官网点我
学习SAGE(SAGEMATH)密码学基本使用方法
主要参考的文章：
SAGE(SAGEMATH)密码学基本使用方法
龙雪
原创文章 4获赞 2访问量 1682
关注
私信
展开阅读全文
作者：龙雪
