堆排序——Java与Go实现
概念分析
对于一个深度为k,有n个节点的二叉树,其所有的结点与深度为k的满二叉树对应的编号一样,则称之为完全二叉树。 数组如何转成完全二叉树?
举个栗子,有一个数组arr = {1,2,3,4,5},那我们可以将其构建为以下的二叉树
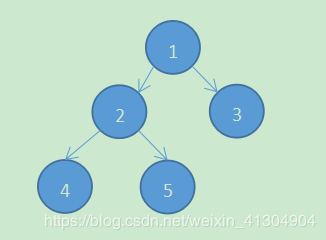
那么我们从这个图可以看出,数组里面下标0对应根结点,之后所有结点的左子结点对应的下标为 2 * n + 1,n就是该分支节点的下标索引,右子结点对应的就是 2 * n + 2;以此规则,虽然该数组依然是个数组,但是我们从逻辑上将其构建成了完全二叉树。 大顶堆和小顶堆是什么?
大顶堆和小顶堆都是类似完全二叉树,或者其就是一个完全二叉树,不过其具有一个特点:父结点必然大于或者小于其左子结点或者其右子结点。以完全二叉树分析来看,就是其根节点是最大或者最小的元素。 如何将完全二叉树构建成大顶堆或者小顶堆
1) 我们首先从最后一个分支节点开始,如上述的例子,最后一个分支节点是2,以此类推,如果数组为{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13},那么其最后一个分支节点就是6(因为13对应的下标12,,1 2 = 2 * 5 + 2, 11 = 2 * 5 + 1,最后两个结点的父结点自然是最后一个分支结点 )
2) 我们将最后一个分支结点与其左子结点和其右子结点比较,选出最小或者最大的作为分支结点的值 之后我们选择该分支结点的前一个分支结点再进行排序,知道我们排到根节点,此时所有的分支结点的值都小于或者大于其左右子结点,此时,该完全二叉树构建成为了堆。 如何进行排序?
我们将堆顶元素与最后一个元素换位置,如上,我们将1与5换位置,之后将1丢弃。此时堆不满足最小堆,我们再将其构建为小顶堆,再进行换位置,此时被丢弃的元素其实是在数组的最后一个,最后小顶堆排序下来的就是一个降序的有序数组。
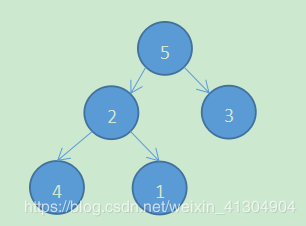

此时数组变成:

当我们重复上述步骤的时候,最后的结果就会是:5 4 3 2 1 代码实现
作者:一个非常帅气的骚包
堆排序是使用堆这种数据结构进行排序的方法。(好像是废话)
思路分析 首先,我们将待排序的数组看作一个完全二叉树 将此二叉树转成大顶堆或者小顶堆 将堆顶元素与堆的最后一个元素互换,之后丢弃最后一个元素 重复第二步与第三步,知道堆只剩一个堆顶 具体解析 什么是完全二叉树?对于一个深度为k,有n个节点的二叉树,其所有的结点与深度为k的满二叉树对应的编号一样,则称之为完全二叉树。 数组如何转成完全二叉树?
举个栗子,有一个数组arr = {1,2,3,4,5},那我们可以将其构建为以下的二叉树

那么我们从这个图可以看出,数组里面下标0对应根结点,之后所有结点的左子结点对应的下标为 2 * n + 1,n就是该分支节点的下标索引,右子结点对应的就是 2 * n + 2;以此规则,虽然该数组依然是个数组,但是我们从逻辑上将其构建成了完全二叉树。 大顶堆和小顶堆是什么?
大顶堆和小顶堆都是类似完全二叉树,或者其就是一个完全二叉树,不过其具有一个特点:父结点必然大于或者小于其左子结点或者其右子结点。以完全二叉树分析来看,就是其根节点是最大或者最小的元素。 如何将完全二叉树构建成大顶堆或者小顶堆
1) 我们首先从最后一个分支节点开始,如上述的例子,最后一个分支节点是2,以此类推,如果数组为{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13},那么其最后一个分支节点就是6(因为13对应的下标12,,1 2 = 2 * 5 + 2, 11 = 2 * 5 + 1,最后两个结点的父结点自然是最后一个分支结点 )
2) 我们将最后一个分支结点与其左子结点和其右子结点比较,选出最小或者最大的作为分支结点的值 之后我们选择该分支结点的前一个分支结点再进行排序,知道我们排到根节点,此时所有的分支结点的值都小于或者大于其左右子结点,此时,该完全二叉树构建成为了堆。 如何进行排序?
我们将堆顶元素与最后一个元素换位置,如上,我们将1与5换位置,之后将1丢弃。此时堆不满足最小堆,我们再将其构建为小顶堆,再进行换位置,此时被丢弃的元素其实是在数组的最后一个,最后小顶堆排序下来的就是一个降序的有序数组。


此时数组变成:
当我们重复上述步骤的时候,最后的结果就会是:5 4 3 2 1 代码实现
思路分析一大堆,还是直接上代码吧
首先java进行堆排序的升序排序:
package tree;
import java.util.Arrays;
import java.util.Random;
public class HeapSort {
public static void main(String[] args) {
// 建立一个无序的顺序存储二叉树
int[] arr = new int[80000];
Random random = new Random();
for (int i = 0; i = 0; i--){
adjustHeap(arr, i, arr.length);
}
for (int j = arr.length - 1; j>= 0; j --){
// 换位置
int temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
// 每次j会自减 那么就相当于把数组的最后一个元素丢弃了
adjustHeap(arr, 0, j);
}
}
/**
*
* @param arr 待排序的数组
* @param i 最下面的分支节点
* @param length 需要调整的长度
*/
public static void adjustHeap(int[] arr, int i, int length){
// 记录一下最开始进入循环之前的分支节点的值
int temp = arr[i];
// 取左子孩子节点
for (int k = i * 2 + 1; k < length; k = 2 * k + 1){
// 如果当前分支节点有右孩子,并且右孩子比左孩子大,那么我们去比较右孩子
if (k + 1 arr[k]){
k++;
}
// 如果孩子节点比该父节点大,父节点换成孩子节点
if (arr[k] > temp){
arr[i] = arr[k];
i = k; // 相当于递归,再去查该孩子节点的孩子节点
}else {
break;
}
}
arr[i] = temp;
}
}
之后是Go实现的小顶堆的降序排序:
package main
import (
"fmt"
"time"
"math/rand"
)
var count int
func main(){
arr := make([]int, 80000)
t := time.Now()
fomat := t.UnixNano()
rand.Seed(fomat)
for i := 0; i = 0; i--{
adjust(arr, i, len(arr))
}
// 现在原本的二叉树已经是一个小顶堆
for j := len(arr) - 1; j > 0; j--{
// 换位置 没什么好说的
temp := arr[j]
arr[j] = arr[0]
arr[0] = temp
// 调整根结点为小顶堆
// 为什么不重新从最后一个分支节点开始呢?
// 因为此时根结点和最后一个元素换位置,那么根结点肯定大于他的左右子节点,我们将根结点对应的树调整为小顶堆即可
// 每次传入的长度要减少,因为我们逻辑上来说是将最后一个分支节点去除
adjust(arr, 0, j)
}
}
// 将二叉树转成小顶堆
func adjust(arr []int, i, length int){
// 先用一个变量记录i位置的值
// i位置的值代表什么呢? 代表当前分支节点在数组中的坐标
// 我们要拿当前分支节点作为根结点,将分支节点看作一个二叉树
// 将这个小树苗转成小顶堆,所以需要比较左右子节点与分支节点的值
temp := arr[i]
for k := 2 * i + 1; k < length; k = k * 2 + 1{
// 如果右子结点比左子结点小
if (k + 1 < length && arr[k + 1] < arr[k]){
k++
}
if (arr[k] < temp){
arr[i] = arr[k]
i = k
}else{
break
}
}
// 此时这个子树里面是含有两个重复的数的 因为我们一直在使用arr[i] = arr[k]
// 所以此时我们将最后的i的对应的值赋值为temp
arr[i] = temp
}
效率分析
Java:
![]()
Go:
![]()
可以看到 堆排序在效率上还是狠给力的。
just do it!
作者:一个非常帅气的骚包
相关文章
Xena
2020-07-03
Liana
2021-04-13
Tamara
2020-01-07
Miki
2020-07-14
Olinda
2023-07-21
Mathilda
2023-07-21
Oria
2023-07-21
Yvonne
2023-07-21
Elsa
2023-07-21
Gilana
2023-07-21
Maleah
2023-07-21
Oceana
2023-07-21
Tallulah
2023-07-21
Fern
2023-07-21
Trixie
2023-07-21
Madeleine
2023-07-21
Aggie
2023-07-21
Xylona
2023-07-21
Rose
2023-07-22