动手学深度学习Pytorch Task05

Jillian ·

更新时间:2024-11-13

· 691 次阅读

本节课内容，卷积神经网络基础、LeNet、卷积神经网络进阶

一、卷积神经网络基础

二维互相关运算：二维互相关运算的输入是一个二维输入数组和一个二维核数组，输出也是一个二维数组，其中核数组通常称为卷积核或过滤器。卷积核的尺寸通常小于输入数组，卷积核在输入数组上滑动，在每个位置上，卷积核与该位置处的输入子数组按元素相乘并求和，得到输出数组中相应位置的元素。下图展示了一个互相关运算的例子，阴影部分分别是输入的第一个计算区域、核数组以及对应的输出。
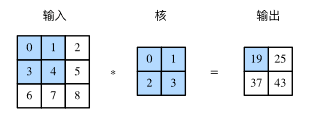
在这里插入图片描述
二维卷积层：二维卷积层将输入和卷积核做互相关运算，并加上一个标量偏置来得到输出。卷积层的模型参数包括卷积核和标量偏置。

互相关运算和卷积运算：卷积层得名于卷积运算，但卷积层中用到的并非卷积运算而是互相关运算。我们将核数组上下翻转、左右翻转，再与输入数组做互相关运算，这一过程就是卷积运算。由于卷积层的核数组是可学习的，所以使用互相关运算与使用卷积运算并无本质区别。

特征图和感受野：二维卷积层输出的二维数组可以看作是输入在空间维度（宽和高）上某一级的表征，也叫特征图。影响x元素的前向计算的所有可能输入区域（可能大于输入的实际尺寸）叫做x的感受野。

padding：padding是指在输入高和宽的两侧填充元素（通常是0元素），图2里我们在原输入高和宽的两侧分别添加了值为0的元素。下图中外圈的0即为填充。
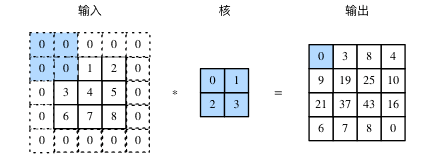
在这里插入图片描述
步幅：在互相关运算中，卷积核在输入数组上滑动，每次滑动的行数与列数即是步幅（stride）。此前我们使用的步幅都是1，下图展示了在高上步幅为3、在宽上步幅为2的二维互相关运算。

一般来说，一般来说，当高的两侧一共填充ph行，在宽的两侧一共填充pw列，高上步幅为是Sh，宽上步幅为Sw时，输出形状为：

多输入通道：卷积层的输入可以包含多个通道，下图展示了一个含2个输入通道的二维互相关计算的例子。
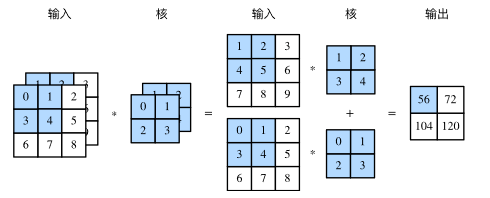
在这里插入图片描述
多输出通道：当有多个卷积核时，会有多输出通道。

1x1卷积层：1x1卷积核可在不改变高宽的情况下，调整通道数。1x1卷积核不识别高和宽维度上相邻元素构成的模式，其主要计算发生在通道维上。假设我们将通道维当作特征维，将高和宽维度上的元素当成数据样本，那么1x1卷积层的作用与全连接层等价。
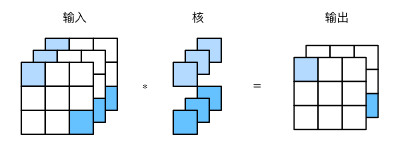
在这里插入图片描述
卷积层的简单实现：

conv2d = nn.Conv2d(in_channels=2, out_channels=3, kernel_size=(3, 5), stride=1, padding=(1, 2))

池化层：池化层主要用于缓解卷积层对位置的过度敏感性。同卷积层一样，池化层每次对输入数据的一个固定形状窗口（又称池化窗口）中的元素计算输出，池化层直接计算池化窗口内元素的最大值或者平均值，该运算也分别叫做最大池化或平均池化。
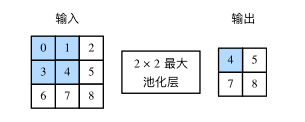
在这里插入图片描述
池化层的简单实现：

pool2d = nn.MaxPool2d(kernel_size=3, padding=1, stride=(2, 1))

二、LeNet

使用全连接层的局限性：
1.图像在同一列邻近的像素在这个向量中可能相距较远。它们构成的模式可能难以被模型识别。
2.对于大尺寸的输入图像，使用全连接层容易导致模型过大。

使用卷积层的优势：
1.卷积层保留输入形状。
2.卷积层通过滑动窗口将同一卷积核与不同位置的输入重复计算，从而避免参数尺寸过大。

LeNet分为卷积层块和全连接层块两个部分。
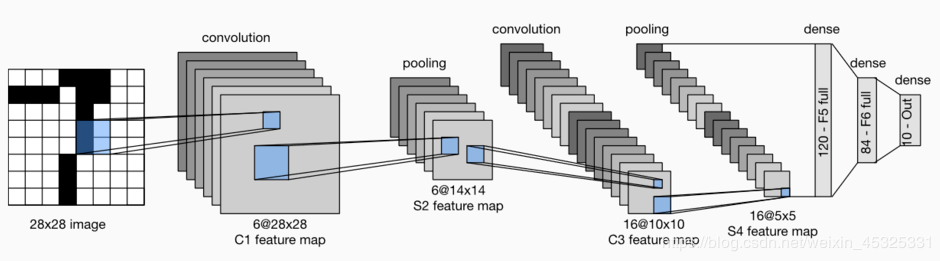
在这里插入图片描述
卷积层块里的基本单位是卷积层后接平均池化层：卷积层用来识别图像里的空间模式，如线条和物体局部，之后的平均池化层则用来降低卷积层对位置的敏感性。

卷积层块由两个这样的基本单位重复堆叠构成。在卷积层块中，每个卷积层都使用5x5的窗口，并在输出上使用sigmoid激活函数。第一个卷积层输出通道数为6，第二个卷积层输出通道数则增加到16。

全连接层块含3个全连接层。它们的输出个数分别是120、84和10，其中10为输出的类别个数。

实现过程如下：

导入包

import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
import torch
import torch.nn as nn
import torch.optim as optim
import time

网络结构

class Flatten(torch.nn.Module):  #展平操作
    def forward(self, x):
        return x.view(x.shape[0], -1)
class Reshape(torch.nn.Module): #将图像大小重定型
    def forward(self, x):
        return x.view(-1,1,28,28)      #(B x C x H x W)
net = torch.nn.Sequential(     #Lelet                                                  
    Reshape(),
    nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2), #b*1*28*28  =>b*6*28*28
    nn.Sigmoid(),                                                       
    nn.AvgPool2d(kernel_size=2, stride=2),                              #b*6*28*28  =>b*6*14*14
    nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5),           #b*6*14*14  =>b*16*10*10
    nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),                              #b*16*10*10  => b*16*5*5
    Flatten(),                                                          #b*16*5*5   => b*400
    nn.Linear(in_features=16*5*5, out_features=120),
    nn.Sigmoid(),
    nn.Linear(120, 84),
    nn.Sigmoid(),
    nn.Linear(84, 10)
)

获取数据

# 数据
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(
    batch_size=batch_size, root='/home/kesci/input/FashionMNIST2065')

计算模型net在数据集data_iter上的准确率

#计算准确率
'''
(1). net.train()
  启用 BatchNormalization 和 Dropout，将BatchNormalization和Dropout置为True
(2). net.eval()
不启用 BatchNormalization 和 Dropout，将BatchNormalization和Dropout置为False
'''
def evaluate_accuracy(data_iter, net,device=torch.device('cpu')):
    """Evaluate accuracy of a model on the given data set."""
    acc_sum,n = torch.tensor([0],dtype=torch.float32,device=device),0
    for X,y in data_iter:
        # If device is the GPU, copy the data to the GPU.
        X,y = X.to(device),y.to(device)
        net.eval()
        with torch.no_grad():
            y = y.long()
            acc_sum += torch.sum((torch.argmax(net(X), dim=1) == y))  #[[0.2 ,0.4 ,0.5 ,0.6 ,0.8] ,[ 0.1,0.2 ,0.4 ,0.3 ,0.1]] => [ 4 , 2 ]
            n += y.shape[0]
    return acc_sum.item()/n

训练

#训练函数
def train_ch5(net, train_iter, test_iter,criterion, num_epochs, batch_size, device,lr=None):
    """Train and evaluate a model with CPU or GPU."""
    print('training on', device)
    net.to(device)
    optimizer = optim.SGD(net.parameters(), lr=lr)
    for epoch in range(num_epochs):
        train_l_sum = torch.tensor([0.0],dtype=torch.float32,device=device)
        train_acc_sum = torch.tensor([0.0],dtype=torch.float32,device=device)
        n, start = 0, time.time()
        for X, y in train_iter:
            net.train()
            optimizer.zero_grad()
            X,y = X.to(device),y.to(device) 
            y_hat = net(X)
            loss = criterion(y_hat, y)
            loss.backward()
            optimizer.step()
            with torch.no_grad():
                y = y.long()
                train_l_sum += loss.float()
                train_acc_sum += (torch.sum((torch.argmax(y_hat, dim=1) == y))).float()
                n += y.shape[0]
        test_acc = evaluate_accuracy(test_iter, net,device)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f, '
              'time %.1f sec'
              % (epoch + 1, train_l_sum/n, train_acc_sum/n, test_acc,
                 time.time() - start))
# 训练
lr, num_epochs = 0.9, 10
def init_weights(m):
    if type(m) == nn.Linear or type(m) == nn.Conv2d:
        torch.nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
net = net.to(device)
criterion = nn.CrossEntropyLoss()   #交叉熵描述了两个概率分布之间的距离，交叉熵越小说明两者之间越接近
train_ch5(net, train_iter, test_iter, criterion,num_epochs, batch_size,device, lr)

测试

# test
for testdata,testlabe in test_iter:
    testdata,testlabe = testdata.to(device),testlabe.to(device)
    break
print(testdata.shape,testlabe.shape)
net.eval()
y_pre = net(testdata)

三、卷积神经网络进阶

本小节介绍了一些经典卷积神经网络及其代码实现

AlexNet

特点：
1.8层变换，其中有5层卷积和2层全连接隐藏层，以及1个全连接输出层。
2.将sigmoid激活函数改成了更加简单的ReLU激活函数。
3.用Dropout来控制全连接层的模型复杂度。
4.引入数据增强，如翻转、裁剪和颜色变化，从而进一步扩大数据集来缓解过拟合。
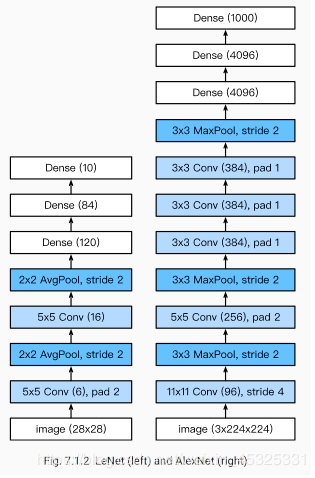
在这里插入图片描述
网络结构代码实现：

class AlexNet(nn.Module):
    def __init__(self):
        super(AlexNet, self).__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(1, 96, 11, 4), # in_channels, out_channels, kernel_size, stride, padding
            nn.ReLU(),
            nn.MaxPool2d(3, 2), # kernel_size, stride
            # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
            nn.Conv2d(96, 256, 5, 1, 2),
            nn.ReLU(),
            nn.MaxPool2d(3, 2),
            # 连续3个卷积层，且使用更小的卷积窗口。除了最后的卷积层外，进一步增大了输出通道数。
            # 前两个卷积层后不使用池化层来减小输入的高和宽
            nn.Conv2d(256, 384, 3, 1, 1),
            nn.ReLU(),
            nn.Conv2d(384, 384, 3, 1, 1),
            nn.ReLU(),
            nn.Conv2d(384, 256, 3, 1, 1),
            nn.ReLU(),
            nn.MaxPool2d(3, 2)
        )
         # 这里全连接层的输出个数比LeNet中的大数倍。使用丢弃层来缓解过拟合
        self.fc = nn.Sequential(
            nn.Linear(256*5*5, 4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            #由于使用CPU镜像，精简网络，若为GPU镜像可添加该层
            #nn.Linear(4096, 4096),
            #nn.ReLU(),
            #nn.Dropout(0.5),
            # 输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
            nn.Linear(4096, 10),
        )
    def forward(self, img):
        feature = self.conv(img)
        output = self.fc(feature.view(img.shape[0], -1))
        return output

VGGNet

VGGNet：通过重复使⽤简单的基础块来构建深度模型。
Block:数个相同的填充为1、窗口形状为3x3的卷积层,接上一个步幅为2、窗口形状为2x2的最大池化层。
卷积层保持输入的高和宽不变，而池化层则对其减半。
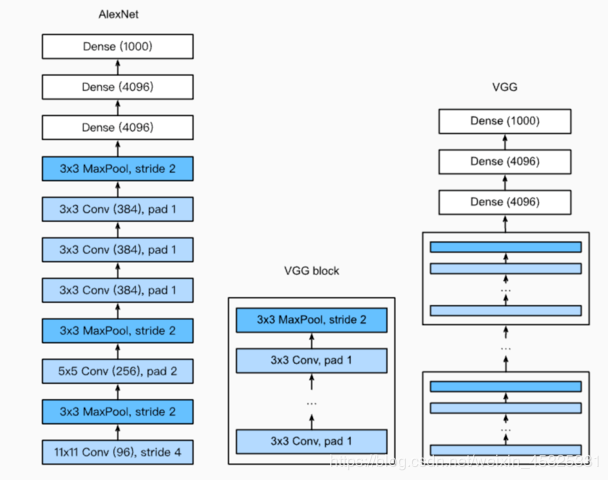
在这里插入图片描述
网络结构代码实现：

def vgg_block(num_convs, in_channels, out_channels): #卷积层个数，输入通道数，输出通道数
    blk = []
    for i in range(num_convs):
        if i == 0:
            blk.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
        else:
            blk.append(nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1))
        blk.append(nn.ReLU())
    blk.append(nn.MaxPool2d(kernel_size=2, stride=2)) # 这里会使宽高减半
    return nn.Sequential(*blk)
conv_arch = ((1, 1, 64), (1, 64, 128), (2, 128, 256), (2, 256, 512), (2, 512, 512))
# 经过5个vgg_block, 宽高会减半5次, 变成 224/32 = 7
fc_features = 512 * 7 * 7 # c * w * h
fc_hidden_units = 4096 # 任意
def vgg(conv_arch, fc_features, fc_hidden_units=4096):
    net = nn.Sequential()
    # 卷积层部分
    for i, (num_convs, in_channels, out_channels) in enumerate(conv_arch):
        # 每经过一个vgg_block都会使宽高减半
        net.add_module("vgg_block_" + str(i+1), vgg_block(num_convs, in_channels, out_channels))
    # 全连接层部分
    net.add_module("fc", nn.Sequential(d2l.FlattenLayer(),
                                 nn.Linear(fc_features, fc_hidden_units),
                                 nn.ReLU(),
                                 nn.Dropout(0.5),
                                 nn.Linear(fc_hidden_units, fc_hidden_units),
                                 nn.ReLU(),
                                 nn.Dropout(0.5),
                                 nn.Linear(fc_hidden_units, 10)
                                ))
    return net

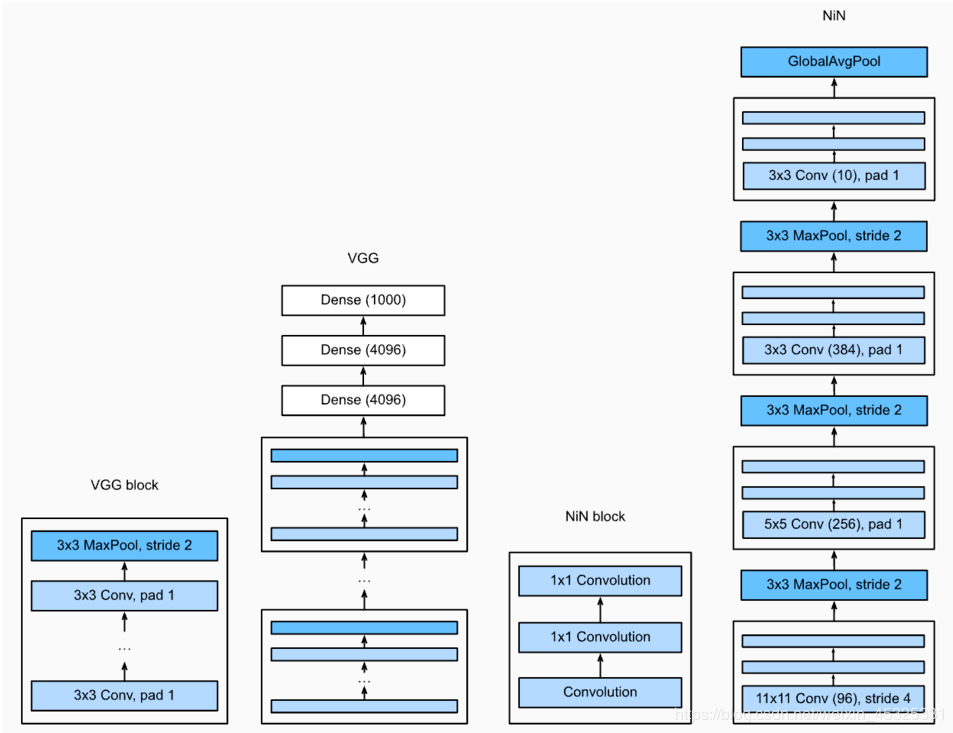
NiN

NiN：串联多个由卷积层和“全连接”层构成的小网络来构建一个深层网络。
用了输出通道数等于标签类别数的NiN块，然后使用全局平均池化层对每个通道中所有元素求平均并直接用于分类。
在这里插入图片描述
网络结构代码实现：

def nin_block(in_channels, out_channels, kernel_size, stride, padding):
    blk = nn.Sequential(nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding),
                        nn.ReLU(),
                        nn.Conv2d(out_channels, out_channels, kernel_size=1),
                        nn.ReLU(),
                        nn.Conv2d(out_channels, out_channels, kernel_size=1),
                        nn.ReLU())
    return blk
class GlobalAvgPool2d(nn.Module):
    # 全局平均池化层可通过将池化窗口形状设置成输入的高和宽实现
    def __init__(self):
        super(GlobalAvgPool2d, self).__init__()
    def forward(self, x):
        return F.avg_pool2d(x, kernel_size=x.size()[2:])
net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, stride=4, padding=0),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nin_block(96, 256, kernel_size=5, stride=1, padding=2),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nin_block(256, 384, kernel_size=3, stride=1, padding=1),
    nn.MaxPool2d(kernel_size=3, stride=2), 
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block(384, 10, kernel_size=3, stride=1, padding=1),
    GlobalAvgPool2d(), 
    # 将四维的输出转成二维的输出，其形状为(批量大小, 10)
    d2l.FlattenLayer())

GoogLeNet

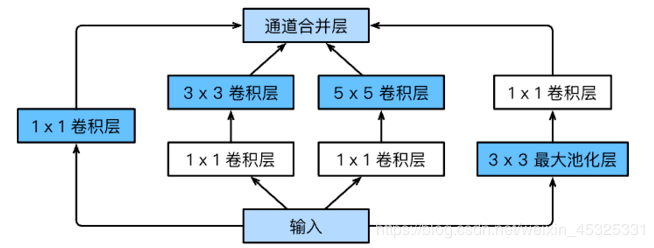
1.由Inception基础块组成。
2.inception块相当于一个有4条线路的子网络。它通过不同窗口形状的卷积层和最大池化层来并行抽取信息，并使用1×1卷积层减少通道数从而降低模型复杂度。
3.可以自定义的超参数是每个层的输出通道数，我们以此来控制模型复杂度。
在这里插入图片描述
网络结构代码实现：

class Inception(nn.Module):
    # c1 - c4为每条线路里的层的输出通道数
    def __init__(self, in_c, c1, c2, c3, c4):
        super(Inception, self).__init__()
        # 线路1，单1 x 1卷积层
        self.p1_1 = nn.Conv2d(in_c, c1, kernel_size=1)
        # 线路2，1 x 1卷积层后接3 x 3卷积层
        self.p2_1 = nn.Conv2d(in_c, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1 x 1卷积层后接5 x 5卷积层
        self.p3_1 = nn.Conv2d(in_c, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3 x 3最大池化层后接1 x 1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_c, c4, kernel_size=1)
    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        return torch.cat((p1, p2, p3, p4), dim=1)  # 在通道维上连结输出
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   d2l.GlobalAvgPool2d())
net = nn.Sequential(b1, b2, b3, b4, b5, 
                    d2l.FlattenLayer(), nn.Linear(1024, 10))

注：
本博客所有内容均参考伯禹学习平台动手学深度学习课程

作者：李明朔

动手学 pytorch

1024 个赞