电力窃漏电用户自动识别

Cindy ·

更新时间:2024-09-21

· 862 次阅读

电力窃漏电用户自动识别

参考书：《Python数据分析与挖掘实战》
工具：Pycharm2019.2.2 + Anaconda3(导入需要的库及Python.exe)
新建工程如下：
工程布局

1.背景与数据分析目的

a.通过电力系统采集到的数据，提取出窃漏电用户的关键特征，
b.构建窃漏电用户的识别模型:以实现自动检查、判断用户是否是存在窃漏电行为。

2.数据预处理

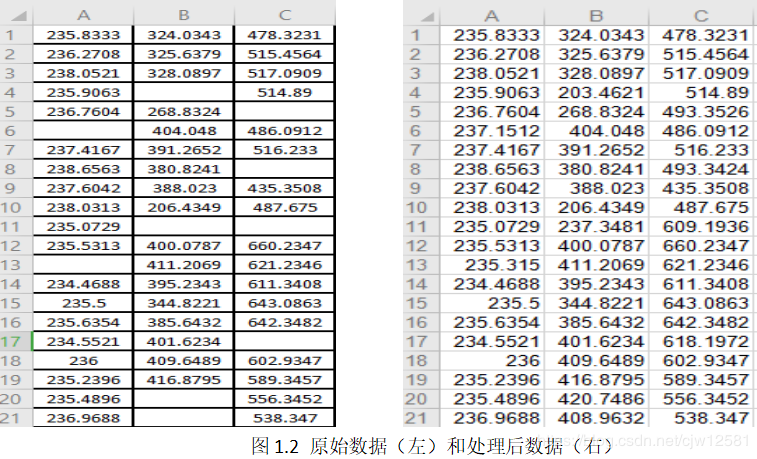
通过对拿到的数据进行数据质量分析，检查原始数据中存在的脏数据，通过查看原始数据中抽取的数据，发现存在数据缺失的现象，使用朗格拉日插值法：选取缺失值前5个数据作为前参考组，缺失值后5个数据作为后参考组，处理缺失值程序如下图1.1所示：

# -*- coding: utf-8 -*-
# 利用拉格朗日插值处理数据缺失代码
import pandas as pd  # 导入数据分析库Pandas
from scipy.interpolate import lagrange  # 导入拉格朗日插值函数
inputfile = '../data/missing_data.xls'  # 输入数据路径,需要使用Excel格式；
outputfile = '../tmp/missing_data_processed.xls'  # 输出数据路径,需要使用Excel格式
data = pd.read_excel(inputfile, header=None)  # 读入数据
# 自定义列向量插值函数
# s为列向量，n为被插值的位置，k为取前后的数据个数，默认为5
def ployinterp_column(s, n, k=5):
    y = s[list(range(n - k, n)) + list(range(n + 1, n + 1 + k))]  # 取数
    y = y[y.notnull()]  # 剔除空值
    return lagrange(y.index, list(y))(n)  # 插值并返回插值结果
# 逐个元素判断是否需要插值
for i in data.columns:
    for j in range(len(data)):
        if (data[i].isnull())[j]:  # 如果为空即插值。
            data[i][j] = ployinterp_column(data[i], j)
data.to_excel(outputfile, header=None, index=False)  # 输出结果

原始数据和数据预处理后如下图1.2所示：
图1.2 原始数据（左）和处理后数据（右）
对数据进行特征分析发现特征不明显，需要对数据进行重新构造，基于数据变换得到新的特征明显以及相关性强的专家样本数据如下图1.3所示：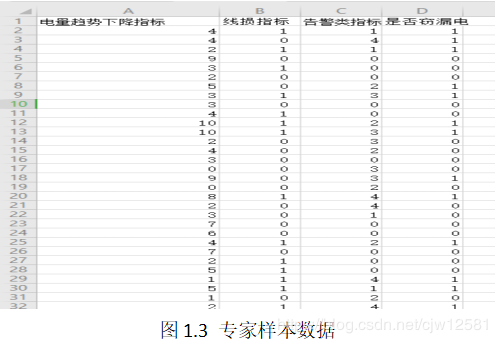

3.挖掘建模

从专家样本中随机选取20%作为测试样本，剩下的80%作为训练样本，初步选择常用的分类预测模型：CART决策树和LM神经网络。

3.1 构建CART决策树模型

程序如下图1.4所示：

# -*- coding: utf-8 -*-
# 构建并测试CART决策树模型
import pandas as pd  # 导入数据分析库
from random import shuffle  # 导入随机函数shuffle，用来打算数据
from sklearn.tree import DecisionTreeClassifier  # 导入决策树模型
from sklearn.externals import joblib
from matplotlib.pyplot import plot as plt
from sklearn.metrics import roc_curve  # 导入ROC曲线函数
datafile = '../data/model.xls'  # 数据名
data = pd.read_excel(datafile)  # 读取数据，数据的前三列是特征，第四列是标签
data = data.as_matrix()  # 将表格转换为矩阵
shuffle(data)  # 随机打乱数据
p = 0.8  # 设置训练数据比例
train = data[:int(len(data) * p), :]  # 前80%为训练集
test = data[int(len(data) * p):, :]  # 后20%为测试集
# 构建CART决策树模型
treefile = '../tmp/tree.pkl'  # 模型输出名字
tree = DecisionTreeClassifier()  # 建立决策树模型
tree.fit(train[:, :3], train[:, 3])  # 训练
joblib.dump(tree, treefile)  # 保存模型
# 混淆矩阵可视化函数
def cm_plot(y, yp):
    from sklearn.metrics import confusion_matrix  # 导入混淆矩阵函数
    cm = confusion_matrix(y, yp)  # 混淆矩阵
    import matplotlib.pyplot as plt  # 导入作图库
    plt.matshow(cm, cmap=plt.cm.Greens)  # 画混淆矩阵图，配色风格使用cm.Greens，更多风格请参考官网。
    plt.colorbar()  # 颜色标签
    for x in range(len(cm)):  # 数据标签
        for y in range(len(cm)):
            plt.annotate(cm[x, y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
    plt.ylabel('True label')  # 坐标轴标签
    plt.xlabel('Predicted label')  # 坐标轴标签
    return plt
cm_plot(train[:, 3], tree.predict(train[:, :3])).show()  # 显示混淆矩阵可视化结果
# 注意到Scikit-Learn使用predict方法直接给出预测结果。
print(tree.predict(train[:, :3]))
print(tree.predict_proba(test[:, :3])[:, 1])
fpr1, tpr1, thresholds = roc_curve(test[:, 3], tree.predict_proba(test[:, :3])[:, 1], pos_label=1)
plt.plot(fpr1, tpr1, linewidth=2, label='ROC of CART', color='green')  # 作出ROC曲线
plt.xlabel('False Positive Rate')  # 坐标轴标签
plt.ylabel('True Positive Rate')  # 坐标轴标签
plt.ylim(0, 1.05)  # 边界范围
plt.xlim(0, 1.05)  # 边界范围
plt.legend(loc=4)  # 图例
plt.show()  # 显示作图结果

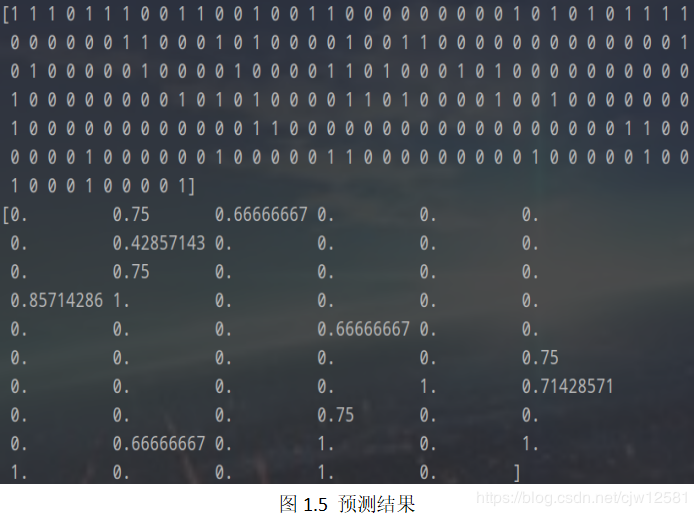
训练集和测试集的预测结果如下图1.5所示：

3.2 LM神经网络模型

程序如下图1.6所示：

# -*- coding: utf-8 -*-
import pandas as pd
from random import shuffle
from keras.models import Sequential  # 导入神经网络初始化函数
from keras.layers.core import Dense, Activation  # 导入神经网络层函数、激活函数
from sklearn.metrics import confusion_matrix  # 导入混淆矩阵函数
import matplotlib.pyplot as plt  # 导入作图库
from sklearn.metrics import roc_curve  # 导入ROC曲线函数
datafile = '../data/model.xls'
data = pd.read_excel(datafile)
data = data.as_matrix()
shuffle(data)
p = 0.8  # 设置训练数据比例
train = data[:int(len(data) * p), :]
test = data[int(len(data) * p):, :]
netfile = '../tmp/net.model'  # 构建的神经网络模型存储路径
net = Sequential()  # 建立神经网络
net.add(Dense(input_dim=3, output_dim=10))  # 添加输入层（3节点）到隐藏层（10节点）的连接
net.add(Activation('relu'))  # 隐藏层使用 relu 激活函数
net.add(Dense(input_dim=10, output_dim=1))  # 添加隐藏层（10节点）到输出层（1节点）的连接
net.add(Activation('sigmoid'))  # 输出层使用sigmoid激活函数
net.compile(loss='binary_crossentropy', optimizer='adam')  # 编译模型，使用adam方法求解##, class_mode = "binary"
net.fit(train[:, :3], train[:, 3], nb_epoch=1000, batch_size=1)  # 训练模型，循环1000次
net.save_weights(netfile)  # 保存模型C
predict_result = net.predict_classes(train[:, :3]).reshape(len(train))  # 预测结果变形
cm = confusion_matrix(train[:, 3], predict_result)  # 混淆矩阵 predict_classes是预测类别 n x 1维数组
plt.matshow(cm, cmap=plt.cm.Greens)  # 画混淆矩阵图，配色风格使用cm.Greens，更多风格请参考官网。
plt.colorbar()  # 颜色标签
for x in range(len(cm)):  # 数据标签
    for y in range(len(cm)):
        plt.annotate(cm[x, y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True label')  # 坐标轴标签
plt.xlabel('Predicted label')  # 坐标轴标签
plt.show()  # 显示作图结果
predict_result = net.predict(test[:, :3]).reshape(len(test))
fpr, tpr, thresholds = roc_curve(test[:, 3], predict_result, pos_label=1)
plt.plot(fpr, tpr, linewidth=2, label='ROC of LM')  # 作出ROC曲线
plt.xlabel('False Positive Rate')  # 坐标轴标签
plt.ylabel('True Positive Rate')  # 坐标轴标签
plt.ylim(0, 1.05)  # 边界范围
plt.xlim(0, 1.05)  # 边界范围
plt.legend(loc=4)  # 图例
plt.show()  # 显示作图结果

训练过程如图1.7所示：

3.3 CART和LM模型对比

CART和LM模型整体对比的代码如下：

# -*- coding: utf-8 -*-
import pandas as pd
from random import shuffle
from sklearn.tree import DecisionTreeClassifier  # 导入决策树模型
from sklearn.externals import joblib
datafile = '../data/model.xls'
data = pd.read_excel(datafile)
data = data.values
shuffle(data)
p = 0.8  # 设置训练数据比例
train = data[:int(len(data) * p), :]
test = data[int(len(data) * p):, :]
# 构建CART决策树模型
treefile = '../tmp/tree.pkl'  # 模型输出名字
tree = DecisionTreeClassifier()  # 建立决策树模型
tree.fit(train[:, :3], train[:, 3])  # 训练
joblib.dump(tree, treefile)  # 保存模型
# 构建LM神经网络模型
from keras.models import Sequential  # 导入神经网络初始化函数
from keras.layers.core import Dense, Activation  # 导入神经网络层函数、激活函数
netfile = '../tmp/net.model'  # 构建的神经网络模型存储路径
net = Sequential()  # 建立神经网络
net.add(Dense(input_dim=3, output_dim=10))  # 添加输入层（3节点）到隐藏层（10节点）的连接
net.add(Activation('relu'))  # 隐藏层使用relu激活函数
net.add(Dense(input_dim=10, output_dim=1))  # 添加隐藏层（10节点）到输出层（1节点）的连接
net.add(Activation('sigmoid'))  # 输出层使用sigmoid激活函数
net.compile(loss='binary_crossentropy', optimizer='adam')  # 编译模型，使用adam方法求解##, class_mode = "binary"
net.fit(train[:, :3], train[:, 3], epochs=1000, batch_size=1)  # 训练模型，循环1000次
net.save_weights(netfile)  # 保存模型
predict_result = net.predict_classes(train[:, :3]).reshape(len(train))  # 预测结果变形
# 混淆矩阵可视化函数
def cm_plot(y, yp):
    from sklearn.metrics import confusion_matrix  # 导入混淆矩阵函数
    cm = confusion_matrix(y, yp)  # 混淆矩阵
    import matplotlib.pyplot as plt  # 导入作图库
    plt.matshow(cm, cmap=plt.cm.Greens)  # 画混淆矩阵图，配色风格使用cm.Greens，更多风格请参考官网。
    plt.colorbar()  # 颜色标签
    for x in range(len(cm)):  # 数据标签
        for y in range(len(cm)):
            plt.annotate(cm[x, y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
    plt.ylabel('True label')  # 坐标轴标签
    plt.xlabel('Predicted label')  # 坐标轴标签
    return plt
cm_plot(train[:, 3], predict_result).show()  # 显示混淆矩阵可视化结果
cm_plot(train[:, 3], tree.predict(train[:, :3])).show()
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve  # 导入ROC曲线函数
predict_result = net.predict(test[:, :3]).reshape(len(test))
fpr, tpr, thresholds = roc_curve(test[:, 3], predict_result, pos_label=1)
fpr1, tpr1, thresholds = roc_curve(test[:, 3], tree.predict_proba(test[:, :3])[:, 1], pos_label=1)
plt.plot(fpr, tpr, linewidth=2, label='ROC of CART_tree', color='green')  # 作出ROC曲线
plt.plot(fpr1, tpr1, linewidth=2, label='ROC of LM')  # 作出ROC曲线
plt.xlabel('False Positive Rate')  # 坐标轴标签
plt.ylabel('True Positive Rate')  # 坐标轴标签
plt.ylim(0, 1.05)  # 边界范围
plt.xlim(0, 1.05)  # 边界范围
plt.legend(loc=4)  # 图例
plt.savefig('../tmp/ROC of CART_tree and LM.png')
plt.show()  # 显示作图结果

3.3.1混淆矩阵正确率

混淆矩阵函数代码如下：

# -*- coding: utf-8 -*-
def cm_plot(y, yp):
    from sklearn.metrics import confusion_matrix  # 导入混淆矩阵函数
    cm = confusion_matrix(y, yp)  # 混淆矩阵
    import matplotlib.pyplot as plt  # 导入作图库
    plt.matshow(cm, cmap=plt.cm.Greens)  # 画混淆矩阵图，配色风格使用cm.Greens，更多风格请参考官网。
    plt.colorbar()  # 颜色标签
    for x in range(len(cm)):  # 数据标签
        for y in range(len(cm)):
            plt.annotate(cm[x, y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
    plt.ylabel('True label')  # 坐标轴标签
    plt.xlabel('Predicted label')  # 坐标轴标签
    return plt

结果如下图1.8所示：
正确率
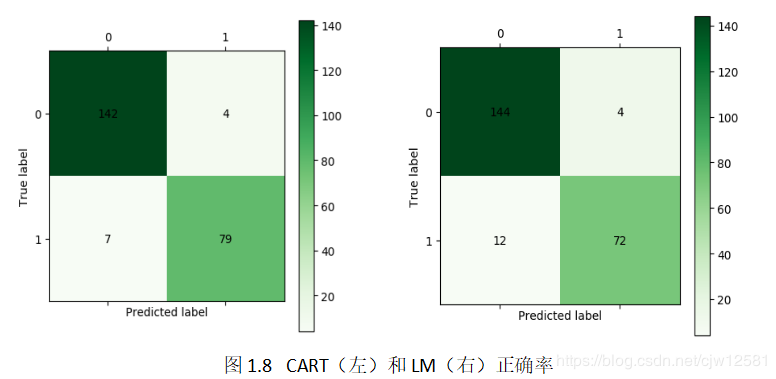
CART决策树模型与LM神经网络模型在分类准确率以及用户误判方面的对比如下表3.1所示：

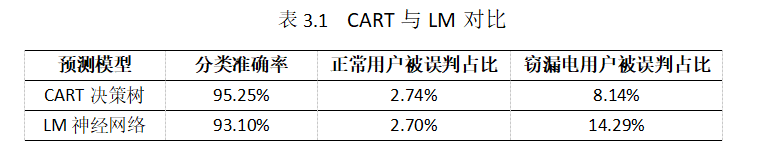
**结论：**CART模型的分类准确率略优于LM模型，但相差不大。

3.3.2 CART和LM模型的ROC曲线

比较结果如下图1.9所示：
CART和LM模型的ROC曲线
结论：LM神经网络的ROC曲线比CART决策树更加靠近单位方形的左上角且LM神经网络的ROC曲线下的面积更大，则LM神经网络预测模型的分类性能更好，更适合应用于窃漏电用户自动识别当中。
将处理后的数据作为模型输入数据，利用构建好的模型（位于工程的tmp中）计算用户的窃漏电结果，并与实际调查结果做对比，对模型进行优化，进一步提高识别准确率。