C++算法实现leetcode1252奇数值单元格数目
题目描述
整理题意
解题思路分析
具体实现
复杂度分析
代码实现
总结
题目描述题目链接:1252. 奇数值单元格的数目
给你一个 m x n 的矩阵,最开始的时候,每个单元格中的值都是 0。
另有一个二维索引数组 indices,indices[i] = [ri, ci] 指向矩阵中的某个位置,其中 ri 和 ci 分别表示指定的行和列(从 0 开始编号)。
对 indices[i] 所指向的每个位置,应同时执行下述增量操作:
ri 行上的所有单元格,加 1 。
ci 列上的所有单元格,加 1 。 给你 m、n 和 indices 。请你在执行完所有 indices 指定的增量操作后,返回矩阵中 奇数值单元格 的数目。
进阶: 你可以设计一个时间复杂度为 O(n + m + indices.length) 且仅用 O(n + m) 额外空间的算法来解决此问题吗?
提示:
1 <= m, n <= 50
1 <= indices.length <= 100
0 <= ri < m
0 <= ci < n
示例 1:
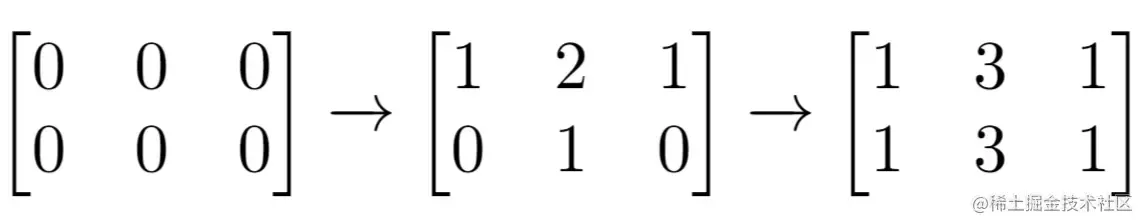
输入:m = 2, n = 3, indices = [[0,1],[1,1]]
输出:6
解释:最开始的矩阵是 [[0,0,0],[0,0,0]]。
第一次增量操作后得到 [[1,2,1],[0,1,0]]。
最后的矩阵是 [[1,3,1],[1,3,1]],里面有 6 个奇数。
示例 2:
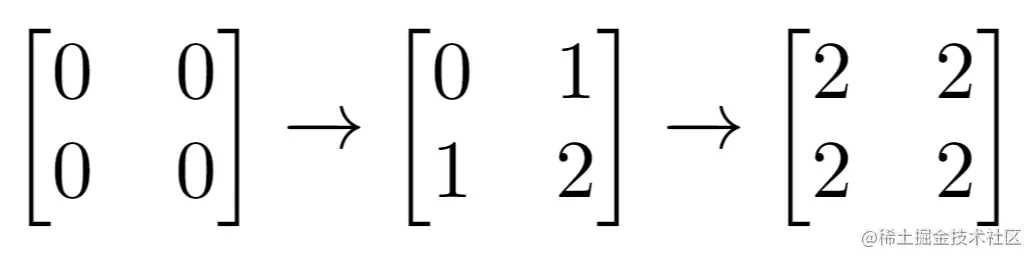
整理题意输入: m = 2, n = 2, indices = [[1,1],[0,0]]
输出: 0
解释: 最后的矩阵是 [[2,2],[2,2]],里面没有奇数。
题目给定一个 m x n 的矩阵,矩阵中每个元素最开始都为 0,然后给定一个二维数组 indices,数组中每个元素包含两个值 indices[i][0] 和 indices[i][1],分别表示对 m x n 的矩阵的第 indices[i][0] 行和第 indices[i][1] 列进行加一操作。
在执行完所有 indices 指定的增量操作后,返回矩阵中 奇数值单元格 的数目。
需要注意行和列重叠的地方是累计加的
解题思路分析观察题目数据范围较小,采用较为暴力的模拟也是可以通过的,但是我们这里按照进阶的标准来进行解题,时间复杂度为 O(n + m + indices.length) 且仅用 O(n + m) 额外空间的算法来解决此问题。
考虑到对于每一行和每一列来说,如果在 indices 中出现偶数次那么就相当于没有出现,所以我们可以统计在 indices 中行和列出现奇数的次数,这里令统计好的行和列分别记为:
出现奇数次行的总和为 sumr
出现奇数次列的总和为 sumc 那么可以通过数学计算的方式来得出最后执行完所有 indices 指定的增量操作后,返回矩阵中 奇数值单元格 的数目。
因为对于统计出来出现奇数次的行和列来说,他们相交的部分为偶数次,所以只需要减去相交部分的单元格数量即可,那么最后答案就是 sumr * n + sumc * m - sumr * sumc * 2
为什么要 * 2:是因为在 sumr * n 和 sumc * m 的时候分别加了一次相交的部分,总共就是加了两次,所以需要 * 2
具体实现在统计 indices 中进行和列出现是否为奇数次时,我们可以使用两个一维数组进行统计 sr[m] 和 sc[n],分别表示行和列出现的次数。
因为我们只需统计出现奇数次的行和列,那么我们可以采用异或 ^ 运算进行优化。
最后统计行和列出现奇数次的个数即可。
复杂度分析时间复杂度:O(n + m + indices.length),n 和 m 分别为矩阵的长和宽,indices.length 为数组 indices 的长度。
空间复杂度:O(n + m),仅需用于保存行和列的一维数组。
代码实现class Solution {
public:
int oddCells(int m, int n, vector<vector<int>>& indices) {
//统计被加上奇数次的行和列
int sr[m], sc[n];
memset(sr, 0, sizeof(sr));
memset(sc, 0, sizeof(sc));
int sumr, sumc;
sumr = sumc = 0;
for(auto &v : indices){
//如果为偶数次就是 0,奇数次为 1,用异或来变化0和1
sr[v[0]] ^= 1;
//统计奇数次的行
if(sr[v[0]]) sumr++;
else sumr--;
sc[v[1]] ^= 1;
//统计奇数次的列
if(sc[v[1]]) sumc++;
else sumc--;
}
//奇数次行个数加上奇数次列个数,减去相交为偶数次的点,因为加了两遍所以要 *2
int ans = sumr * n + sumc * m - sumr * sumc * 2;
return ans;
}
};
总结
该题难点在于如何优化时间复杂度为 O(n + m + indices.length) 且仅用 O(n + m) 额外空间的算法来解决此问题。
通过统计行和列出现的次数便能进一步实现优化。核心思想在于计数。
测试结果:

以上就是C++实现leetcode 1252奇数值单元格的数目题解的详细内容,更多关于C++奇数值单元格的数目的资料请关注软件开发网其它相关文章!