Google OR-Tools(四) 约束编程 Constraint Programming
本文参考Google OR-Tools官网文档介绍OR-Tools的使用方法。
1 约束满足问题 1.1 CSP定义在前一篇文章中我提到Google OR-Tools中解决整数规划问题有MP Solver和CP Solver两种工具,但是只介绍了MP Solver,而这篇文章则会介绍CP Solver。之所以会有这两种工具,是因为虽然都是解决整数规划,各自面对的问题类型还是有区别的,CP Solver一般用于约束满足问题(Constraint Satisfaction Problem),简称CSP。
一个约束满足问题包括有限变量集、每个变量的有限论域和有限约束集,每条约束限制了变量集赋值的组合,约束满足问题的解是为每个变量赋一个对应论域上的值,使之满足所有的约束。一般情况,解约束满足问题的目标是只要找到一个解就行,不过也可能要找出所有可行解中最优的那个。
举个简单的例子,比如一个人需要穿鞋、衬衫和裤子,其中每样东西都有一定的选择:鞋有运动鞋、皮鞋两双;衬衫有红色和白色两件;裤子有蓝色、灰色和牛仔裤三条。但是必须符合如下的规则:
运动鞋配牛仔裤; 皮鞋只能与灰裤子和白衬衫搭配; 白衬衫可以和牛仔裤或者蓝裤子搭配; 红衬衫只能与灰裤子搭配;这个穿衣规则就是问题的约束,问题变量集合为{鞋,裤子,衬衫},而每种物品可选择的样式就构成了变量的论域。
下面是CSP问题的数学定义:
用一个三元组(V,D,C)(V,D,C)(V,D,C)来表示CSP,其中
对于一个CSP(V,D,C)CSP(V,D,C)CSP(V,D,C):
如果一个CSP(V,D,C)CSP(V,D,C)CSP(V,D,C)是kkk-可满足的,当且仅当VVV中所有由kkk个变量组成的子集都存在一组标识使得这组标识满足所有和它们相关的约束 一个有nnn个变量的CSP是可满足的,如果它是nnn-可满足的所以根据定义,如果一个CSP是可满足的,那么它至少存在一个解;如果一个CSP是不可满足的,则问题的解不存在。
乍看这个CSP的定义,会感觉很难和非线性规划的一般方程形式相关联,这个其实就是CSP问题和通常的整数规划问题的区别,还是那上面那个穿衣服的案例来分析,这个例子完全是用自然语言表示的各种逻辑关系构成的,没有人数、长度这类很显然的变量存在,所以这种问题很难直接用一般的非线性规划方程表达出来。当然只要变量定义得合适还是可以写成一般的非线性规划形式的,例如我们如果给每个衣物关联一个布尔变量,表示是否穿这个衣物,那么各种约束就变成了这些布尔变量的逻辑关系了。以我个人的理解看,CSP和一般的整数规划相比,主要是以下这些特点:
问题由很多带逻辑关系的约束构成 变量通常会是布尔变量 很难用线性表达式写成一般的方程形式 很多时候约束带有If-Than的条件信息在现实中,很多问题(通常也会称为组合优化问题)都属于CSP,例如生产调度、物流规划、路由选择、资源分配等等,解空间规模一般比较大,而且需要符合很多现实规则约束,因此其求解难度一般都很大。
1.2 CSP相关算法针对CSP的算法主要分成了两类,一类属于非完备性算法,另一类属于完备性算法。非完备性算法包括各种启发式或元启发式算法,例如模拟退火、遗传算法,它们的目的不在于找到精确的最优解,只要在合理的时间找到一个相对最优解,这些算法不会遍历整个解空间,因此如果原问题有解,那么通常非完备性算法可以快速找到一个合理的解,但是如果原问题无解,非完备性算法无法证明无解,换句话说即使跑了很长时间算法得到的解不合理,我们也不能认定该问题无解;而完备性算法则以各种搜索和推理技术为主,称其为完备是因为这些算法实际上是搜索了整个解空间的,因此如果这些算法得出的结论是无解,那么该问题就是无解的,同时如果问题有解,得到的最终解也肯定是最优的。从我个人的使用经验来猜测,CP Solver内部应该是采用的完备性算法,使用CP Solver求解CSP,如果约束有冲突,问题实际是无解的,CP Solver会第一时间判断出来。关于完备性算法,我参阅了一点资料,以下是我个人的一些理解。
目前通常的完备性CSP算法是将以回溯为主的搜索技术与以约束传播为主的推理技术相结合,通过搜索技术确保解空间被完整遍历,同时结合推理技术动态地省去冗余的子空间,从而加快求解速度。基础的回溯就类似于深度优先遍历,按照一定的次序依次实例化变量,如果进行到某一个变量时发现该变量的论域内没有任何值可以满足约束,则直接回退到上一个变量,取下一个值进行实例化。例如XXX和YYY是实例化次序相邻的两个变量,它们的论域都是{1,2,3}\{1,2,3\}{1,2,3},并且需要满足约束X+Y=1X+Y=1X+Y=1,假设XXX实例化为了1,然后轮到YYY实例化,结果发现YYY取任何值都无法满足约束,则停止XXX实例化为1的分支,回退到XXX,开始XXX实例化为2的分支。

回溯可以实现部分的剪枝效果,但是存在大量冗余的实例化操作,比如这个例子里,显然问题是无解的,把XXX的论域都实例化一遍是没有意义的。针对这个问题,需要引入约束传播算法,就是在求解过程中使用约束信息删除变量中一些不参与解的值从而减小搜索空间。约束传播算法以相容性技术为主,而弧相容则是相容性技术最基础的概念。
对于一个二元CSP的约束图中的某一个弧(Xi,Xj)(X_i, X_j)(Xi,Xj),称它是弧相容的(Arc Consistency, AC),当且仅当对于XiX_iXi论域中能满足XiX_iXi上一元约束的每一个值aaa,都在XjX_jXj的论域中存在一个值bbb,使得bbb满足XjX_jXj上一元约束,并且(a,b)(a,b)(a,b)满足XiX_iXi和XjX_jXj上的二元约束C(Xi,Xj)C(X_i,X_j)C(Xi,Xj) 一个CSP是弧相容的,当且仅当它的约束图中每一条弧都是弧相容的 对于问题P在进行弧相容检查时,如果得到某一变量的论域为空,则此问题无解我们还是用上面那个例子,不过把约束改成X+Y=3X+Y=3X+Y=3,然后对XXX和YYY进行相容性检查,变量XXX中值 3 在变量YYY中没有值,能够满足约束X+Y=3X+Y=3X+Y=3,因此被移走,同理变量YYY中值 3 也被移走,最后论域得到了缩减:

再把约束改回X+Y=1X+Y=1X+Y=1进行相容性检查,则YYY的论域将为空,则该问题无解,可以直接退出计算了。所以通过约束传播,一方面可以迅速判断是否有解,另一方面可以大大缩小每一次搜索的解空间,从而达到加快计算的效果。
从上面对搜索和推理算法的简单介绍可以看到完备性算法的优点在于可以第一时间检查问题是否有解,并且一定能给出最优解,但缺点也很明显,虽然采用了各种减小搜索空间的技术,当问题的规模增大时,搜索空间仍然以指数级增长,这些技术对计算效率的提升也越来越小。
1.3 约束编程按照定义,约束编程(Constraint Programming, CP)是围绕关系约束这一数学概念建立起来的方法论,是研究基于约束的组合优化问题的计算系统。实际生活中有很多复杂的组合优化问题,我们当然可以对不同的问题以合适的算法分别设计和开发计算系统,但是这样不具有通用性。约束编程或者说约束程序设计就是以高效的约束求解技术为核心,结合强说明性的问题描述方式建立的组合优化计算系统,对于使用者来说,可以用约束编程语言表达问题的任意约束,并且考虑新类型的约束时(特别是在面向对象框架中),只需要对约束系统进行扩展。像Google OR-Tools的CP Solver就是一个CP系统,不仅内部提供了高效的求解CSP问题的算法,外部也提供了灵活的约束语言接口,用于构建适合自身项目的优化问题模型。
2 OR-Tools Demo 2.1 N皇后问题N皇后问题可以描述为,是否可以在一个N X N的棋盘上放置N个皇后,使得它们之间互相不会攻击,所谓攻击指的是棋盘上同一行、同一列和同一对角线上不会有两个皇后。例如下面这张图就是4皇后的一个可行方案
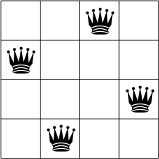
N皇后问题是一个典型的CSP问题,我们并不需要找到一个最优解,而是要找到满足约束的解。
我们来分析下如何对这个问题进行建模。首先需要确定决策变量是什么,对于CSP问题,确定决策变量是相当重要也是最具难度的步骤之一,好的决策变量可以方便约束的构建,反之不合适的决策变量会加大建立约束的难度,甚至影响计算的效率。对于N皇后问题,我们的一种方案是每个点位分配一个布尔变量Q(i,j)Q(i,j)Q(i,j),如果这个变量为True,表示第i行第j列放置了一个皇后。但这种方式并不是太好,对于N X N的棋盘,将会有N X N 个变量,无疑会加大搜索空间。另一种更好的方案是定义一个一维数组Q[j]=i,i,j=0,1,...,NQ[j]=i,i,j=0,1,...,NQ[j]=i,i,j=0,1,...,N,表示第j列上的皇后在第i行,这样首先变量的数量只有N个,然后在变量阶段就已经隐含了一个约束:必须要有N个皇后被放置。
然后我们利用决策变量Q[j]Q[j]Q[j]来定义约束:
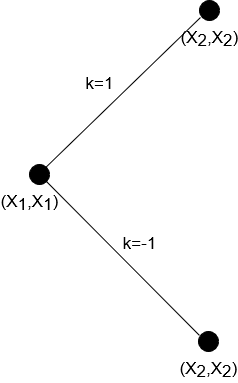
因此我们只需要保证所有Q[j]Q[j]Q[j]对应的两个数组Q[j]+jQ[j]+jQ[j]+j和Q[j]−jQ[j]-jQ[j]−j的值都不相同 2.2 代码
新建一个.Net Core应用,下载OR-Tools。在程序开头引用Google.OrTools.Sat库
using Google.OrTools.Sat;
首先我们定义一个CpModel对象。不同于之前线性规划,CP系统将模型model和求解器Solver在接口层分开了,这也符合CP系统的方法论。
//Create CP Model
var model = new CpModel();
然后定义决策变量数组
//Create Variables
List queens = new List();
for(int j=0;j<N;j++)
{
queens.Add(model.NewIntVar(0, N - 1, $"queen_{j}"));
}
接着定义约束一,不允许两个及以上的皇后出现在同一行。OR-Tools直接提供了AddAllDifferent接口实现一个数组元素互不相同的约束
//All queens are in different rows
model.AddAllDifferent(queens);
约束二,对角线上不允许两个及以上的皇后
//No two queens can be on the same diagonal.
List diag1 = new List();
List diag2 = new List();
for (int j = 0; j < N; j++)
{
var q1 = model.NewIntVar(0, 2 * N, $"diag1");
diag1.Add(q1);
model.Add(q1 == queens[j] + j);
var q2 = model.NewIntVar(-N, N, $"diag2");
diag2.Add(q2);
model.Add(q2 == queens[j] - j);
}
model.AddAllDifferent(diag1);
model.AddAllDifferent(diag2);
然后就可以定义Solver了
//Create Solver
var solver = new CpSolver();
但是在调用计算之前,我们可以先定义一个回调接口供Solver使用,方便获取所有的解
public class QueenSolutionCallback:CpSolverSolutionCallback
{
private int solutionCount=0;
private List queens;
public QueenSolutionCallback(List queens)
{
this.queens = queens;
}
public override void OnSolutionCallback()
{
Console.WriteLine($"#Solution {solutionCount}:");
for(int row=0;row<queens.Count;row++)
{
string s = "";
for(int column=0; column < queens.Count;column++)
{
if(Value(queens[column])==row)
{
s += "Q ";
}
else
{
s += "_ ";
}
}
Console.WriteLine(s);
}
Console.WriteLine();
solutionCount++;
}
}
最后计算结果
//Get the result
QueenSolutionCallback cb = new QueenSolutionCallback(queens);
var status = solver.SearchAllSolutions(model, cb);
我们看一下4皇后问题的结果:

4个皇后时有2个解。再看下8皇后的情况:

这时将有92个解。
完整的程序
using System;
using System.Collections.Generic;
using Google.OrTools.Sat;
namespace Demo4
{
class Program
{
static void Main(string[] args)
{
Nqueen(8);
}
static void Nqueen(int N)
{
//Create CP Model
var model = new CpModel();
//Create Variables
List queens = new List();
for(int j=0;j<N;j++)
{
queens.Add(model.NewIntVar(0, N - 1, $"queen_{j}"));
}
//All queens are in different rows
model.AddAllDifferent(queens);
//No two queens can be on the same diagonal.
List diag1 = new List();
List diag2 = new List();
for (int j = 0; j < N; j++)
{
var q1 = model.NewIntVar(0, 2 * N, $"diag1");
diag1.Add(q1);
model.Add(q1 == queens[j] + j);
var q2 = model.NewIntVar(-N, N, $"diag2");
diag2.Add(q2);
model.Add(q2 == queens[j] - j);
}
model.AddAllDifferent(diag1);
model.AddAllDifferent(diag2);
//Create Solver
var solver = new CpSolver();
//Get the result
QueenSolutionCallback cb = new QueenSolutionCallback(queens);
var status = solver.SearchAllSolutions(model, cb);
Console.WriteLine(status);
}
public class QueenSolutionCallback:CpSolverSolutionCallback
{
private int solutionCount=0;
private List queens;
public QueenSolutionCallback(List queens)
{
this.queens = queens;
}
public override void OnSolutionCallback()
{
Console.WriteLine($"#Solution {solutionCount}:");
for(int row=0;row<queens.Count;row++)
{
string s = "";
for(int column=0; column < queens.Count;column++)
{
if(Value(queens[column])==row)
{
s += "Q ";
}
else
{
s += "_ ";
}
}
Console.WriteLine(s);
}
Console.WriteLine();
solutionCount++;
}
}
}
}
作者:皇家园林巡游者