【线代笔记】1.1 Vectors and Combinations - 向量与线性组合
在数学中,向量即为带有大小和方向的量。在线性代数中经由抽象化,得到更一般的向量概念。
可以将向量定义为向量空间的元素,只需满足以下向量的加法和向量的乘法两个规则即可
将单独的数字进行组合变为一个向量,通常情况下用列向量表示。
v=[v1v2]
\mathbf{v}=\begin{bmatrix}v_1\\ v_2\end{bmatrix}
v=[v1v2]
Vector Addition - 向量的加法
v=[v1v2]andw=[w1w2]add tov+w=[v1+w1v2+w2] \mathbf{v}=\begin{bmatrix} v_1\\ v_2 \end{bmatrix} \quad and \quad \mathbf{w}=\begin{bmatrix} w_1\\ w_2 \end{bmatrix} \quad add \ to \quad \mathbf{v+w}=\begin{bmatrix} v_1+w_1\\ v_2+w_2 \end{bmatrix} v=[v1v2]andw=[w1w2]add tov+w=[v1+w1v2+w2]
Scalar Multiplication - 向量的乘法
2v=[2v12v2]=v+v−v=[−v1−v2] 2\mathbf{v}=\begin{bmatrix} 2v_1 \\ 2v_2 \end{bmatrix} =\mathbf{v} + \mathbf{v} \quad -\mathbf{v}=\begin{bmatrix} -v_1 \\ -v_2 \end{bmatrix} 2v=[2v12v2]=v+v−v=[−v1−v2]
-v和v两个向量相加的结果为0,和数字0的概念是不一样的
Linear Combinations - 线性组合将上述的两个法则合起来就得到了线性组合的概念
cv+dw
c \mathbf{v} + d \mathbf{w}
cv+dw
若我们将线性组合用可视化,可理解为从原点(0,0)出发的矢量
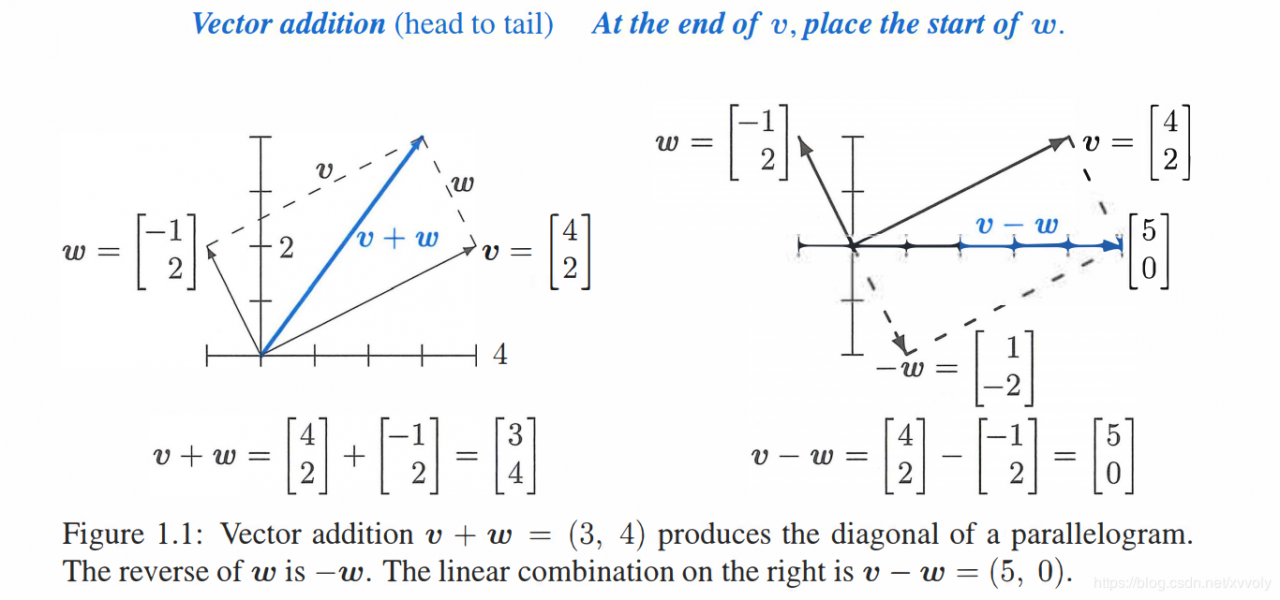
上面我们的列向量包含了两个分量,对应于xy平面上的一个点
当分量从2个变为3个的时候,对应于xyz空间中的一个点
除了上面的列向量表示方法外,也可以用(v1,v2,v3)(v_1,v_2,v_3)(v1,v2,v3)来表示一个含有三个分量的向量
The Important Questions - 重要的问题假设有三维空间中的非零向量 u, v, w
What is the picture of all combinations cu ? => The combinations cu fill a line through (0, 0, 0)
What is the picture of all combinations cu + dv ? => The combinations cu+ dv fill a plane through (0, 0, 0)
What is the picture of all combinations cu + dv + ew ? => The combinations cu+ dv + ew fill three-dimensional space
u、v不共线,w不在u、v构成的平面 => Line, then plane, then space
总结:本节介绍了线性组合的含义、表示和一些基本的问题
作者:沉默的溪