Codeforces 1341 D. Nastya and Scoreboard（dp）

Bree ·

更新时间:2024-11-14

· 692 次阅读

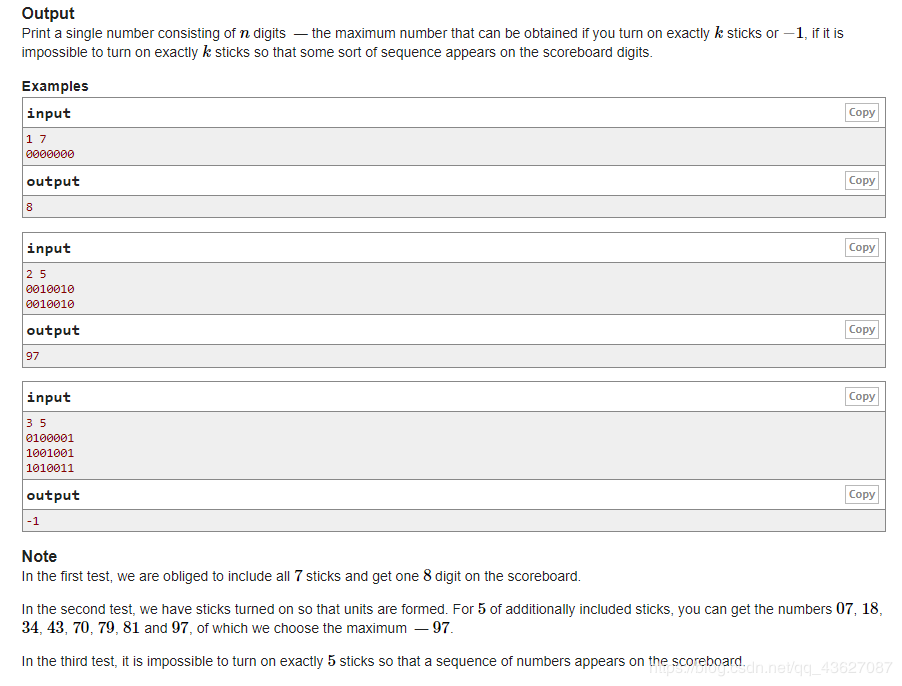
在这里插入图片描述

题意：

一个 nnn 个数字的计数器，每一个数字都是由七个灯管组成，现在给出每个数组的初始显示情况，问再点亮 kkk 个灯管的话能显示的最大的数是多少，如果不能构成一串数字，就输出 −1-1−1。
预处理 0 90~90 9 对应数码位字符串状态成整数，dpdpdp 从最后一位数码位往前构造到第 iii 位数字时点亮 jjj 根灯管能否构造出数字，1−n1-n1−n 第 iii 个数码位可以构造出数字的话就算出要点亮几根灯管。

AC代码：

const int N = 2010;
int dp[N][N];
int n, m;
int res, tmp, cnt,pos;
bool flag, ok;
string s[N];
string num[10] = {"1110111", "0010010", "1011101", "1011011", "0111010", "1101011", "1101111", "1010010", "1111111", "1111011"};
vector ans;
int cal(int i, int k)//计算需要几根灯管
{
	int sum = 0;
	rep(j, 0, 6)
	{
		if (s[i][j] > num[k][j])
			return -1;//不能熄灭，只能点亮
		else
			sum += num[k][j] - s[i][j];
	}
	return sum;
}
int main()
{
	sdd(n, m);
	rep(i, 1, n)
		cin >> s[i];
	mem(dp, 0);
	dp[n + 1][0] = 1;
	pos = 0;
	per(i, n, 1)
	{
		per(j, pos, 0)
		{
			if (!dp[i + 1][j])
				continue;
			rep(k, 0, 9)
			{
				int x = cal(i, k);//变到k这个数字需要点亮几根灯管
				if (x >= 0)
					dp[i][j + x] |= dp[i + 1][j];//点亮j+x可以构成数字
				pos = max(pos, j + x);
			}
		}
	}
	flag = 0;
	rep(i, 1, n)
	{
		ok = 0;
		per(j, 9, 0)
		{
			tmp = cal(i, j);
			if (tmp  m || !dp[i + 1][m - tmp])
				continue;
			else
			{
				m -= tmp;
				ans.pb(j);
				ok = 1;
				break;
			}
		}
		if (!ok)
			flag = 1;
	}
	if (!flag)
	{
		for (auto it : ans)
			printf("%d", it);
		puts("\n");
	}
	else
		puts("-1");
	return 0;
}

作者：邵光亮

dp CodeForces AND

1024 个赞