CodeForces1230 F. Konrad and Company Evaluation (复杂度分析)
题意:
作者:是我菜了
有n个人m个敌对关系,
一开始第x个人的工资是x
有q次操作,每次操作会给一个人的编号x
然后将x的工资变为所有人中最多的。
如果a和b是敌对关系,a的工资比b高,那么a会嘲讽
如果a嘲讽b,b嘲讽c,那么(a,b,c)是一个三元组
问每次操作之后一共有多少对三元组
数据范围:n,m<=1e5,q<=1e5
三元组图例(未修改工资时):
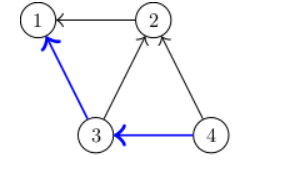
图中三元组一共4组:
4->3->1
4->3->2
4->2->1
3->2->1
建立有向边,记录入度和出度
枚举三元组的中间点,那么每个点的贡献=入度x出度
显然每次修改就是把一些边翻转
主要难点在于如何在修改的时候维护答案并保证算法复杂度,没想到暴力修改就行了。
感觉复杂度分析有点玄学
大概意思似乎是m有向边,入度和出度都只有m,先假设点权大的指向点权小的,显然入度大于√m的不超过√m个,
1.对于入度大于√m的,就算每次操作都是O(n),把这些点全部修改了也只有n√m,
且每个点每次修改只给相连的点增加1的入度,这√m个点全部修改也只让相连的点增加√m
假设全部修改,那么剩下似乎就只是处理入度小于√m的了:
2.对于入度小于√m的,单次修改是√m的,q次也只有q√m
那么如果视n、m、q同阶,那么总复杂度也只有n√n
不知道这样推对不对
code:#include
using namespace std;
#define int long long
const int maxm=1e5+5;
vectorg[maxm];//g[i]存比i大的
int in[maxm],out[maxm];
int n,m;
signed main(){
ios::sync_with_stdio(0);cin.tie(0);
cin>>n>>m;
for(int i=1;i>a>>b;
if(a>b)swap(a,b);
g[a].push_back(b);
out[a]++,in[b]++;//因为vector是小的存大的,因此我边也是小的指向大的,方向的选择不影响答案
}
int sum=0;
for(int i=1;i<=n;i++){
sum+=in[i]*out[i];
}
cout<<sum<>q;
while(q--){
int x;cin>>x;
sum-=in[x]*out[x];
for(int v:g[x]){
g[v].push_back(x);
sum-=in[v]*out[v];
in[v]--,out[v]++;
out[x]--,in[x]++;
sum+=in[v]*out[v];
}
sum+=in[x]*out[x];
g[x].clear();
cout<<sum<<endl;
}
return 0;
}
作者:是我菜了
相关文章
Karima
2020-09-06
Serepta
2021-06-02
Kiran
2021-02-22
May
2022-07-15
Penelope
2022-07-15
Querida
2022-07-17
Kande
2022-09-09
Welcome
2022-09-29
Lassie
2022-09-29
Karima
2022-10-15
Bonnie
2022-10-23
Laura
2022-10-23
Xylona
2022-10-24
Tertia
2022-10-24
Keelia
2022-10-24
Honey
2022-10-24
Gabriela
2022-10-24
Bertha
2022-11-04