论文笔记：Cluster Alignment with a Teacher for Unsupervised Domain Adaptation

        最近因为个人需要看了一些 DADADA 和 DRDRDR 的文章。
        这篇文章比较有意思的是：将聚类设计成目标函数，从而一方面实现经网络抽取特征在分布上的自然聚类，一方面因为特征分布的聚类自然提高了分类效果，一方面加快了聚类的速度，同时最主要的就是实现了不同源域之间的结构的细粒度对齐，从而促进 UDAUDAUDA 算法的性能。

        DADADA 有一个基本的解决思路就是：认为源域 SSS 与目标域 TTT 的边缘分布在高层语义空间是可以等价的，因此，致力于在高层隐空间拉近两个域的分布，设计为一个类似 min⁡θLd(XS,XT)=D(f(XS;θ),f(XT;θ))\min_{\theta} \mathcal L_d(\mathcal X_S,\mathcal X_T)=\mathcal D(f(\mathcal X_S;\theta), f(\mathcal X_T;\theta))minθ​Ld​(XS​,XT​)=D(f(XS​;θ),f(XT​;θ)) 的目标函数。作者 argue 说这只是宏观的拉近（Global），对于如下图的两种情形会可能导致两个隐分布错误对齐：

        以分类任务为例，图中两个域都含有相同的两种类别，但左图中类别的形状（分布）不同；右图中则是相同类别的规模（数量）不同。换句话说，当两个域之间相同类别在数据特征上存在明显的差异如分布和数量，全局的 alignmentalignmentalignment 约束下可能会导致对齐错误。
        在本文中，作者考虑了域内部的 class-conditioal fine-level structure，并且通过使用簇中心（即均值）的拉近来避免了需要对数量和形状的考虑。

        分类任务，源域有 label 标注，目标域无 label 标注，但可以使用 伪标签 （Pseudo Labels）。
        目标函数是有监督的分类 losslossloss:
min⁡θLy(XS,YS)=1N∑i=1Nl(h(xSi;θ),ySi)(1)\min_{\theta}\mathcal L_y(\mathcal X_S,\mathcal Y_S)={1\over{N}}\sum_{i=1}^N \mathcal l(h(x_S^i;\theta),y_S^i)\tag{1}θmin​Ly​(XS​,YS​)=N1​i=1∑N​l(h(xSi​;θ),ySi​)(1)        其中，下标 SSS 表示源域数据；xSix_S^ixSi​ 是待识别的图像；ySiy_S^iySi​ 是对应的标签；h=g∘fh=g \circ fh=g∘f，fff 是特征抽取器，ggg 是分类器；NNN 是源域的大小；lll是目标函数，可以是交叉熵等。

        为了使模型在源域训练能够很好泛化到目标域，我们希望不管是源域的图像还是目标域的图像，其经过 fff 得到的特征分布要尽可能地相似，即特征集合 F(XS;f)\mathcal F(\mathcal X_S;f)F(XS​;f) 和 F(XT;f)\mathcal F(\mathcal X_T;f)F(XT​;f) 尽可能一致。
        但我们知道，不同域之前由于收集过程的不同必然存在差别，即我们所说的 domain shift。但我们可以对它们进行对齐。
        作者说以前的 DADADA 只是宏观地进行这个特征集合的散度对齐，这是不充分的，还需要考虑域内部不同类的特点即 class-conditional fine-level structure。
        并且我们不希望说是在训练完成后，每次输入目标域图像测试的时候，都要通过聚类或者最近邻等的方法进行特征匹配，而是希望模型的 fff 本身就可以抽取出图像的 domain invariant features。
        因此我们可以对 {f(xSi)}\{f(x_S^i)\}{f(xSi​)} 和 {f(xTi)}\{f(x_T^i)\}{f(xTi​)} 做正则化，作为目标函数的一部分，一同参与训练。
        为了实现细粒度的对齐，那么我们需要：首先是聚类，其次是对应相同类别的簇作对齐。

        首先是聚类！
        1）要确定聚多少类？很明显，有 KKK 个类就聚 KKK 类；
        2）根据什么聚类？即一个距离评价指标 ddd，如特征之间欧几里得距离等；
        3）目标：在每个域间，同类特征相近，异类特征相疏；
        综上，我们可以构造下面的目标函数：
Lc(XS,XT)=Lc(XS)+L(XT)(2)\mathcal L_c(\mathcal X_S,\mathcal X_T)=\mathcal L_c(\mathcal X_S)+\mathcal L(\mathcal X_T)\tag{2}Lc​(XS​,XT​)=Lc​(XS​)+L(XT​)(2)         其中，有：
Lc(X)=1∣X∣2∑i=1∣X∣∑j=1∣X∣[δijd(f(xi),f(xj))+(1−δij)max⁡(0,m−d(f(xi),f(xj)))](3)\mathcal L_c(\mathcal X)={1\over{|\mathcal X|^2}}\sum_{i=1}^{|\mathcal X|}\sum_{j=1}^{|\mathcal X|}[\delta_{ij}d(f(x^i),f(x^j))+(1-\delta_{ij})\max(0,m-d(f(x^i),f(x^j)))]\tag{3}Lc​(X)=∣X∣21​i=1∑∣X∣​j=1∑∣X∣​[δij​d(f(xi),f(xj))+(1−δij​)max(0,m−d(f(xi),f(xj)))](3)
        其中，
δij={1yi=yj0otherwise.(4)\delta_{ij}= \begin{cases} 1& y^i=y^j\\ 0& otherwise. \end{cases}\tag{4} δij​={10​yi=yjotherwise.​(4)        公式 (5)(5)(5) 实际上是说，假如两个实例的属于同一类，则第二项为 0，最小化第一项；假如属于不同类，则第一项为 0，第二项表示只有当两个实例的特征超过阈值 mmm 的时候，才不计算 losslossloss，如果小于 mmm，那还需要继续拉大，因为此时最小化 m−d(f(xi),f(xj))m-d(f(x^i),f(x^j))m−d(f(xi),f(xj)) 就是在最大化 d(f(xi),f(xj))d(f(x^i),f(x^j))d(f(xi),f(xj)) 逼近于 mmm。
        那现在的问题就是，目标域的数据没有标签，怎么办？答案是使用 伪标签，这就引入了一个 teacher 来对目标域的图像产生伪标签，从而我们可以计算 δij\delta_{ij}δij​。

那很明显，假如产生的伪标签不准确，那么这个 losslossloss 就会产生副作用，促进了源域的类别结构与目标域的类别结构之间的错误对齐。
作者在本文中是这么说的：首先由于源域与目标域之间有较大相似性，因此伪标签可以对大部分目标域的图像是正确的（尽管 the highest probability 不会很高）；其次是 teacher 是通过多个其他的样本作出的判断，可以减轻这个负面的影响。

        在上面公式 (2)(2)(2) 的约束下，fff 提取的特征有这样一个趋势：同类别的图像的特征很相近，异类别的图像的特征则相差更大。因此本身这就有利于提高分类器的准确度。
        其次，我们可以认为，fff 提取的特征已经被聚好类了。
        下一步我们要做的就是对齐。
        即：
min⁡θD(FS,k,FT,k)(5)\min_{\theta}\mathcal D(\mathcal F_{S,k},\mathcal F_{T,k})\tag{5}θmin​D(FS,k​,FT,k​)(5)         即两个域之间，相同类别的图像特征要对齐。
        受启发于 GANGANGAN 训练技巧中的 Feature MatchingFeature~MatchingFeature Matching，作者提出了 conditional 版本的特征匹配 loss，即
La(XS,XT)=1K∑k=1K∣∣λS,k−λT,k∣∣22(6)\mathcal L_a(\mathcal X_S,\mathcal X_T)={1\over{K}}\sum_{k=1}^K ||\lambda_{S,k}-\lambda_{T,k}||_2^2 \tag 6La​(XS​,XT​)=K1​k=1∑K​∣∣λS,k​−λT,k​∣∣22​(6)         其中，
λS,k=1∣XS∣∑xSi∈XS,kf(xSi), λT,k=1∣XT∣∑xTi∈XT,kf(xTi)(7)\lambda_{S,k}={1\over{|\mathcal X_S|}}\sum_{x_S^i\in\mathcal X_{S,k}}f(x_S^i),~\lambda_{T,k}={1\over{|\mathcal X_T|}}\sum_{x_T^i\in\mathcal X_{T,k}}f(x_T^i) \tag 7λS,k​=∣XS​∣1​xSi​∈XS,k​∑​f(xSi​), λT,k​=∣XT​∣1​xTi​∈XT,k​∑​f(xTi​)(7)         使用均值进行度量的好处是：可以避免形状和数量带来的不平衡。

        最后作者还做了一些提高，这是因为实验观察到：一开始训练的时候，teacher 对于目标域的判断并不果断，即分类结果更多聚集在分类边界附近，而不是类别中心。表现为：the highest probability if not obvious.
        作者受启发于 RevGradRevGradRevGrad，提出了下面的公式（因为不熟悉这篇工作，所以本 UP 还不能理解）
min⁡θmax⁡ϕLd(XS,XT)=1N∑i=1N[log⁡c(f(xSi;θ);ϕ)]+1M^∑i=1M^[γi×log⁡(1−c(f(xTi;θ);ϕ))](8)\min_{\theta}\max_{\phi}\mathcal L_d(\mathcal X_S,\mathcal X_T)={1\over N}\sum_{i=1}^N[\log c(f(x_S^i;\theta);\phi)]+{1\over{\hat M}}\sum_{i=1}^{\hat M}[\gamma_i \times \log(1-c(f(x_T^i;\theta);\phi))]\\\tag 8θmin​ϕmax​Ld​(XS​,XT​)=N1​i=1∑N​[logc(f(xSi​;θ);ϕ)]+M^1​i=1∑M^​[γi​×log(1−c(f(xTi​;θ);ϕ))](8)        其中，当且仅当 teacher 对目标域 xTix_T^ixTi​ 的判断概率超过阈值 ppp 后，γi=1\gamma_i=1γi​=1.

根据作者描述，上面这一项的特点是：当两个域之间的散度越来越小，即隐空间下域越近，就会有跟多的目标域数据参与到训练中。

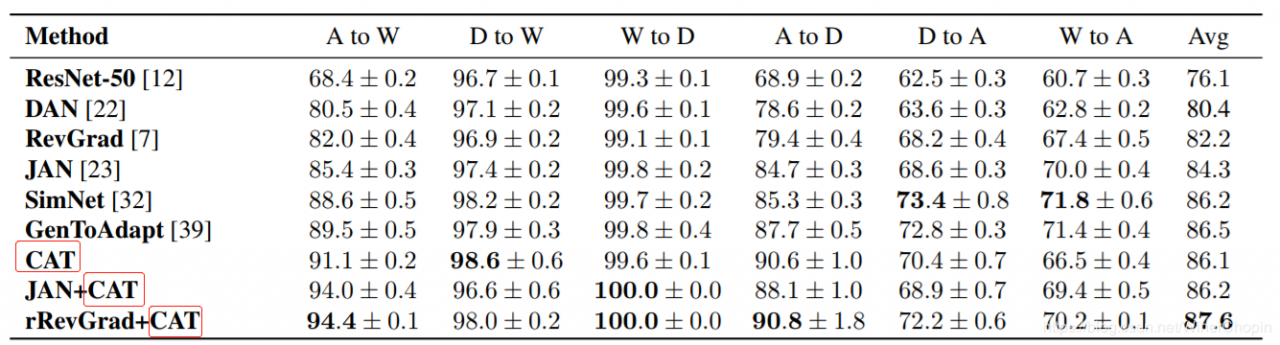
        结果当然是作者的新的模块结合其他的方法吊打其他人。

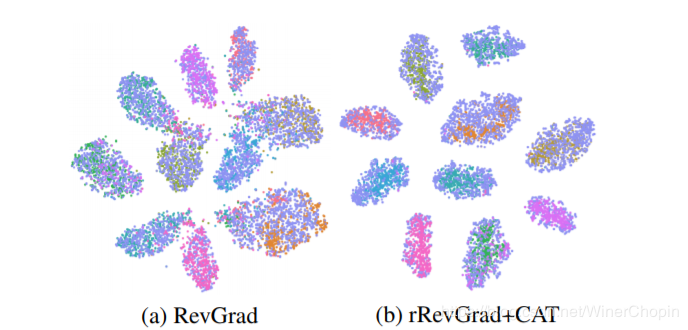
        作者可视化了 fff 的特征分布，发现加上新的模块后，特征之间的“同类相近、异类相斥”的效果更加明显，说明了上面两个 losseslosseslosses 是起作用的。

cluster for with domain