2020-BNUZ-IT节程序设计竞赛网络赛题解

目录总述题目来源 ：A. 这道生物题明明超简单却过分思考B. 我们仍未知道那天所听闻的Reader的名字C. 棋之高手成名录D.因为太怕输就全点攻击力了E. 因为感觉打不过就全点速度与攻击了F. Re：从零开始的元神游戏生活G. 在大学里安排座位是否搞错了什么H. 最强士兵的养成方法I. 防AK是简单知识点，这样的题目你喜欢吗？J. 关于nsy辍学这档事K. 数学老师想让我交钱\~师生间的对线头脑战~L. 我的数据结构不可能这么难M. 沉迷游戏少年不会梦到数学题答案
总述

  首先，映入大家眼帘的是，我们对题目标题进行了整活。（嗯？怎么有的人做着做着题就打开了bilibili？） 方便让不会做的同学去补番，番剧对照表如下：（一开口就知道老二刺螈了，听说有人Diss我纯死宅，在？出来对线？）

  我们对这套题的估测，考虑部分同学的不重视的原因，只计算有效提交参赛者，猜测90%的参赛者能过2题以上，60%的参赛者能过4题以上，10%的参赛者能过8题以上。上述仅为个人猜测，请以实际情况为准。
  题目类型包括：模拟(A/C/暴力G/I)，思维(F)，数学(E)，数据结构(标程G/J/L)，字符串处理(K)，算法(B/D/H/M)。
  本次题解将给出所有C/C++代码，部分Java和Python代码。看出题人懒不懒以及玄学判题机让不让过。 实名Diss判题机的Java、Python的评测速度。玄学判题机，在线歧视Java和Python选手。
  我把内存条含在嘴里，然后用脑子判题都比它快.jpg

全场最佳

题目来源 ：

2020-BNUZ-IT节程序设计竞赛网络赛

A. 这道生物题明明超简单却过分思考

Solution
  给出一个字符串，只包含大写英文字母，每次操作可以使其中一个字母依照字母表的顺序“往前变”和“往后变”，比如“A”往后变为“B”，往前变为“Z”。询问如何变化可以以最少操作次数使字符串中出现“ATCG”这一子串。
  数据量很小，暴力循环判断即可通过。不过要注意的就是一个字母可以“往前变”，也可以“往后变”，所以在判断操作次数的时候，需要分别在“往前变”所需操作次数和“往后变”所需操作次数两者中取最小值。

AC_Code (C)

#include #include #include #include int myMin(int a, int b) { if(a > b) return b; else return a; } int main() { int t; while(~scanf("%d",&t)) { for(int cas = 1; cas <= t; cas++) { int n; char str[1000]; scanf("%d",&n); scanf("%s", str); int a,c,t,g, sum, minSum = 99999; for(int i = 0; i sum) minSum = sum; } printf("Case #%d:\n%d\n", cas,minSum); } } return 0; }

AC_Code (Java)

import java.util.Scanner; public class Test5 { public static int min(int a,int b){ if(a<b) return a; return b; } public static void main(String[] args) { Scanner scanner = new Scanner(System.in); while(scanner.hasNext()){ int T = scanner.nextInt(); for(int cas=1;cas<=T;cas++){ int n = scanner.nextInt(); String ch = scanner.next(); char[] str = ch.toCharArray(); int a,c,t,g,sum,minSum = 0x3f3f3f3f; for(int i=0;i sum){ minSum = sum; } } System.out.printf("Case #%d:\n",cas); System.out.println(minSum); } } } }
B. 我们仍未知道那天所听闻的Reader的名字

Solution
  图论算法之最短路。
  给出一张无向稀疏图，选择三个点a,b,c，使得a->b->c的最短路在图中最大化。如果最多只有两个点相连则输出-1.
  基本上算是最短路板题，用邻接表存储图，枚举中间点b跑n次Dijkstra，排序dis数组取最大两个值的和，更新最大值。
  附上俺焦哥的名人名言 (圣经) ：
  

AC_Code (C++)

#include using namespace std; typedef long long ll; const int N=1111; const int M=1e5+5; const int INF=0x3f3f3f3f; int n,m; struct edge { int nxt,to,va; } e[2222]; int head[N],cnt; void addedge(int a,int b,int c) { e[++cnt].nxt=head[a]; e[cnt].to=b; e[cnt].va=c; head[a]=cnt; } int dis[N]; bool vis[N]; int ans=0; bool cmp(int a,int b) { return a>b; } int Dijkstra(int s) { memset(vis, 0, sizeof(vis)); memset(dis, INF, sizeof(dis)); dis[s]=0; priority_queue<pair >q; q.push({-dis[s],s}); while(!q.empty()) { int u=q.top().second; q.pop(); if(!vis[u]) { vis[u]=1; for(int i=head[u]; i; i=e[i].nxt) { int v=e[i].to; if(dis[v]>dis[u]+e[i].va) { dis[v]=dis[u]+e[i].va; q.push({-dis[v],v}); } } } } sort(dis+1,dis+n+1,cmp); int x=0; for(int i=1; i<n-1; i++) { if(dis[i]!=INF&&dis[i+1]!=INF) return dis[i]+dis[i+1]; } return -1; } int main() { int t, cas=1; scanf("%d", &t); while(t--) { scanf("%d%d", &n, &m); ans=-1; cnt=0; memset(head,0,sizeof(head)); for(int i=1; i<=m; i++) { int a,b,c; scanf("%d%d%d", &a, &b, &c); addedge(a,b,c); addedge(b,a,c); } for(int i=1; i<=n; i++) { ans=max(Dijkstra(i),ans); } printf("Case #%d:\n%d\n", cas++, ans); } }
C. 棋之高手成名录

Solution
考虑将被将军的情况：

棋子落在与将同一横轴的点上将军 棋子落在与将同一纵轴的点上将军 棋子与将位置呈“日”字

满足第一或第二个条件的棋子有炮、车、兵（卒），满足第三个条件的棋子有马。
（PS：士、象、帅本身不具有将军的能力）

因此，只要枚举将的横轴、纵轴以及8个日字格上的棋子有没有能够将军的棋子即可。

AC_Code (C++)

#include #define FOR(I, A, B) for (int I = (A); I <= (B); ++I) #define CASET int ___T; scanf("%d", &___T); for(int cs=1;cs= 1 && x = 1 && y = 1 && x = 1 && y = 1 && x = 1 && y = 1 && x = 1 && y > n; FOR(i,1,10) { scanf("%s",s[i]+1); } printf("Case #%d:\n",cs); solve(); } }
D.因为太怕输就全点攻击力了

Solution
  如果自身攻击力比对方高则不受伤害，否则受到攻击力差值的伤害。
  贪心算法题，只需要对比特化前tq和特化后th收到的伤害差cha多少，差值越大说明此次特化收益越高。将特化前的攻击力tq、特化后的攻击力th、差值cha，进行差值从大到小的结构体排序，选择前m个特化后，选择n-m个特化前即可。

AC_Code (C++)

#include #include using namespace std; const int maxn = 1010; int df[maxn],ds[maxn]; struct node { int tq,th,cha; }c[maxn]; bool cmp(node a, node b) { return a.cha > b.cha; } int main() { int t, cas = 0; scanf("%d",&t); while(t--) { int n,m; scanf("%d%d",&n,&m); for(int i=0;i<n;i++) { scanf("%d",&df[i]); } for(int i=0;i<n;i++) { scanf("%d",&ds[i]); c[i].tq = ds[i] - df[i]; c[i].th = ds[i] - 2*df[i]; if(c[i].tq < 0) c[i].tq = 0; if(c[i].th < 0) c[i].th = 0; c[i].cha = c[i].tq - c[i].th; } sort(c,c+n,cmp); long long ans = 0; for(int i=0;i<m;i++) { ans += c[i].th; } for(int i=m;i<n;i++) { ans += c[i].tq; } printf("Case #%d:\n",++cas); printf("%lld\n",ans); } }

AC_Code (Python)

from functools import cmp_to_key t = int(input()) c = [] for o in range(t): c.clear() n, m = map(int, input().split()) df = list(map(int, input().split())) ds = list(map(int, input().split())) for i in range(n): ii = ds[i]-df[i] if ds[i]-df[i] > 0 else 0 jj = ds[i]-2*df[i] if ds[i]-2*df[i] > 0 else 0 c.append([ii-jj, ii, jj]) c.sort(key=cmp_to_key(lambda a, b: b[0]-a[0])) ans = 0 for i in range(0, m): ans += c[i][2] for i in range(m, n): ans += c[i][1] print("Case #{}:\n{}".format(o+1, ans))
E. 因为感觉打不过就全点速度与攻击了

Solution
  小陈由于血量很低，所以只能在「无敌金身」的10秒内击败敌人，否则就会被打败。给你一组敌人的血量，问你能不能打败敌人。
  首先，此题的思路就是找到最大的总攻击值，只要敌人血量小于等于最大总攻击值，就会被击败。
  假设使用如下情况：
    使用「无敌金身」「超加速」：10回合造成伤害10x100x70x120%=84000
    使用「无敌金身」「超加速」「光速神言」触发「虚影」：咏唱5回合，剩下5回合造成伤害5x100x2x70x170%=119000
  明显是第二种造成伤害更多，所以我们只需要以第二种情况作为区分即可。
此题容易卡住的点

题目太长不想读，以为是难题（其实是一篇阅读理解） C++使用cin导致超时 开了数组，并且因为数组开小了，导致运行时错误 开了动态数组导致超时 判断条件太多导致超时 Java由于Scanner耗费时间过长，这里我们需要用到快读（玄学判题机在线歧视Java选手）

AC_Code (C)

#include int main(){ int T; scanf("%d",&T); for(int o=0;o<T;o++){ int n; scanf("%d",&n); printf("Case #%d:\n",o+1); int a; for(int i=0;i<n;i++){ scanf("%d",&a); if(a<=119000) printf("Yes\n"); else printf("No\n"); } } return 0; }

AC_Code (Java)

import java.io.*; import java.util.StringTokenizer; import java.math.BigInteger; public class Test4 { public static void main(String[] args) { InputStream inputStream = System.in;//InputStream是表示字节输入流的所有类的超类 OutputStream outputStream = System.out; //InputStream与System 没有关系.System.in是System 这个类的静态变量，只是in是InputStream类型的 InputReader sc = new InputReader(inputStream); PrintWriter out = new PrintWriter(outputStream); Task solver = new Task(); solver.solve(sc, out);//这里当作原来的Main函数，输入输出都在里面解决 out.close();//关闭输出流 } static class Task { public void solve(InputReader scan, PrintWriter out) { int t=scan.nextInt(); for(int i=0;i<t;i++) { out.printf("Case #%d:\n",i+1); int n=scan.nextInt(); while(n!=0) { int a=scan.nextInt(); if(a<=119000){ out.println("Yes"); }else{ out.println("No"); } n--; } } // out.println(ans);//输出答案 } } //自己写出Scanner原本的输入语法，封装在InputReader类里 static class InputReader { public BufferedReader reader; public StringTokenizer tokenizer; public InputReader(InputStream stream) { reader = new BufferedReader(new InputStreamReader(stream), 32768); //32768是输入缓冲区大小，随便设的 tokenizer = null; } public String next() { while (tokenizer == null || !tokenizer.hasMoreTokens()) { try { tokenizer = new StringTokenizer(reader.readLine()); } catch (IOException e) { throw new RuntimeException(e); } } return tokenizer.nextToken(); } public int nextInt() { return Integer.parseInt(next()); } public long nextLong() { return Long.parseLong(next()); } public double nextDouble() { return Double.parseDouble(next()); } public boolean hasNext() { try { String string = reader.readLine(); if (string == null) { return false; } tokenizer = new StringTokenizer(string); return tokenizer.hasMoreTokens(); } catch (IOException e) { return false; } } public BigInteger nextBigInteger() {//大数 return new BigInteger(next()); } } } //加速板参照 https://www.cnblogs.com/shoulinniao/p/12113790.html

AC_Code (Python)

T = int(input()) for i in range(T): n = int(input()) print("Case #{}:".format(i+1)) a = input().split() for ii in a: if int(ii) <= 119000: print("Yes") else: print("No")
F. Re：从零开始的元神游戏生活

Solution
  P.S. 出题人真的是在玩《原神》的时候突然想到的题目。题设也全是真的
  岩元素只能和岩元素反应，雷元素只能和水元素反应。所以我们优先处理这两个，只需要找对面的元素组是否符合：对方岩元素=我方岩元素，对方水元素≥我方雷元素，我方水元素≥对方雷元素即可。如果不符合，则不可能完全反应。
  然后就是处理水、火、冰元素，这三种元素可以互相反应。因此，只要判断我方的任意两个元素，是否大于对方的第三个元素即可。

AC_Code (C++)

#include using namespace std; int main() { int t, cas = 0; cin >> t; while(t--) { int n; int ele1[10],ele2[10]; memset(ele1,0,sizeof(ele1)); memset(ele2,0,sizeof(ele2)); string str1,str2; cin >> n; cin >> str1; cin >> str2; for(int i=0; i<n; i++) { if(str1[i] == 'i') { ele1[0]++; } if(str1[i] == 'f') { ele1[1]++; } if(str1[i] == 'w') { ele1[2]++; } if(str1[i] == 't') { ele1[3]++; } if(str1[i] == 'r') { ele1[4]++; } } for(int i=0; i= ele2[3] && ele2[2] >= ele1[3]) { ele1[2] -= ele2[3]; ele2[2] -= ele1[3]; } else { flag = false; } if(ele1[0] + ele1[1] < ele2[2] || ele1[2] + ele1[1] < ele2[0] || ele1[0] + ele1[2] < ele2[1]) { flag = false; } if(ele2[0] + ele2[1] < ele1[2] || ele2[2] + ele2[1] < ele1[0] || ele2[0] + ele2[2] < ele1[1]) { flag = false; } printf("Case #%d:\n",++cas); if(flag) { puts("YES"); } else { puts("NO"); } } }

AC_Code (Java)

import java.util.Scanner; public class Test1 { public static int conversion(char ch){ if(ch=='i') return 0; if(ch=='f') return 1; if(ch=='w') return 2; if(ch=='t') return 3; if(ch=='r') return 4; return -1; } int min(int a,int b){ if(a>b){ return a; } return b; } public static void main(String[] args) { Scanner scanner = new Scanner(System.in); int T = scanner.nextInt(); for(int x=0;x<T;x++){ int n = scanner.nextInt(); String ch1 = scanner.next(); String ch2 = scanner.next(); int[] ele1 = new int[5]; int[] ele2 = new int[5]; for (int i=0;i<5;i++){ ele1[i] = ele2[i] = 0; } for(int i=0; i<n; i++) { ele1[conversion(ch1.charAt(i))]++; ele2[conversion(ch2.charAt(i))]++; } int flag = 0; if(ele1[4]!=ele2[4]){ flag=1; } if(!(ele1[3]<=ele2[2]&&ele2[3]<=ele1[2])) { flag=1; } else { ele1[2] -= ele2[3]; ele2[2] -= ele1[3]; } //i f w if(ele1[0] <= ele2[1] + ele2[2] &&ele1[1] <= ele2[0] + ele2[2] &&ele1[2] <= ele2[0] + ele2[1]) { } else { flag = 1; } System.out.printf("Case #%d:\n",x+1); if(flag==0) { System.out.println("YES"); } else { System.out.println("NO"); } } } }

AC_Code (Python)

t = int(input()) for o in range(t): n = int(input()) str1 = input() str2 = input() ele1 = [str1.count('i'), str1.count('f'), str1.count('w'), str1.count('t'), str1.count('r')] ele2 = [str2.count('i'), str2.count('f'), str2.count('w'), str2.count('t'), str2.count('r')] flag = True if ele1[4] != ele2[4]: flag = False if ele1[2] >= ele2[3] and ele2[2] >= ele1[3]: ele1[2] -= ele2[3] ele2[2] -= ele1[3] else: flag = False if ele1[0] + ele1[1] < ele2[2] or ele1[2] + ele1[1] < ele2[0] or ele1[0] + ele1[2] < ele2[1]: flag = False if ele2[0] + ele2[1] < ele1[2] or ele2[2] + ele2[1] < ele1[0] or ele2[0] + ele2[2] < ele1[1]: flag = False print("Case #{}:\n{}".format(o+1, "YES" if flag else "NO"))
G. 在大学里安排座位是否搞错了什么

Solution

本题本准备卡暴力的，但是因为考虑java选手减小了数据。因此本题暴力可解。 此处题解会给出暴力和正解的代码，但是仅给出正解的思路。 考察：滑动窗口，双向队列 滑动窗口可以将嵌套的循环问题，转换为单循环问题，降低时间复杂度。 本题思路：

将题目归纳得：给出一个长为n的字符串，有两个操作，操作二是读取第x位的字符串。操作一是翻转包括x的之后m个字符。

对于操作一来说，大量的遍历是很容易TLE的，所以最好的选择是不翻转字符串，而是利用一个flag判断当前要从子串的哪端读取 来模拟翻转，这样可以在大数据的情况下极大的减少时间复杂度。

因此可以新创建一个环形队列或者双向队列来储存子串。如图

当读取到被反转的那段字符串时先判断flag的值，再从新的数组读取相对位置的字符。

又因为题中有保证x1<=x2<=x3<=….<=n-m+1，因此就是持续向右的滑动，滑动的操作也是将此时子串的 “左端” 取出插入到相应位置，然后取值插入子串相应的”右端“

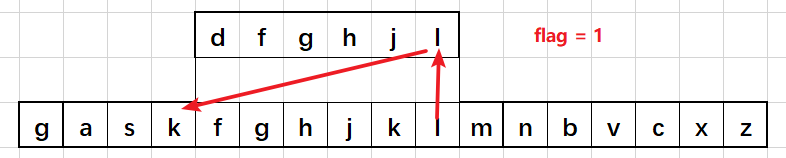
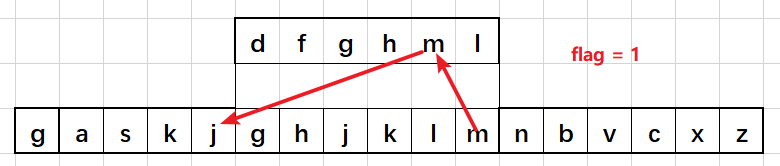
下面是滑动窗口的举例（最开始的flag为0），演示这里使用的是环形队列

AC_Code (C++暴力)

#include #include #include #include using namespace std; int main() { ios::sync_with_stdio(false), cin.tie(0), cout.tie(0); int n,m,q,cas=1,op,pos; char ch[1000005]; while(cin >> n >> m >> q) { cin >> ch; vector v; for(int i=0; i<strlen(ch); i++) { v.push_back(ch[i]); } printf("Case #%d:\n",cas++); for(int i=0; i> op >> pos; if(op==2) { printf("%c",v[pos-1]); } else { reverse(v.begin()+pos-1,v.begin()+pos+m-1); } } puts(""); } }

AC_Code (C++标程)

#include using namespace std; const int maxn = 1e6 + 500; int n,m,q,swq,now; char s[maxn],str[maxn]; int main() { int count = 1; while(~scanf("%d %d %d",&n,&m,&q)) { swq = 0; now = 0; dequedq; scanf("%s",str); strcpy(s+1,str); cout<<"Case #"<<count++<<":"<<endl; for(int i=1; i<=m; i++) { dq.push_back(str[i-1]); } now=1; for(int i=1; i<=q; i++) { int op,id; scanf("%d%d",&op,&id); if(op==2) { if(idnow+m-1)putchar(s[id]); else { id-=now; if(swq)putchar(dq[m-1-id]); else putchar(dq[id]); } } else { while(now<id) { if(swq) { s[now]=dq.back(); dq.pop_back(); dq.push_front(str[now+m-1]); } else { s[now]=dq.front(); dq.pop_front(); dq.push_back(str[now+m-1]); } now++; } swq^=1; } } cout<<endl; } }
H. 最强士兵的养成方法

Solution
  背包算法。
  该题是一个二维费用+分组+01背包，设dp[i][j][k]表示枚举到前i个国家花费j元购买k件商品获得的最大战斗力，状态转移方程为：
  dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j-vi][k-1]+wi)。
  但由于直接开三维dp会爆内存，因此必须压缩掉一维，新的状态转移方程为：
  dp[j][k] = max(dp[j][k], dp[j-v[i]][k-1]+w[i])。

AC_Code (C++)

#include using namespace std; typedef long long ll,LL; #define CASET int T; cin >> T; while(T--) const int maxn = 1002; ll n,Q,M; ll dp[maxn][maxn]; ll ans; ll v[maxn],w[maxn]; void Pack(int s) { for(int j=Q; j>=0; --j) { for(int k=M; k>=1; --k) { for(int i=1; i= v[i]) { dp[j][k] = max(dp[j][k], dp[j-v[i]][k-1]+w[i]); } } } } } void solve() { memset(dp,0,sizeof(dp)); scanf("%lld%lld%lld",&n,&Q,&M); for(ll i=1; i<=n; ++i) { ll s; scanf("%lld",&s); for(ll j=1; j<=s; ++j) { scanf("%lld%lld",&v[j],&w[j]); } Pack(s); } printf("Case #%lld:\n%lld\n", ++ans, dp[Q][M]); } int main() { CASET {solve();} }
I. 防AK是简单知识点，这样的题目你喜欢吗？

Solution
  假的防AK，真的签到题。让你判断他到底坐了多少次车，只需要判断有多少次在不同教学楼之间来回，然后取相对多的一次。
  把字符串进行处理，判断str[i] != str[i+1]，然后(count+1) / 2即可。
  非常感谢大家热心帮助数学白痴苏铭同学计算车费，贴张图表示重谢，如引起当事人不适，可以联系群里的答疑姬进行删除。
  

AC_Code (C)

#include #include int main() { int n,len; char ch[10005]; while(~scanf("%d",&n)) { for(int i=0; i<n; i++) { scanf("%d",&len); scanf("%s",ch); int count = 0; for(int j=0; j<len-1; j++) { if(ch[j]!=ch[j+1]) { count++; } } printf("Case #%d:\n",i+1); printf("%d\n",count/2+(count%2==0?0:1)); } } }

AC_Code (Java)

import java.util.Scanner; public class Test3 { public static void main(String[] args) { Scanner scanner = new Scanner(System.in); int cas=1; while (scanner.hasNext()){ int n = scanner.nextInt(); for(int j=0;j<n;j++){ int m = scanner.nextInt(); String ch = scanner.next(); int count=0; for (int i=0;i<ch.length()-1;i++){ if(ch.charAt(i)!=ch.charAt(i+1)){ count++; } } System.out.printf("Case #%d:\n",cas++); System.out.printf("%d\n",count/2 + (count%2==0?0:1)); } } } }

AC_Code (Python)

n = int(input()) for o in range(n): le = int(input()) ch = input() ans = 0 print("Case #{}:".format(o+1)) for i in range(0, le - 1): if ch[i] != ch[i + 1]: ans += 1 if ans % 2 == 1: ans += 1 print(ans // 2)
J. 关于nsy辍学这档事

Solution
  从2019国庆欢乐赛开始延续至今每次比赛都有的nsy系列故事，应该至此要告一段落了。这次是专门为nsy大佬出的题，可惜他没能写出来。可能明年IT节现场赛还会有后传吧。
  数据结构+小优化，但是专业课应该不会学到这个东西，知识点为：树上启发式合并。数据因为要出成树状结构，但是生成器懒得写那么复杂，所以其实很多情况没有考虑到，不是特别严谨。后来发现oj有bug，不会判Java的MLE。因此有北理的同学使用Java直接开出40000×40000的空间过了，但是后来修完bug之后被重判了。（带恶人）
  思路是使用dfs往下搜索，搜到底之后不断与父节点进行合并，用集合set进行所有小弟编号的存取，然后小集合进入大集合，只对变化的区间进行修改，可以优化很多时间。
  如果使用暴力的话，会被一条40000的长链卡住，但是其他情况跑的比我标程还快。（图为不包含长链的情况，测试数据并非最终版本，实际时长不超过1s，但是开了2s）

  其实正解应该是直接寻找小集合进入大集合，时间复杂度为O(nlogn)。但是我的标程默认集合u为大集合，否则交换u、v集合的位置，因此时间复杂度实际为O(nlog2n).

AC_Code (C++)

#include using namespace std; typedef long long ll; const int maxn = 40010; #define sz(x) ((int)x.size()) int p[maxn]; set s[maxn]; set::iterator it, jt; vector son[maxn]; ll ans[maxn]; inline ll sq(ll a, ll b) { return (b+a)*(b+a); } void Insert(int u, int x) { it = s[u].lower_bound(x); jt = s[u].upper_bound(x); if (it != s[u].begin() && jt != s[u].end()) { //如果合进来的数在中间 int l = *(--it), r = *jt; ans[u] += - sq(l, r) + sq(l, x) + sq(x, r); } else if (s[u].empty()) { //如果这是叶子节点则是空的 s[u].insert(x); return; } else if (it == s[u].begin() && jt != s[u].end()) { //如果合进来的数在头部 int r = *jt; ans[u] += sq(x, r); } else if (it != s[u].begin() && jt == s[u].end()) { //如果合进来的数在尾部 int l = *(--it); ans[u] += sq(l, x); } s[u].insert(x); } void dfs(int u) { ans[u] = 0; for (int i = 0; i < sz(son[u]); i++) { int v = son[u][i]; dfs(v); //如果还能继续搜则往下 /* 因为懒得寻找大集合，默认u为大集合，不符合的话，交换大小集合 */ if (sz(s[u]) > t; while(t--) { int n; cin >> n; memset(p,0,sizeof(p)); memset(ans,0,sizeof(ans)); for(int i=0;i<maxn;i++) { s[i].clear(); son[i].clear(); } for (int i = 2; i > p[i]; son[p[i]].push_back(i); //记录编号i为编号p[i]的子节点 } dfs(1); //从根节点进行搜索 printf("Case #%d:\n",++cas); for (int i = 1; i <= n; i++) { printf("%lld\n", ans[i]); } } }
K. 数学老师想让我交钱~师生间的对线头脑战~

Solution
  给出三元一次方程，要求将三个方程多项式合并成固定的格式Ax+By+Cz=D
  这算是一个较为复杂的模拟题，首先要能够将字符串转化成数字，还要判断前面的正负号（前面没+就是正数），然后将对应的数字赋值给x,y,z，等于号的左右两边也有数字，最后要进行运算把数字放到右边。最后输出答案的时候还要注意第一位未知数如果是正数的话就不用输出+

AC_Code (C++)

#include #include #include using namespace std; char s1[100],s2[100],s3[100]; void solve(char s[],int *a,int *b,int *c,int *d) { int temp = 0; int len = strlen(s); bool flag = true; for(int i=0; i<len; i++) { if(s[i]='0') temp = temp*10+(s[i]-'0'); else if(s[i]=='x') { if(temp==0) temp=1; if(!flag) temp=-temp; *a = temp; temp = 0; flag = true; } else if(s[i]=='y') { if(temp==0) temp=1; if(!flag) temp=-temp; *b = temp; temp = 0; flag = true; } else if(s[i]=='z') { if(temp==0) temp=1; if(!flag) temp=-temp; *c = temp; temp = 0; flag = true; } else if(s[i]=='-') { flag = false; } else if(s[i]=='=') { if(!flag) temp=-temp; *d = temp; temp = 0; } } if(!flag) temp=-temp; *d = -(*d)+temp; return; } int main() { int T,cas = 1; scanf("%d",&T); while(T--) { int a1=0,a2=0,a3=0,b1=0,b2=0,b3=0,c1=0,c2=0,c3=0,d1=0,d2=0,d3=0; scanf("%s",s1); scanf("%s",s2); scanf("%s",s3); solve(s1,&a1,&b1,&c1,&d1); solve(s2,&a2,&b2,&c2,&d2); solve(s3,&a3,&b3,&c3,&d3); printf("Case #%d:\n",cas++); int A=a1+a2+a3,B=b1+b2+b3,C=c1+c2+c3,D=d1+d2+d3; if(A!=0) { if(A==1) printf("x"); else if(A==-1) printf("-x"); else printf("%dx",A); } if(A!=0&&B>0) printf("+"); if(B!=0) { if(B==1) printf("y"); else if(B==-1) printf("-y"); else if(B>1) printf("%dy",B); else printf("%dy",B); } if((A!=0||B!=0)&&C>0) printf("+"); if(C!=0) { if(C==1) printf("z"); else if(C==-1) printf("-z"); else if(C>1) printf("%dz",C); else printf("%dz",C); } printf("=%d\n",D); } return 0; }
L. 我的数据结构不可能这么难

Solution
  对一个序列有四种操作，插入头元素、删除头元素、插入头元素、删除尾元素。
  图片和题目已经提示的很明显了，就是让大家使用链表，基本上学过数据结构的同学，直接拿链表的作业改一改就可以用了。学过c++STL的同学直接用头文件也可以。算是传统签到题（在？看着过题率好好说话？），但是要注意多组数据输入，要记得清空链表。（才不会告诉你出题人就是忘记清空所以一开始大家都WA3，虽然后来重判了但还是搞人心态啊喂，接下来有请出题人表演铁锅炖自己）

AC_Code (C++)

#include #include using namespace std; int main() { int T,cas = 1; scanf("%d",&T); while(T--) { list lt; int n,m; scanf("%d",&n); for(int i=0;i<n;i++) { int a; scanf("%d",&a); lt.push_back(a); } scanf("%d",&m); for(int i=0;i<m;i++) { int x,y; scanf("%d",&x); if(x==1) { scanf("%d",&y); lt.push_front(y); } else if(x==2) { lt.erase(lt.begin()); } else if(x==3) { scanf("%d",&y); lt.push_back(y); } else { lt.erase(--lt.end()); } } int l,r; scanf("%d %d",&l,&r); int i=1; printf("Case #%d:\n",cas++); for(list::iterator it = lt.begin(); it != lt.end(); ++it,i++) { if(i>=l&&ir) break; } puts(""); } return 0; }
M. 沉迷游戏少年不会梦到数学题答案

Solution
  数论算法之矩阵快速幂。但是由于该题的数列呈线性，也可使用递推板过题。因该解法不为正解，此处不提供递推板的代码，请自行百度。
  递推式是f(n) = f(n-1) + 2 * f(n-2) + n3 + 2 * n + 1，其中n>2.已知：f(1) = 0，f(2) = 1.
  题目的n最大为1e16，m最大为1e2，用普通的递归和普通迭代是肯定会TLE的，所以要用矩阵快速幂来减少时间复杂度，注意在写递推矩阵要补一个n的二次方。
  矩阵图如下：

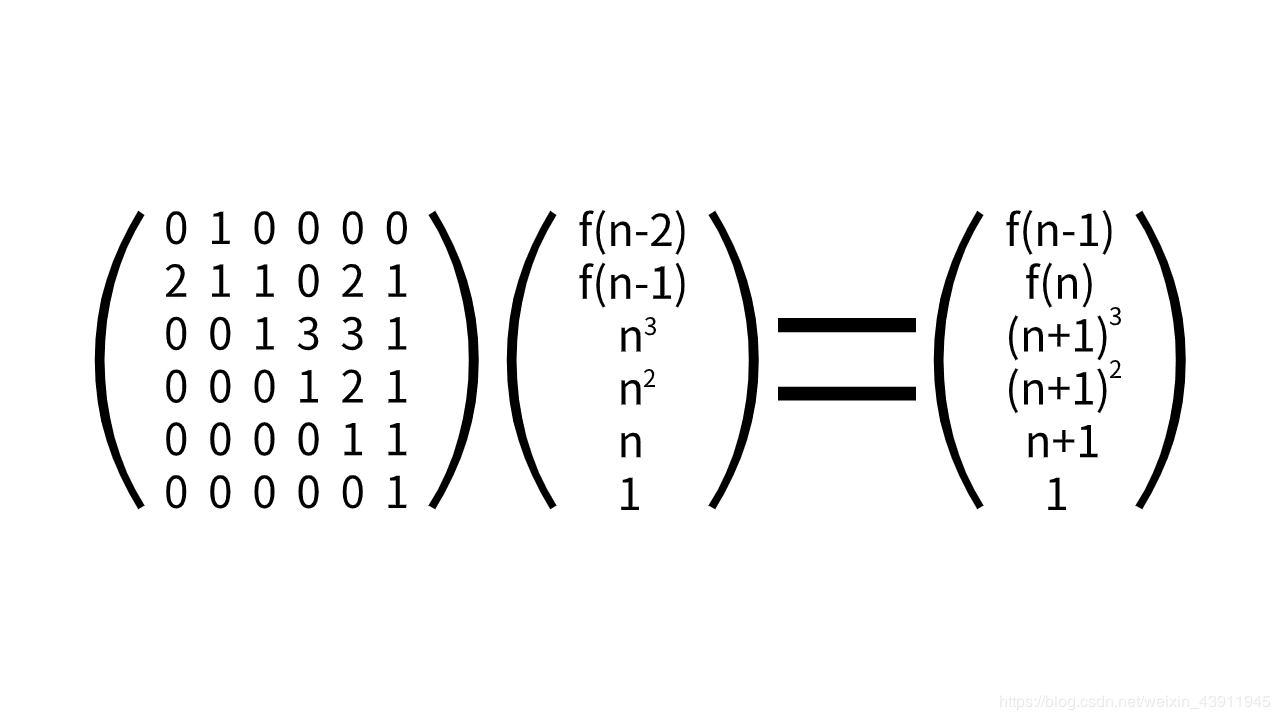
  还记得俺焦哥曾经说过 (圣经)：
  

AC_Code (C++)

#include #include const int Mod = 1000000007; typedef long long ll; using namespace std; class Matrix { public: ll **mat_; int rows_; int cols_; Matrix(const Matrix &matrix) { rows_ = matrix.rows_; cols_ = matrix.cols_; mat_ = new ll*[rows_]; for (int i = 0; i < rows_; i++) { mat_[i] = new ll[cols_]; } for (int i = 0; i < rows_; i++) { for (int j = 0; j < cols_; j++) { mat_[i][j] = matrix.mat_[i][j]; } } } Matrix(int rows, int cols) { rows_ = rows; cols_ = cols; mat_ = new ll*[rows]; for (int i = 0; i < rows; i++) { mat_[i] = new ll[cols]; } } Matrix(int rows, int cols, ll init) { rows_ = rows; cols_ = cols; mat_ = new ll*[rows]; for (int i = 0; i < rows; i++) { mat_[i] = new ll[cols]; } for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { mat_[i][j] = init; } } } static Matrix zeros(int rows,int cols) { Matrix m(rows,cols,0); return m; } static Matrix eye(int size) { Matrix m = zeros(size, size); for(int i=0;i<size;i++) { m.mat_[i][i] = 1; } return m; } friend Matrix operator * (const Matrix &matrix1, const Matrix &matrix2) { Matrix m(matrix1.rows_, matrix2.cols_); ll temp; for(int i=0; i<m.rows_; i++) { for(int j=0; j<m.cols_; j++) { ll sum = 0; for(int x=0; x 0) { if (k & 1) m = m * temp; temp = temp * temp; k >>= 1; } return m; } }; int main() { /* ll m1[6][6] = { {0,1,0,0,0,0}, {2,1,1,0,2,1}, {0,0,1,3,3,1}, {0,0,0,1,2,1}, {0,0,0,0,1,1}, {0,0,0,0,0,1} }; ll m2[6][1] = { {0}, {1}, {27}, {9}, {3}, {1} }; */ Matrix m1(6,6); Matrix m2(6,1); m1.mat_[0][0] = 0; m1.mat_[0][1] = 1; m1.mat_[0][2] = 0; m1.mat_[0][3] = 0; m1.mat_[0][4] = 0; m1.mat_[0][5] = 0; m1.mat_[1][0] = 2; m1.mat_[1][1] = 1; m1.mat_[1][2] = 1; m1.mat_[1][3] = 0; m1.mat_[1][4] = 2; m1.mat_[1][5] = 1; m1.mat_[2][0] = 0; m1.mat_[2][1] = 0; m1.mat_[2][2] = 1; m1.mat_[2][3] = 3; m1.mat_[2][4] = 3; m1.mat_[2][5] = 1; m1.mat_[3][0] = 0; m1.mat_[3][1] = 0; m1.mat_[3][2] = 0; m1.mat_[3][3] = 1; m1.mat_[3][4] = 2; m1.mat_[3][5] = 1; m1.mat_[4][0] = 0; m1.mat_[4][1] = 0; m1.mat_[4][2] = 0; m1.mat_[4][3] = 0; m1.mat_[4][4] = 1; m1.mat_[4][5] = 1; m1.mat_[5][0] = 0; m1.mat_[5][1] = 0; m1.mat_[5][2] = 0; m1.mat_[5][3] = 0; m1.mat_[5][4] = 0; m1.mat_[5][5] = 1; m2.mat_[0][0] = 0; m2.mat_[1][0] = 1; m2.mat_[2][0] = 27; m2.mat_[3][0] = 9; m2.mat_[4][0] = 3; m2.mat_[5][0] = 1; int m; scanf("%d",&m); ll n; for(int i=0; i=2) { Matrix m3(m1 ^ (n - 1)); Matrix m4(m3 * m2); printf("%lld\n",m4.mat_[0][0]); } else { printf("0\n"); } } }

AC_Code (Java)

import java.math.BigInteger; import java.util.Scanner; public class Matrix { public BigInteger mat[][]; public int rows; public int cols; public static final BigInteger MOD = new BigInteger("1000000007"); public static final BigInteger ZERO = new BigInteger("0"); public static final BigInteger ONE = new BigInteger("1"); public Matrix() { } public Matrix(int rows, int cols) { this.rows = rows; this.cols = cols; mat = new BigInteger[rows][cols]; } public Matrix(Matrix m) { this.rows = m.rows; this.cols = m.cols; this.mat = new BigInteger[rows][cols]; for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { this.mat[i][j] = m.mat[i][j]; } } } public static Matrix multiply(Matrix m1, Matrix m2) { Matrix ans = new Matrix(m1.rows, m2.cols); for (int i = 0; i < ans.rows; i++) { for (int j = 0; j < ans.cols; j++) { BigInteger sum = new BigInteger("0"); for (int x = 0; x < m1.cols; x++) { BigInteger temp = m1.mat[i][x].multiply(m2.mat[x][j]); sum = sum.add(temp); sum = sum.mod(MOD); } ans.mat[i][j] = sum; } } return ans; } public static Matrix poww(Matrix m1, BigInteger k) { Matrix m = Matrix.eye(m1.rows); Matrix temp = new Matrix(m1); while (k.compareTo(ZERO) == 1) { if (k.and(ONE).compareTo(ZERO) == 1) { m = Matrix.multiply(m, temp); } temp = Matrix.multiply(temp, temp); k = k.shiftRight(1); } return m; } public static Matrix eye(int k) { Matrix m = new Matrix(k, k); for (int i = 0; i < k; i++) { for (int j = 0; j < k; j++) { m.mat[i][j] = ZERO; } } for (int i = 0; i < k; i++) { m.mat[i][i] = ONE; } return m; } public void print() { for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { System.out.print(mat[i][j]+" "); } System.out.println(); } } public static void main(String[] args) { Matrix m1 = new Matrix(6, 6); Matrix m2 = new Matrix(6, 1); m1.mat[0][0] = new BigInteger("0"); m1.mat[0][1] = new BigInteger("1"); m1.mat[0][2] = new BigInteger("0"); m1.mat[0][3] = new BigInteger("0"); m1.mat[0][4] = new BigInteger("0"); m1.mat[0][5] = new BigInteger("0"); m1.mat[1][0] = new BigInteger("2"); m1.mat[1][1] = new BigInteger("1"); m1.mat[1][2] = new BigInteger("1"); m1.mat[1][3] = new BigInteger("0"); m1.mat[1][4] = new BigInteger("2"); m1.mat[1][5] = new BigInteger("1"); m1.mat[2][0] = new BigInteger("0"); m1.mat[2][1] = new BigInteger("0"); m1.mat[2][2] = new BigInteger("1"); m1.mat[2][3] = new BigInteger("3"); m1.mat[2][4] = new BigInteger("3"); m1.mat[2][5] = new BigInteger("1"); m1.mat[3][0] = new BigInteger("0"); m1.mat[3][1] = new BigInteger("0"); m1.mat[3][2] = new BigInteger("0"); m1.mat[3][3] = new BigInteger("1"); m1.mat[3][4] = new BigInteger("2"); m1.mat[3][5] = new BigInteger("1"); m1.mat[4][0] = new BigInteger("0"); m1.mat[4][1] = new BigInteger("0"); m1.mat[4][2] = new BigInteger("0"); m1.mat[4][3] = new BigInteger("0"); m1.mat[4][4] = new BigInteger("1"); m1.mat[4][5] = new BigInteger("1"); m1.mat[5][0] = new BigInteger("0"); m1.mat[5][1] = new BigInteger("0"); m1.mat[5][2] = new BigInteger("0"); m1.mat[5][3] = new BigInteger("0"); m1.mat[5][4] = new BigInteger("0"); m1.mat[5][5] = new BigInteger("1"); m2.mat[0][0] = new BigInteger("0"); m2.mat[1][0] = new BigInteger("1"); m2.mat[2][0] = new BigInteger("27"); m2.mat[3][0] = new BigInteger("9"); m2.mat[4][0] = new BigInteger("3"); m2.mat[5][0] = new BigInteger("1"); Scanner scanner = new Scanner(System.in); int T = scanner.nextInt(); for (int i = 0; i < T; i++) { BigInteger number = scanner.nextBigInteger(); if (number.equals(ONE)) { System.out.println("0"); } else { Matrix m3 = new Matrix(Matrix.poww(m1, number.add(ONE.negate()))); Matrix m4 = new Matrix(Matrix.multiply(m3, m2)); System.out.println(m4.mat[0][0]); } } } }
作者：皓洲

程序设计竞赛 程序设计 程序