缺失值处理:拉格朗日插值法
在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值。这样的多项式称为拉格朗日(插值)多项式。数学上来说,拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。
本文介绍通过拉格朗日插值法进行缺失值的填充:
先用一组简单的数据看一下拉格朗日插值法
from scipy.interpolate import lagrange
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
#创建数据
x = [1,3,6,10]
y = [15,10,5,2]
#查看拟合出的差值函数
print(lagrange(x,y))
#绘制散点图
plt.scatter(x,y,color = 'darkblue')
#绘制拟合曲线
X = np.arange(15)
Y = lagrange(x,y)(X)
plt.plot(X,Y,linestyle = '--',color = 'k')
3 2
-0.003968 x + 0.2063 x - 3.274 x + 18.07
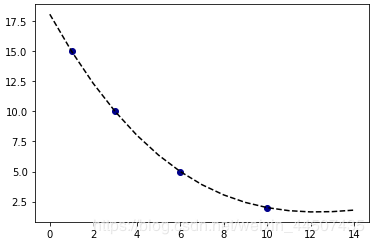
创建100个随机数的数据,并附上若干空值,查看用中位数填补缺失值和拉格朗日插值法填补缺失值的不同:
#创建数据
data = pd.Series(np.random.rand(100)*100)
data[3,6,33,56,45,66,67,80,90] = np.nan
print(data.head())
print('总数据量:{}'.format(len(data)))
print('------')
#查看数据缺失情况
data_na = data[data.isnull()]
print('缺失数据量:{}'.format(data_na))
print('缺失数据比例:{:.2f}%'.format(len(data_na)/len(data)*100))
#查看原始数据分布情况
fig = plt.figure(figsize = (20,6))
ax1 = fig.add_subplot(1,3,1)
data.plot(kind = 'kde',linestyle = '--',color = 'k',ax = ax1,title = '未填补缺失值')
#用中位数填充数据并查看填充后的分布情况
data_med = data.fillna(data.median())
ax2 = fig.add_subplot(1,3,2)
data_med.plot(kind = 'kde',linestyle = '--',color = 'r',ax = ax2,title = '中位数填补缺失值')
#用拉格朗日插值法填充缺失值并查看分布情况
data_l = data.copy()
# 创建函数,做插值,以空值前后5个数据(共10个数据)为例做插值
def fill_l(s,n,k=5):# s:需要插值的数据Series;n:需要插值的数所在的位置;k:插值的前后范围
y = s[list(range(n-k,n+1+k))]#取出前5个数与后5个数。
y = y[y.notnull()]#剔除取出的数中的空值
return lagrange(y.index,y.values)(n)
#填补缺失值
for i in range(len(data_l)):
if data_l[i] == np.nan:
data_l[i] = fill_l(data_l,i)
ax3 = fig.add_subplot(1,3,3)
data_l.plot(kind = 'kde',linestyle = '--',color = 'darkblue',ax = ax3,title = '拉格朗日填补缺失值')
0 11.555686
1 67.886859
2 64.302495
3 NaN
4 37.109191
dtype: float64
总数据量:100
------
缺失数据量:3 NaN
6 NaN
33 NaN
45 NaN
56 NaN
66 NaN
67 NaN
80 NaN
90 NaN
dtype: float64
缺失数据比例:9.00%
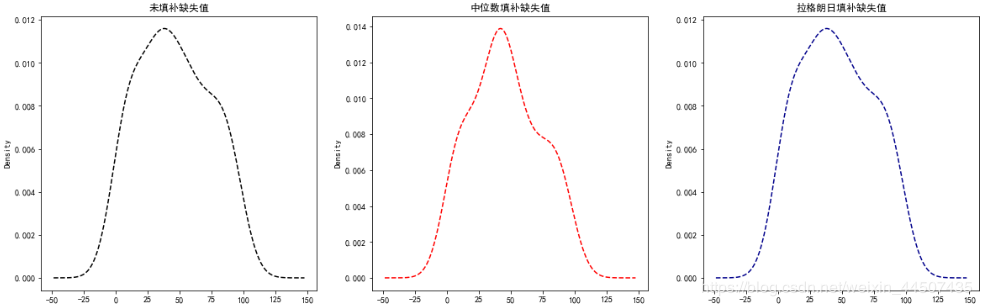
可以看到,用拉格朗日方法填充缺失值可以更好的还原数据原先的分布状态。
作者:圻子-