专题一:插值法(1)拉格朗日插值法
拉格朗日插值多项式
作者:人工智能安全爱好者
插值的定义:


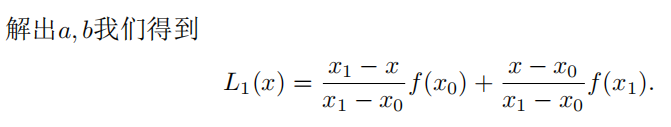
插值基函数

二次插值

n次拉格朗日插值多项式
可以由线性插值和二次插值的规律可循:
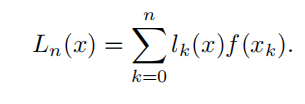
其中: 省略第k项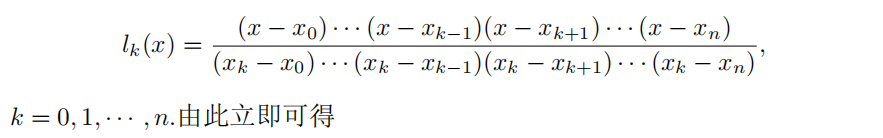
上机操作代码:
//验证拉格朗日插值法求近似值
#include
using namespace std;
//已知点坐标
struct Point
{
double x, y;
};
double LagrangeInsert(double x,Point* point, int n)
{
double temp1 = 1, temp2 = 1,result = 0;
for(int m=0;m<n;m++)
{
for (int i = 0; i < n; i++)
{
if (i != m)
{ //求分子
temp1 *= (x - point[i].x);
//求分母
temp2 *= (point[i].x - point[m].x);
}
}
//得出Lm(x)的结果
result += ((temp1 / temp2)*point[m].y);
temp1 = 1;
temp2 = 1;
}
return result;
}
//测试函数
int main()
{
Point point[100];
int n;
cout <> n;
for (int i = 0; i < n; i++)
{
cout << "No" << i+1 <<":"<< "x" <> point[i].x;
cout << "No" << i+1 <<":"<< "y" <> point[i].y;
}
cout <> x;
cout<<"Ruslt:"<<LagrangeInsert(x, point, n)<<endl;
}
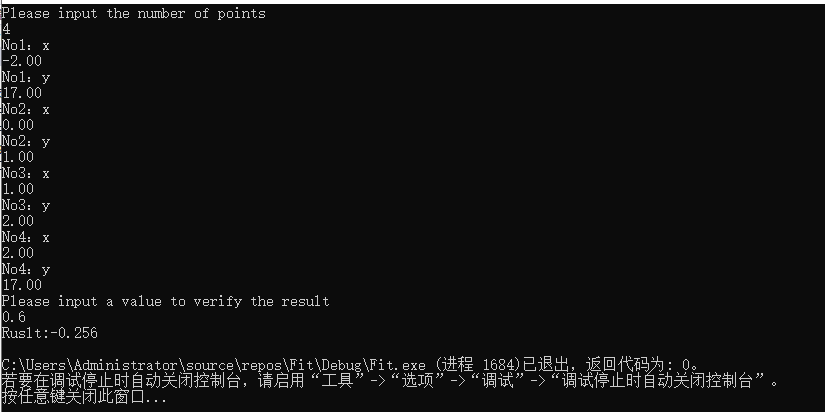
实验结果
例:
已知四个点(-2.00,17.00),(0.00,1.00),(1.00,2.00),(2.00,17.00)来计算 f(0.6)
作者:人工智能安全爱好者