validation_curve验证曲线与超参数

Phaedra ·

更新时间:2024-11-15

· 709 次阅读

validation_curve()的位置
在之前，此函数位置在sklearn.learning_curve.validation_curve()，现在，此函数的位置在sklearn.model_selection.validation_curve()。

validation_curve()的作用
我们知道误差是由偏差（bias）、方差（variance）、噪声（noise）组成。
偏差：模型对于不同的训练样本集，预测结果的平均误差
方差：模型对于不同训练样本集的敏感程度
噪声：数据集本身的一项属性
同样的数据，（cos函数上的点加上噪声），我们用同样的模型（polynomial），但是超参数却不同（degree =1,4,15）,会得到不同的拟合效果：
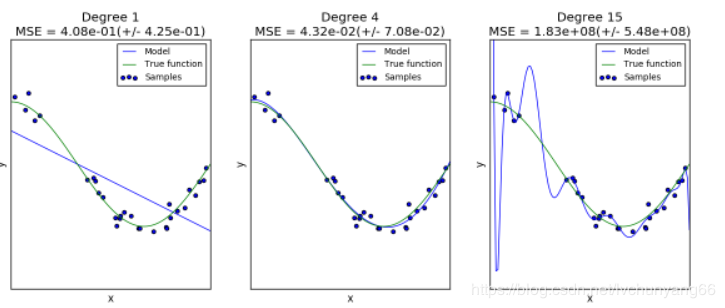
在这里插入图片描述
第一个模型太简单，模型本身就拟合不了这些数据（高偏差，underfitting）；
第二个模型可以看成几乎完美地拟合了数据；
第三个模型完美拟合了几乎所有的训练数据，但却不能很好的拟合真实的函数，也就是对于不同的训练数据很敏感（高方差，overfitting）。
对于以上第一和第三个模型，我们可以选择模型和超参数来得到效果更好的配置，也就是可以通过验证曲线（validation_curve）来调节。

validation_curve的含义
验证曲线（validation_curve）和学习曲线（sklearn.model_selection.learning_curve()）的区别是，验证曲线的横轴为某个超参数，如一些树形集成学习算法中的max_depth、min_sample_leaf等等。
从验证曲线上可以看到随着超参数设置的改变，模型可能从欠拟合到合适，再到过拟合的过程，进而选择一个合适的位置，来提高模型的性能。
需要注意的是，如果我们使用验证分数来优化超参数，那么该验证分数是有偏差的，它无法再代表魔心的泛化能力，我们就需要使用其他测试集来重新评估模型的泛化能力。
即一般我们需要把一个数据集分成三部分：train、validation和test，我们使用train训练模型，并通过在 validation数据集上的表现不断修改超参数值（例如svm中的C值，gamma值等），当模型超参数在validation数据集上表现最优时，我们再使用全新的测试集test进行测试，以此来衡量模型的泛化能力。
不过有时画出单个超参数与训练分数和验证分数的关系图，有助于观察该模型在该超参数取值时，是否过拟合或欠拟合的情况发生，如下两个图：
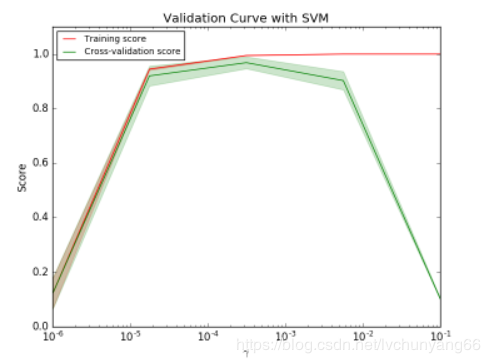
在这里插入图片描述
如图是SVM在不同gamma时，它在训练集和交叉验证上的分数：
gamma很小时，训练分数和验证分数都很低，为欠拟合；
gamma逐渐增加时，两个分数都较高，此时模型相对不错；
gamma太高时，训练分数高，验证分数低，学习器会过拟合。
本例中，可以选验证集准确率开始下降，而测试集越来越高那个转折点作为gamma的最优选择。

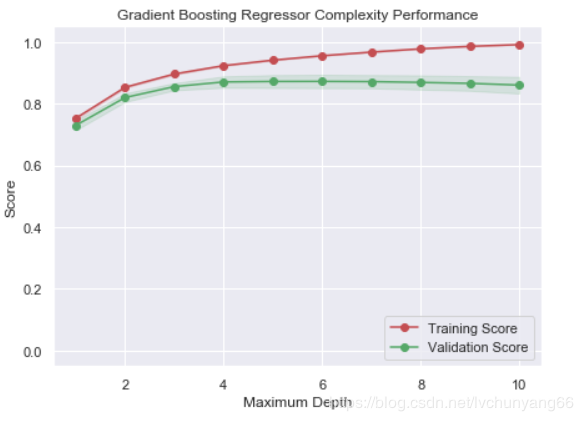
在这里插入图片描述
如上图，max_depth的最佳值应该定位5，code在文末。

validation_curve的试用场景
当拥有大量样本可供使用时，可以将数据分为train、validation、test；当样本数量较少时，可以使用交叉验证，但也一定要留出相同的一部分test数据集，在最后使用。而其余部分假如分成了k fold，就可以循环让k-1 fold做训练集，剩下1个fold做验证集。

validation_curve的使用方法

import numpy as np
import pandas as pd
from time import time
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection  import validation_curve
def ModelComplexity(X, y):
    """ Calculates the performance of the model as model complexity increases.
        The learning and testing errors rates are then plotted. """
    # Create 10 cross-validation sets for training and testing
    cv = ShuffleSplit(n_splits=10,test_size = 0.2, random_state = 0)
    # Vary the max_depth parameter from 1 to 10
    max_depth = np.arange(1,11)
    start = time()
    # Calculate the training and testing scores
    train_scores, test_scores = validation_curve(GradientBoostingRegressor(), X, y, \
        param_name = "max_depth", param_range = max_depth, cv = cv, scoring = 'r2')
    print(time()-start)
    # Find the mean and standard deviation for smoothing
    train_mean = np.mean(train_scores, axis=1)
    train_std = np.std(train_scores, axis=1)
    test_mean = np.mean(test_scores, axis=1)
    test_std = np.std(test_scores, axis=1)
    # Plot the validation curve
    plt.figure(figsize=(7, 5))
    plt.title('Gradient Boosting Regressor Complexity Performance')
    plt.plot(max_depth, train_mean, 'o-', color = 'r', label = 'Training Score')
    plt.plot(max_depth, test_mean, 'o-', color = 'g', label = 'Validation Score')
    plt.fill_between(max_depth, train_mean - train_std, \
        train_mean + train_std, alpha = 0.15, color = 'r')
    plt.fill_between(max_depth, test_mean - test_std, \
        test_mean + test_std, alpha = 0.15, color = 'g')
    # Visual aesthetics
    plt.legend(loc = 'lower right')
    plt.xlabel('Maximum Depth')
    plt.ylabel('Score')
    plt.ylim([-0.05,1.05])
    plt.show()
ModelComplexity(X_train, y_train)

作者：农夫左三拳

超参数参数

1024 个赞