基于MATLAB和Python实现MFCC特征参数提取
1、MFCC概述
在语音识别(Speech Recognition)和话者识别(Speaker Recognition)方面,最常用到的语音特征就是梅尔倒谱系数(Mel-scale FrequencyCepstral Coefficients,简称MFCC)。根据人耳听觉机理的研究发现,人耳对不同频率的声波有不同的听觉敏感度。从200Hz到5000Hz的语音信号对语音的清晰度影响较大。两个响度不等的声音作用于人耳时,则响度较高的频率成分的存在会影响到对响度较低的频率成分的感受,使其变得不易察觉,这种现象称为掩蔽效应。由于频率较低的声音在内耳蜗基底膜上行波传递的距离大于频率较高的声音,故一般来说,低音容易掩蔽高音,而高音掩蔽低音较困难。在低频处的声音掩蔽的临界带宽较高频要小。所以,人们从低频到高频这一段频带内按临界带宽的大小由密到疏安排一组带通滤波器,对输入信号进行滤波。将每个带通滤波器输出的信号能量作为信号的基本特征,对此特征经过进一步处理后就可以作为语音的输入特征。由于这种特征不依赖于信号的性质,对输入信号不做任何的假设和限制,又利用了听觉模型的研究成果。因此,这种参数比基于声道模型的LPCC相比具有更好的鲁邦性,更符合人耳的听觉特性,而且当信噪比降低时仍然具有较好的识别性能。
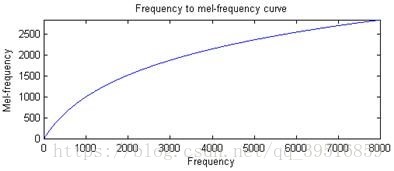
梅尔倒谱系数是在Mel标度频率域提取出来的倒谱参数,Mel标度描述了人耳频率的非线性特性,它与频率的关系可用下式近似表示:
![]()
式中f为频率,单位为Hz。下图为Mel频率与线性频率的关系:
2、 MFCC特征参数提取过程详解

(1)预处理
预处理包括预加重、分帧、加窗函数。
预加重:预加重的目的是提升高频部分,使信号的频谱变得平坦,保持在低频到高频的整个频带中,能用同样的信噪比求频谱。同时,也是为了消除发生过程中声带和嘴唇的效应,来补偿语音信号受到发音系统所抑制的高频部分,也为了突出高频的共振峰。预加重处理其实是将语音信号通过一个高通滤波器:
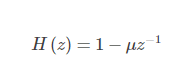
分帧:先将N个采样点集合成一个观测单位,称为帧。通常情况下N的值为256或512,涵盖的时间约为20~30ms左右。为了避免相邻两帧的变化过大,因此会让两相邻帧之间有一段重叠区域,此重叠区域包含了M个取样点,通常M的值约为N的1/2或1/3。通常语音识别所采用语音信号的采样频率为8KHz或16KHz,以8KHz来说,若帧长度为256个采样点,则对应的时间长度是256/8000×1000=32ms。
加窗:将每一帧乘以汉明窗,以增加帧左端和右端的连续性。假设分帧后的信号为S(n), n=0,1…,N-1, N为帧的大小,那么乘上汉明窗
![]()
后 ,W(n)形式如下:
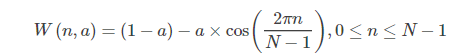
(2)FFT
由于信号在时域上的变换通常很难看出信号的特性,所以通常将它转换为频域上的能量分布来观察,不同的能量分布,就能代表不同语音的特性。所以在乘上汉明窗后,每帧还必须再经过快速傅里叶变换以得到在频谱上的能量分布。对分帧加窗后的各帧信号进行快速傅里叶变换得到各帧的频谱。
(3)谱线能量
对语音信号的频谱取模平方得到语音信号的谱线能量。
(4)计算通过Mel滤波器的能量
将能量谱通过一组Mel尺度的三角形滤波器组,定义一个有M个滤波器的滤波器组(滤波器的个数和临界带的个数相近),采用的滤波器为三角滤波器,中心频率为f(m) 。M通常取22-26。各f(m)之间的间隔随着m值的减小而缩小,随着m值的增大而增宽,如图所示:
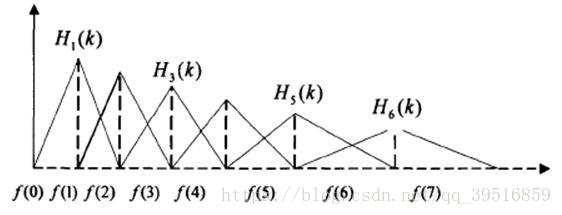
三角滤波器的频率响应定义为:
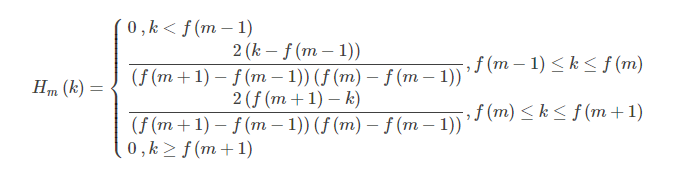
对频谱进行平滑化,并消除谐波的作用,突显原先语音的共振峰。(因此一段语音的音调或音高,是不会呈现在MFCC 参数内,换句话说,以MFCC 为特征的语音辨识系统,并不会受到输入语音的音调不同而有所影响)此外,还可以降低运算量。
计算每个滤波器组输出的对数能量为 :

(5)计算DCT倒谱
经离散余弦变换(DCT)得到MFCC系数 :
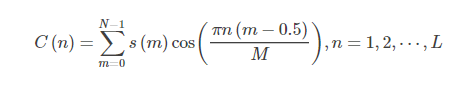
将上述的对数能量带入离散余弦变换,求出L阶的Mel参数。L阶指MFCC系数阶数,通常取12-16。这里M是三角滤波器个数。
3、MATLAB实现方法
注:在提取MFCC参数之前需要加载并使用VOICEBOX工具包
Df=5;
fs=8000;
N=fs/Df;
t=0:1./fs:(N-1)./fs;
x=sin(2*pi*200*t);
bank=melbankm(24,256,8000,0,0.5,'t');%Mel滤波器的阶数为24,fft变换的长度为256,采样频率为8000Hz
%归一化mel滤波器组系数
bank=full(bank);
bank=bank/max(bank(:));
% DCT系数,12*p
for k=1:12
n=0:23;
dctcoef(k,:)=cos((2*n+1)*k*pi/(2*24));
end
%归一化倒谱提升窗口
w=1+6*sin(pi*[1:12]./12);
%w=w/max(w);
%语音信号分帧
xx=enframe(x,256,80);%对x 256点分为一帧
%计算每帧的MFCC参数
for i=1:size(xx,1)
y=xx(i,:);
s=y'.*hamming(256);
t=abs(fft(s));%fft快速傅立叶变换
t=t.^2;
c1=dctcoef*log(bank*t(1:129));
c2=c1.*w';
end
plot(c2);title('MFCC');
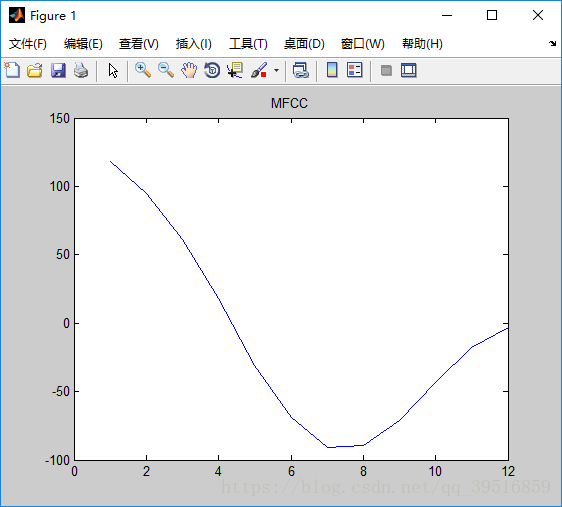
结果:
4、Python实现方法
import numpy as np
from scipy import signal
from scipy.fftpack import dct
import pylab as plt
def enframe(wave_data, nw, inc, winfunc):
'''将音频信号转化为帧。
参数含义:
wave_data:原始音频型号
nw:每一帧的长度(这里指采样点的长度,即采样频率乘以时间间隔)
inc:相邻帧的间隔(同上定义)
'''
wlen=len(wave_data) #信号总长度
if wlen<=nw: #若信号长度小于一个帧的长度,则帧数定义为1
nf=1
else: #否则,计算帧的总长度
nf=int(np.ceil((1.0*wlen-nw+inc)/inc))
pad_length=int((nf-1)*inc+nw) #所有帧加起来总的铺平后的长度
zeros=np.zeros((pad_length-wlen,)) #不够的长度使用0填补,类似于FFT中的扩充数组操作
pad_signal=np.concatenate((wave_data,zeros)) #填补后的信号记为pad_signal
indices=np.tile(np.arange(0,nw),(nf,1))+np.tile(np.arange(0,nf*inc,inc),(nw,1)).T #相当于对所有帧的时间点进行抽取,得到nf*nw长度的矩阵
indices=np.array(indices,dtype=np.int32) #将indices转化为矩阵
frames=pad_signal[indices] #得到帧信号
win=np.tile(winfunc,(nf,1)) #window窗函数,这里默认取1
return frames*win #返回帧信号矩阵
Df=5
fs=8000
N=fs/Df
t = np.arange(0,(N-1)/fs,1/fs)
wave_data=np.sin(2*np.pi*200*t)
#预加重
#b,a = signal.butter(1,1-0.97,'high')
#emphasized_signal = signal.filtfilt(b,a,wave_data)
#归一化倒谱提升窗口
lifts=[]
for n in range(1,13):
lift =1 + 6 * np.sin(np.pi * n / 12)
lifts.append(lift)
#print(lifts)
#分帧、加窗
winfunc = signal.hamming(256)
X=enframe(wave_data, 256, 80, winfunc) #转置的原因是分帧函数enframe的输出矩阵是帧数*帧长
frameNum =X.shape[0] #返回矩阵行数18,获取帧数
#print(frameNum)
for i in range(frameNum):
y=X[i,:]
#fft
yf = np.abs(np.fft.fft(y))
#print(yf.shape)
#谱线能量
yf = yf**2
#梅尔滤波器系数
nfilt = 24
low_freq_mel = 0
NFFT=256
high_freq_mel = (2595 * np.log10(1 + (fs / 2) / 700)) # 把 Hz 变成 Mel
mel_points = np.linspace(low_freq_mel, high_freq_mel, nfilt + 2) # 将梅尔刻度等间隔
hz_points = (700 * (10**(mel_points / 2595) - 1)) # 把 Mel 变成 Hz
bin = np.floor((NFFT + 1) * hz_points / fs)
fbank = np.zeros((nfilt, int(np.floor(NFFT / 2 + 1))))
for m in range(1, nfilt + 1):
f_m_minus = int(bin[m - 1]) # left
f_m = int(bin[m]) # center
f_m_plus = int(bin[m + 1]) # right
for k in range(f_m_minus, f_m):
fbank[m - 1, k] = (k - bin[m - 1]) / (bin[m] - bin[m - 1])
for k in range(f_m, f_m_plus):
fbank[m - 1, k] = (bin[m + 1] - k) / (bin[m + 1] - bin[m])
filter_banks = np.dot(yf[0:129], fbank.T)
filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks) # 数值稳定性
filter_banks = 10 * np.log10(filter_banks) # dB
filter_banks -= (np.mean(filter_banks, axis=0) + 1e-8)
#print(filter_banks)
#DCT系数
num_ceps = 12
c2 = dct(filter_banks, type=2, axis=-1, norm='ortho')[ 1 : (num_ceps + 1)] # Keep 2-13
c2 *= lifts
print(c2)
plt.plot(c2)
plt.show()
结果:
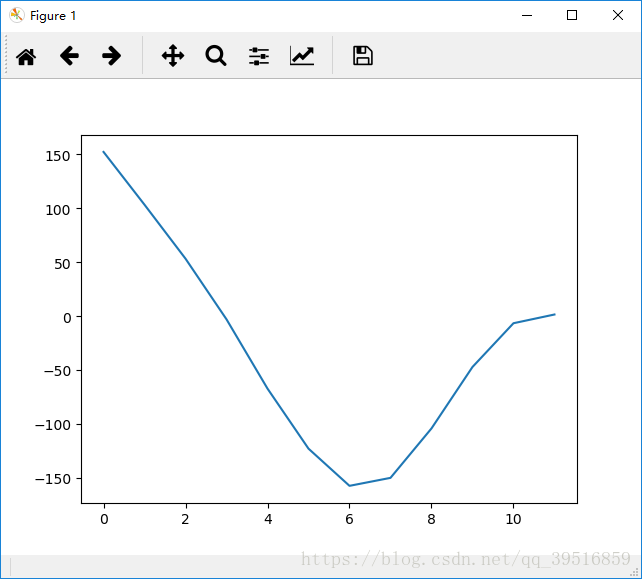
由MATLAB和Python绘制出来的波形可以看出二者计算出来的MFCC倒谱系数的基本走势相同。
参考:http://haythamfayek.com/2016/04/21/speech-processing-for-machine-learning.html
您可能感兴趣的文章:梅尔频率倒谱系数(mfcc)及Python实现对python中Librosa的mfcc步骤详解利用python提取wav文件的mfcc方法对Python使用mfcc的两种方式详解