Python:客运量与货运量预测-BP神经网络
基于Python实现BP神经网络,参考资料会放在最后。
BP神经网络误差向量推导过程用到了微分链式求导
了解整个BP神经网络运行原理之后,就挺简单的
像一般神经网络一样,BP神经网络先进行FP传导即正向传导,案例中只设置了一层隐含层,所以参数层有两层:w1,b1;w2,b2;W参数矩阵的行列:行为输出层的神经元个数,列是输入层的神经元个数。
隐含层的结果:O1=sigmoid(a1)=sigmoid(w1.x.T+b1),隐含层使用了sigmoid激活函数
输出结果:O2=a2=W2*O1+b2 ,最后一层没有用激活函数
损失函数cost=1/2(O2-y)^2 ,括号里面为预测值减实际值得平方,而我们经常使用的误差项err=y-O2,两者的区别,其实err也可以等O2-y,所以err形式决定我们后面的err是否需要加负号,因为cost对O2的偏导数为(O2-y),则err与(O2-y)之间关系换算需要特别注意。
我们这里定义err=y-O2;
损失函数对Wi求偏导即梯度值,求导过程用到微分链式求导
下图可以看到梯度等于误差项 乘以 上一层的输入值,对于最后一层的Wi我们可以得到等于-(y-Oi)Oi-1.T,即-errOi-1.T。最后一层我们没有对a2进行激活函数转换,所以没有激活函数关于a2部分的求导,即O2对a2求导是1,所以忽略.

损失函数对ai进行求偏导则可以得到误差向量,求导过程用到微分链式求导:

这里可以看出不同层误差之间的关系,所以通过误差反向传递,更新wi参数,不断的FP,BP循环,直到MSE达到指定阈值则停止拟合。
下面给出整个项目案例代码,这里说明一点,w1是随机数,所以重新跑一次的时候,MSE学习图会表现的不一样。这里是设置迭代60000次
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
df=pd.read_csv('traffic_data.csv',encoding='GBK')
print(df.head)
x=df[['人口数','机动车数','公路面积']]
y=df[['客运量','货运量']]
print(x)
print(y)
#对数据进行最大最小值归一化
x_scaler=MinMaxScaler(feature_range=(-1,1))
y_scaler=MinMaxScaler(feature_range=(-1,1))
x=x_scaler.fit_transform(x)
y=y_scaler.fit_transform(y)
#对样本进行转置,矩阵运算
sample_in=x.T
sample_out=y.T
#BP神经网络网络参数
max_epochs=60000 #循环迭代次数
learn_rate=0.035 #学习率
mse_final=6.5e-4 #设置一个均方误差的阈值,小于它则停止迭代
sample_number=x.shape[0] #样本数
input_number=x.shape[1] #输入特征数
output_number=y.shape[1] #输出目标个数
hidden_units=8 #隐含层神经元个数
print(sample_number,input_number,output_number)
#定义激活函数Sigmod
# import math
def sigmoid(z):
return 1/(1+np.exp(-z))
def sigmoid_delta(z): #偏导数
return 1/((1+np.exp(-z))**2)*np.exp(-z)
print(sigmoid(0),sigmoid_delta(0))
#一层隐含层
#W1矩阵:M行N列,M等于该层神经元个数,N等于输入特征个数
W1=0.5*np.random.rand(hidden_units,input_number)-0.1
b1=0.5*np.random.rand(hidden_units,1)-0.1
W2=0.5*np.random.rand(output_number,hidden_units)-0.1
b2=0.5*np.random.rand(output_number,1)-0.1
mse_history=[] #空列表,存储迭代的误差
#不设置激活函数
for i in range(max_epochs):
#FP
hidden_out=sigmoid(np.dot(W1,sample_in)+b1) #np.dot矩矩阵相乘,hidden_out1结果为8行20列
network_out=np.dot(W2,hidden_out)+b2 #np.dot矩阵相乘,W2是2行8列,则output结果是2行20列
#误差
err=sample_out-network_out
mse_err=np.average(np.square(err)) #均方误差
mse_history.append(mse_err)
if mse_err<mse_final:
break
#BP
#误差向量
delta2=-err #最后一层的误差
delta1=np.dot(W2.transpose(),delta2)*sigmoid_delta(hidden_out) #前一层的误差向量,这一层对hidden_out用了sigmoid激活函数,要对hidden_out求偏导数;注意最后一步是两个矩阵的点乘,是两个完全相同维度矩阵
#梯度:损失函数的偏导数
delta_W2=np.dot(delta2,hidden_out.transpose())
delta_W1=np.dot(delta1,sample_in.transpose())
delta_b2=np.dot(delta2,np.ones((sample_number,1)))
delta_b1=np.dot(delta1,np.ones((sample_number,1)))
W2-=learn_rate*delta_W2
b2-=learn_rate*delta_b2
W1-=learn_rate*delta_W1
b1-=learn_rate*delta_b1
#损失值画图
print(mse_history)
loss=np.log10(mse_history)
min_mse=min(loss)
plt.plot(loss,label='loss')
plt.plot([0,len(loss)],[min_mse,min_mse],label='min_mse')
plt.xlabel('iteration')
plt.ylabel('MSE loss')
plt.title('Log10 MSE History',fontdict={'fontsize':18,'color':'red'})
plt.legend()
plt.show()
#模型预测输出和实际输出对比图
hidden_out=sigmoid(np.dot(W1,sample_in)+b1)
network_out=np.dot(W2,hidden_out)+b2
#反转获取实际值:
network_out=y_scaler.inverse_transform(network_out.T)
sample_out=y_scaler.inverse_transform(y)
#解决图片中文无法显示
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(8, 6))
plt.plot(network_out[:,0],label='pred')
plt.plot(sample_out[:,0],'r.',label='actual')
plt.title('客运量 ',)
plt.legend()
plt.show()
plt.figure(figsize=(8, 6))
plt.plot(network_out[:,1],label='pred')
plt.plot(sample_out[:,1],'r.',label='actual')
plt.title('货运量 ')
plt.legend()
plt.show()
模拟结果图如下:
这是某一次的迭代结果:
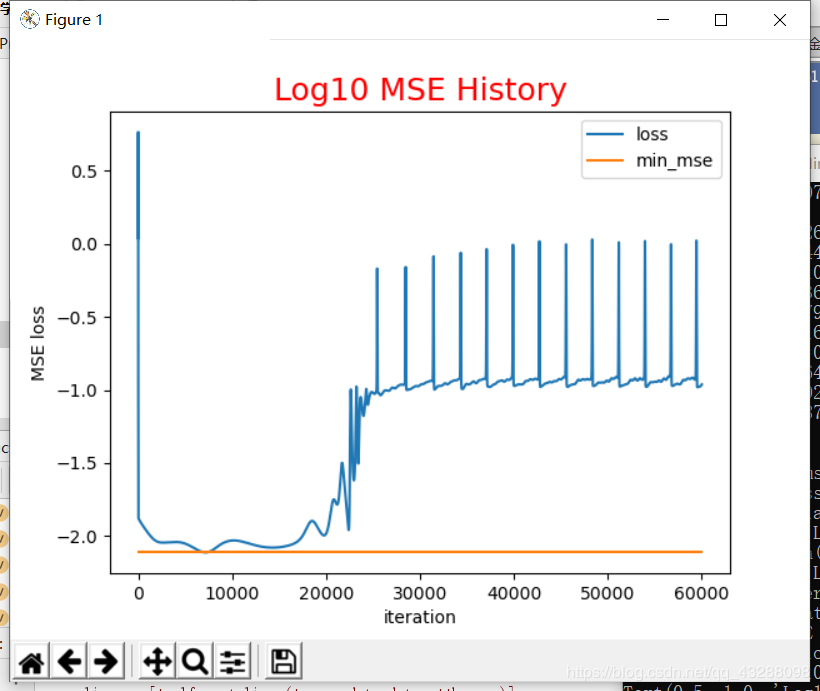
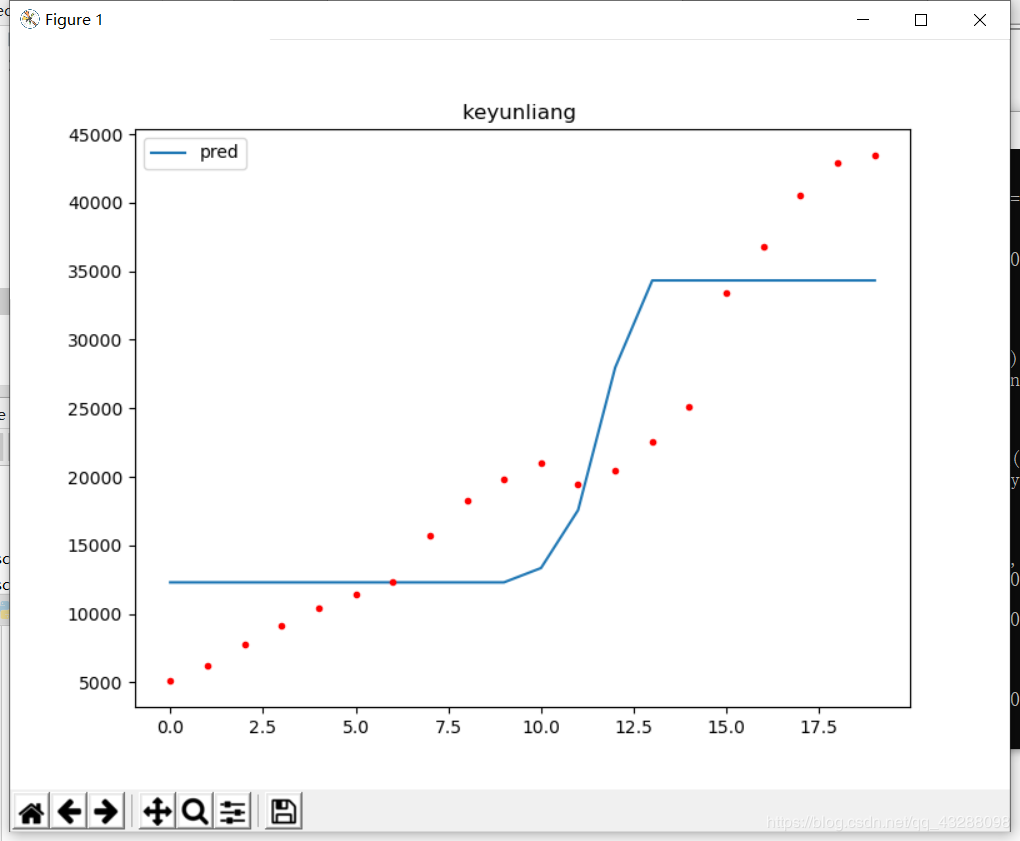
可以看到这个拟合结果不是很好,预测值跟实际值偏差较大
下面给出比较优的模型结果
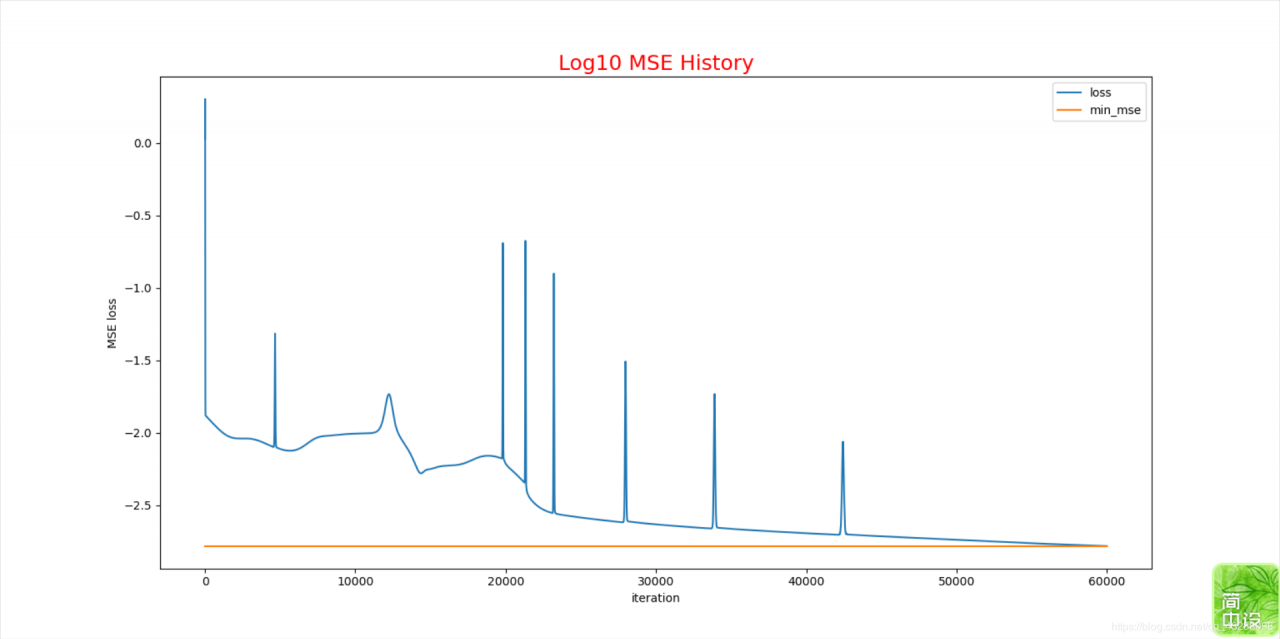
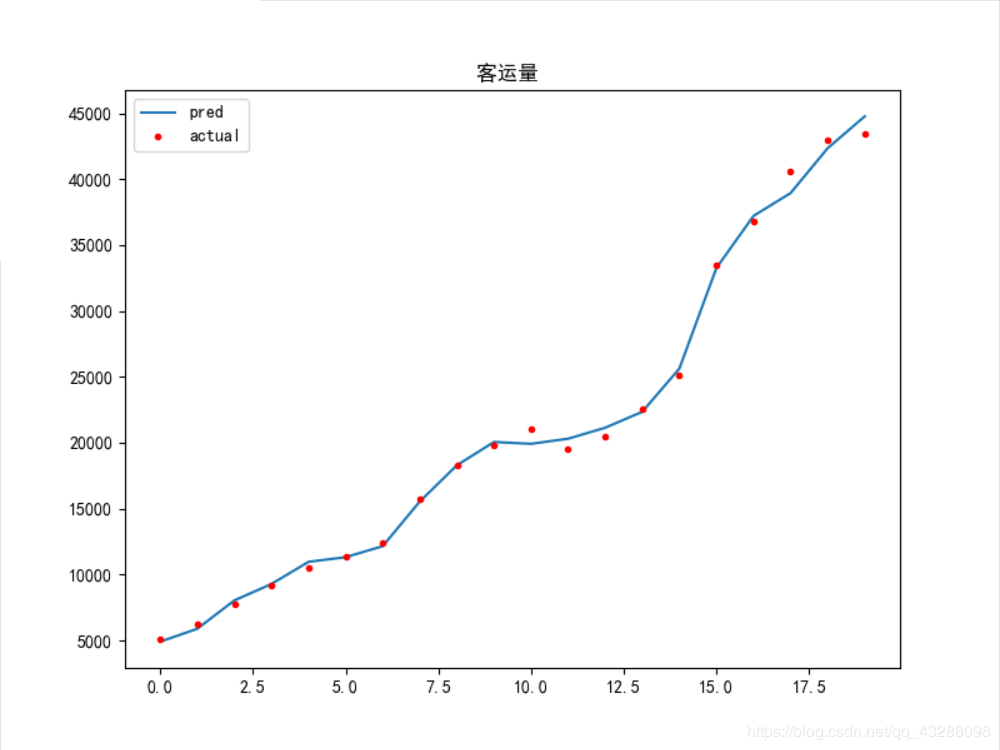
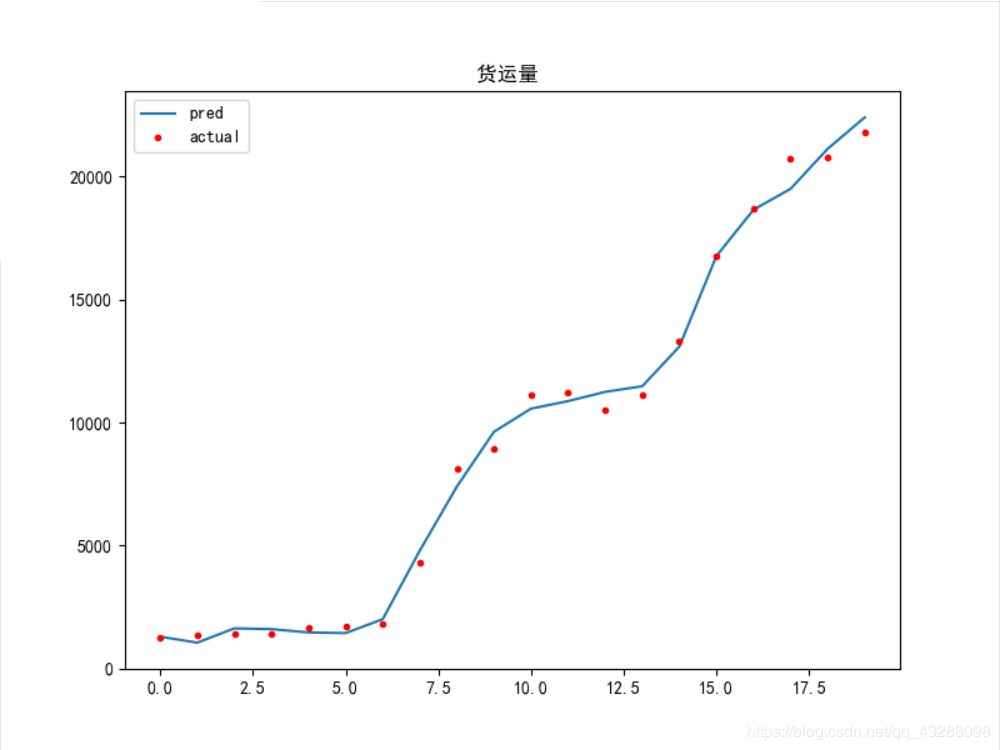
问题:
1.从这里可以看到参数初始值得设定是很重要,解决方法可能就是多训练几次得到一个比较好的模型结果吧
资料:
神经网络,BP算法的理解与推导 https://zhuanlan.zhihu.com/p/45190898 神经网络之BP算法_实战预测案例 https://www.bilibili.com/video/BV1a7411J7SR?t=2522 traffic_data.csv 数据如下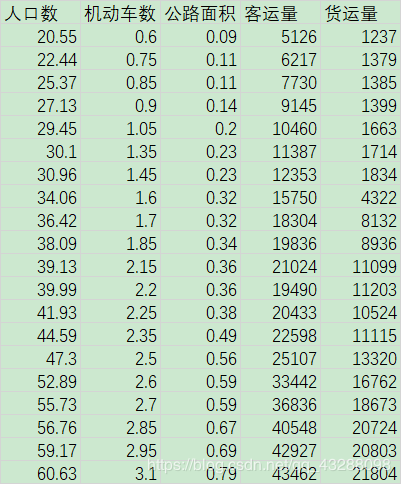
作者:chau.z