BP神经网络实现手写数字输入识别python
代码可以在下面链接中下载:
https://gitee.com/cloud_maple/python_machine_learning.git
训练集和测试集都可以在下面链接中下载:
链接:https://pan.baidu.com/s/1KQuhyM843fEIyeG-87T1QQ
提取码:ln6s
首先,我们需要引入下面两个库
import numpy
import scipy.special
然后创建一个神经网络类,类里有三个函数:初始化函数、训练函数和查询函数。
初始化函数1、引入输入层、隐藏层、输出层的节点个数、学习率这些参数
2、用numpy.random.normal生成初始权重矩阵
(ps1: numpy.random.normal (loc, scale, size) 的作用是生成高斯分布的概率密度随机数,loc是此概率分布的均值(对应着整个分布的中心centre),scale是此概率分布的标准差(对应于分布的宽度,scale越大越矮胖,scale越小,越瘦高), size是输出的shape)
(ps2:pow(x,y) 方法返回 x 的 y 次方的值)
3、定义激活函数,这里用的激活函数是sigmoid函数,下图就是lambda x: scipy.special.expit(x)
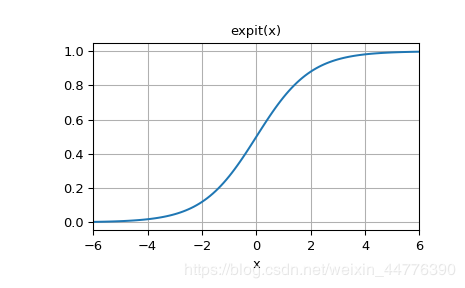
1、numpy.array (object,ndmin) 作用是生成一个数组,ndmin决定生成的最小维数,例子:
>>> np.array([1, 2, 3], ndmin=2)
array([[1, 2, 3]]
2、numpy.dot(x,y)在这里是二维数组的情况下,得到的是两数组的矩阵积,顺序是矩阵x乘以矩阵y
3、更新权重的原理
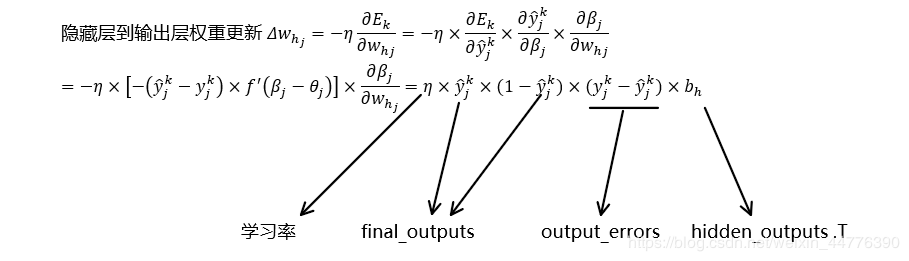
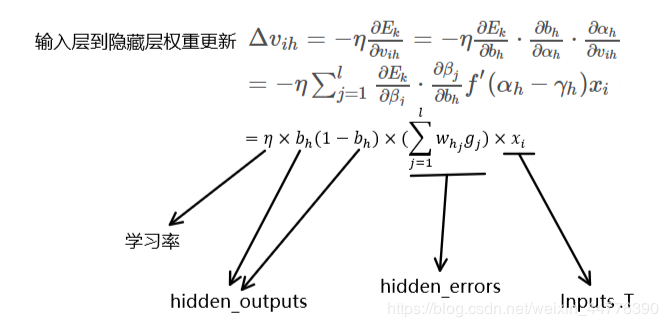
目的就是为了将测试集数据导入已经训练好的神经网络,查询最终的输出,然后与测试集的标签比对,计算准确率。
代码如下:
class NeuralNetwork:
def __init__(self,input_nodes,hidden_nodes,output_nodes,learning_rate):
#初始化输入层、隐藏层、输出层的节点个数、学习率
self.inodes=input_nodes
self.hnodes=hidden_nodes
self.onodes=output_nodes
#定义输入层与隐藏层之间的初始权重参数
self.wih=numpy.random.normal(0.0,pow(self.hnodes,-0.5),(self.hnodes,self.inodes))
#定义隐藏层与输出层之间的初始权重参数
self.who=numpy.random.normal(0.0,pow(self.onodes,-0.5),(self.onodes,self.hnodes))
self.lr=learning_rate
#定义激活函数sigmoid
self.activation_function=lambda x: scipy.special.expit(x)
pass
def train(self,input_list,target_list):
# 输入数据矩阵、目标结果矩阵
inputs=numpy.array(input_list,ndmin=2).T
targets=numpy.array(target_list,ndmin=2).T
# 隐藏层输入
hidden_inputs=numpy.dot(self.wih,inputs)
# 隐藏层激活后输出
hidden_outputs=self.activation_function(hidden_inputs)
# 最终输入
final_inputs=numpy.dot(self.who,hidden_outputs)
# 最终激活后输出
final_outputs=self.activation_function(final_inputs)
#计算误差
output_errors=targets-final_outputs
hidden_errors=numpy.dot(self.who.T,output_errors)
#更新迭代初始权重,公式为权重更新公式,原理为导数、梯度下降。
self.who+=self.lr*numpy.dot((output_errors*final_outputs*(1-final_outputs)),
numpy.transpose(hidden_outputs))
self.wih+=self.lr*numpy.dot((hidden_errors*hidden_outputs*(1-hidden_outputs)),
(numpy.transpose(inputs)))
pass
#查询函数,相当于sklearn中的predict功能,预测新样本的种类
def query(self,inputs_list):
inputs=numpy.array(inputs_list,ndmin=2).T
hidden_inputs=numpy.dot(self.wih,inputs)
hidden_outputs=self.activation_function(hidden_inputs)
final_inputs=numpy.dot(self.who,hidden_outputs)
final_outputs=self.activation_function(final_inputs)
return final_outputs
然后就是数据的导入了
input_nodes =784 #输入层的数量,取决于输入图片(训练和识别)的像素,像素点的数量等于输入层的数量
hidden_nodes =200 #隐藏层的数量,一般比输入层少,但具体不确定,可根据准确率进行调整
output_nodes =10 #输出层的数量,等于需要分类的数量。
learning_rate =0.1 #定义学习率
#用我们的类创建一个神经网络实例
n=NeuralNetwork(input_nodes,hidden_nodes,output_nodes,learning_rate)
训练
这里补充说明一下,为了防止有时候csv储存有误,导致里面有一些奇怪的字符,例如:

例如,这里发生的特殊字符是以UTF-8形式存在的,由于readlines 方法有一个特点就是能将一些特殊字符读取,所以在用split方法会出现’gbk’ codec can’t decode byte 0xbf in position 2: illegal multibyte sequence这种错误。
因此,加入encoding =‘UTF-8’ 以识别这种字符。以后可能还会出现其他形式的特殊字符,因此加入不同的识别由读者们自由取舍。
同时,采用while循环一行行读取。
补充说明:

#=============================训练=======================
#读取数据
training_data_file=open('mnist_train.csv','r',encoding='UTF-8')
training_data = training_data_file.readline()
training_data_list = [training_data]
while training_data_list is not None and training_data_list != '':
if training_data != '':
training_data = training_data_file.readline()
training_data_list.append(training_data)
else:
break
training_data_file.close()
training_data_list.pop(-1)
#训练数据集用于训练的次数
epochs=5
for e in range(epochs):
for record in training_data_list:
#根据逗号,将文本数据进行拆分
all_values=record.split(',')
#将文本字符串转化为实数,并创建这些数字的数组。
inputs=(numpy.asfarray(all_values[1:])/255*0.99+0.01)
#创建用零填充的数组,数组的长度为output_nodes,加0.01解决了0输入造成的问题
targets=numpy.zeros(output_nodes)+0.01
#使用目标标签,将正确元素设置为0.99
targets[int(all_values[0])]=0.99
#导入训练网络更新权重值
n.train(inputs,targets)
pass
pass
这里补充说明一下,CSV格式是逗号分隔数值的存储格式。CSV文件的每一行是一维数据,可以使用Python中的列表类型表示,整个CSV文件是一个二维数据,由表示每一行的列表类型作为元素,成一个二维列表。这里再附一张图帮助理解:

最后就是测试了
#=============================测试=======================
#读取数据
test_data_file=open('test.csv','r',encoding='UTF-8')
test_data = test_data_file.readline()
test_data_list = [test_data]
while test_data_list is not None and test_data_list != '':
if test_data != '':
test_data = test_data_file.readline()
test_data_list.append(test_data)
else:
break
test_data_file.close()
test_data_list.pop(-1)
#通过类方法query输出test数据集中的每一个样本的训练标签和实例标签进行对比。
scorecord=[]
for record in test_data_list:
#根据逗号,将文本数据进行拆分,csv格式是纯文本
all_values=record.split(',')
#获得标签
correct_label=int(all_values[0])
#将文本字符串转化为实数,并创建这些数字的数组。
inputs=(numpy.asfarray(all_values[1:])/255*0.99)+0.01
#导入查询函数获得最终输出
outputs=n.query(inputs)
#转换成标签值
label=numpy.argmax(outputs)
if (label==correct_label):
scorecord.append(1)
else:
scorecord.append(0)
pass
pass
计算准确率
#计算准确率
scorecord_array=numpy.asarray(scorecord)
print("accuracy=",scorecord_array.sum()/scorecord_array.size)
关于不同迭代次数与隐藏层层数对测试集准确率影响的统计
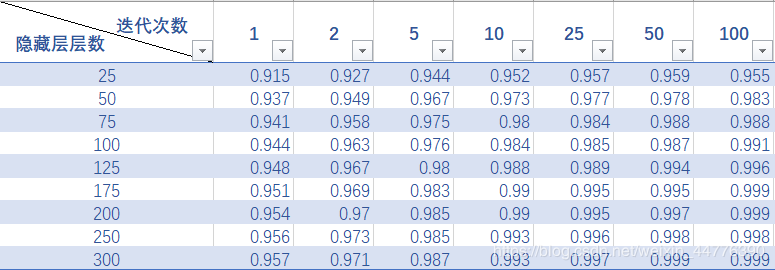
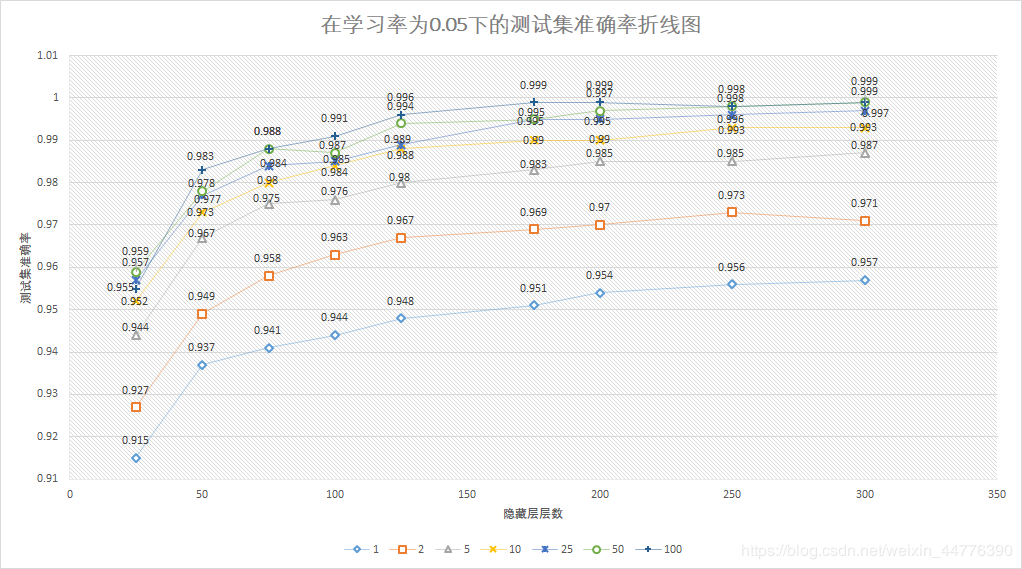
补充说明:训练集数为60000。
(由于实验数据选择了保留3位小数,导致产生了四个最高点,不方便进一步分析优劣,下次会注意保留4-5位小数)
一、关于迭代次数与隐藏层层数
由图中可以看出,在隐藏层层数较少时(图中为25),迭代25、50、100次对准确率波动的影响差别不大,甚至迭代25、50次的准确率还要高过迭代100次。
但是,当隐藏层层数在150到200之间时,迭代次数对准确率的影响显现,直接产生了两个最高点(100,175,0.999)和(100,200,0.999),此时的准确率已经十分接近1了。
而当隐藏层层数达到300时,迭代50次与迭代100次同时产生了最高点,分别为(50,300,0.999)和(100,300,0.999)
二、关于时间
随着迭代次数增加,训练时间会爆炸式增长。粗略计算,当迭代次数为1-2时,训练时间大概在3分钟左右;当迭代次数为5时,训练时间大概在5-10分钟。
而迭代次数上升到50次时,训练时间成了漫长的2小时左右。当迭代次数为100时,训练时间更加夸张,大概在4-5小时左右。
同时,不但迭代次数对训练时间有影响,隐藏层层数的增加对训练时间的增多同样是具有一定的影响的,不过相比迭代次数没这么明显的变化。
三、总结
基于训练时间成本来看,既然(50,300)能达到与(100,175)、(100,200)和(100,300)的测试准确率结果相近,则说明300个隐藏层节点的设置是比较适合60000这个数量的数据集的,能够有效了降低时间成本。
(补充一下,由于时间关系,我没有去测试关于不同学习率对测试准确率的影响,或许学习率会使得低迭代次数,高隐藏层层数的组合的准确率获得一定的提升,但过高的学习率可能适得其反,有兴趣的朋友可以去测试一下)
最后的感想通过上面代码的注释和补充,应该看起来不会那么晦涩难懂了吧,当然最重要的是BP算法的理论掌握,原理一定要掌握。
另外,不要去试着将自己写的手写数字图片放进去测试,它能让你测试到自闭(来自一个钻进图像灰度值转换和图像转CSV的浪费了大量时间的憨憨的忠告),因为它还不够完善,学习能力还不够强,因此它是无法识别自己写的手写数字图片放进去测试的。
作者:学习容易上头