python实现BP神经网络回归预测模型
神经网络模型一般用来做分类,回归预测模型不常见,本文基于一个用来分类的BP神经网络,对它进行修改,实现了一个回归模型,用来做室内定位。模型主要变化是去掉了第三层的非线性转换,或者说把非线性激活函数Sigmoid换成f(x)=x函数。这样做的主要原因是Sigmoid函数的输出范围太小,在0-1之间,而回归模型的输出范围较大。模型修改如下:


代码如下:
#coding: utf8
''''
author: Huangyuliang
'''
import json
import random
import sys
import numpy as np
#### Define the quadratic and cross-entropy cost functions
class CrossEntropyCost(object):
@staticmethod
def fn(a, y):
return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a)))
@staticmethod
def delta(z, a, y):
return (a-y)
#### Main Network class
class Network(object):
def __init__(self, sizes, cost=CrossEntropyCost):
self.num_layers = len(sizes)
self.sizes = sizes
self.default_weight_initializer()
self.cost=cost
def default_weight_initializer(self):
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)/np.sqrt(x)
for x, y in zip(self.sizes[:-1], self.sizes[1:])]
def large_weight_initializer(self):
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(self.sizes[:-1], self.sizes[1:])]
def feedforward(self, a):
"""Return the output of the network if ``a`` is input."""
for b, w in zip(self.biases[:-1], self.weights[:-1]): # 前n-1层
a = sigmoid(np.dot(w, a)+b)
b = self.biases[-1] # 最后一层
w = self.weights[-1]
a = np.dot(w, a)+b
return a
def SGD(self, training_data, epochs, mini_batch_size, eta,
lmbda = 0.0,
evaluation_data=None,
monitor_evaluation_accuracy=False): # 用随机梯度下降算法进行训练
n = len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta, lmbda, len(training_data))
print ("Epoch %s training complete" % j)
if monitor_evaluation_accuracy:
print ("Accuracy on evaluation data: {} / {}".format(self.accuracy(evaluation_data), j))
def update_mini_batch(self, mini_batch, eta, lmbda, n):
"""Update the network's weights and biases by applying gradient
descent using backpropagation to a single mini batch. The
``mini_batch`` is a list of tuples ``(x, y)``, ``eta`` is the
learning rate, ``lmbda`` is the regularization parameter, and
``n`` is the total size of the training data set.
"""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
def backprop(self, x, y):
"""Return a tuple ``(nabla_b, nabla_w)`` representing the
gradient for the cost function C_x. ``nabla_b`` and
``nabla_w`` are layer-by-layer lists of numpy arrays, similar
to ``self.biases`` and ``self.weights``."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = [] # list to store all the z vectors, layer by layer
for b, w in zip(self.biases[:-1], self.weights[:-1]): # 正向传播 前n-1层
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# 最后一层,不用非线性
b = self.biases[-1]
w = self.weights[-1]
z = np.dot(w, activation)+b
zs.append(z)
activation = z
activations.append(activation)
# backward pass 反向传播
delta = (self.cost).delta(zs[-1], activations[-1], y) # 误差 Tj - Oj
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose()) # (Tj - Oj) * O(j-1)
for l in xrange(2, self.num_layers):
z = zs[-l] # w*a + b
sp = sigmoid_prime(z) # z * (1-z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp # z*(1-z)*(Err*w) 隐藏层误差
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) # Errj * Oi
return (nabla_b, nabla_w)
def accuracy(self, data):
results = [(self.feedforward(x), y) for (x, y) in data]
alist=[np.sqrt((x[0][0]-y[0])**2+(x[1][0]-y[1])**2) for (x,y) in results]
return np.mean(alist)
def save(self, filename):
"""Save the neural network to the file ``filename``."""
data = {"sizes": self.sizes,
"weights": [w.tolist() for w in self.weights],
"biases": [b.tolist() for b in self.biases],
"cost": str(self.cost.__name__)}
f = open(filename, "w")
json.dump(data, f)
f.close()
#### Loading a Network
def load(filename):
"""Load a neural network from the file ``filename``. Returns an
instance of Network.
"""
f = open(filename, "r")
data = json.load(f)
f.close()
cost = getattr(sys.modules[__name__], data["cost"])
net = Network(data["sizes"], cost=cost)
net.weights = [np.array(w) for w in data["weights"]]
net.biases = [np.array(b) for b in data["biases"]]
return net
def sigmoid(z):
"""The sigmoid function."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Derivative of the sigmoid function."""
return sigmoid(z)*(1-sigmoid(z))
调用神经网络进行训练并保存参数:
#coding: utf8
import my_datas_loader_1
import network_0
training_data,test_data = my_datas_loader_1.load_data_wrapper()
#### 训练网络,保存训练好的参数
net = network_0.Network([14,100,2],cost = network_0.CrossEntropyCost)
net.large_weight_initializer()
net.SGD(training_data,1000,316,0.005,lmbda =0.1,evaluation_data=test_data,monitor_evaluation_accuracy=True)
filename=r'C:\Users\hyl\Desktop\Second_158\Regression_Model\parameters.txt'
net.save(filename)
第190-199轮训练结果如下:

调用保存好的参数,进行定位预测:
#coding: utf8
import my_datas_loader_1
import network_0
import matplotlib.pyplot as plt
test_data = my_datas_loader_1.load_test_data()
#### 调用训练好的网络,用来进行预测
filename=r'D:\Workspase\Nerual_networks\parameters.txt' ## 文件保存训练好的参数
net = network_0.load(filename) ## 调用参数,形成网络
fig=plt.figure(1)
ax=fig.add_subplot(1,1,1)
ax.axis("equal")
# plt.grid(color='b' , linewidth='0.5' ,linestyle='-') # 添加网格
x=[-0.3,-0.3,-17.1,-17.1,-0.3] ## 这是九楼地形的轮廓
y=[-0.3,26.4,26.4,-0.3,-0.3]
m=[1.5,1.5,-18.9,-18.9,1.5]
n=[-2.1,28.2,28.2,-2.1,-2.1]
ax.plot(x,y,m,n,c='k')
for i in range(len(test_data)):
pre = net.feedforward(test_data[i][0]) # pre 是预测出的坐标
bx=pre[0]
by=pre[1]
ax.scatter(bx,by,s=4,lw=2,marker='.',alpha=1) #散点图
plt.pause(0.001)
plt.show()
定位精度达到了1.5米左右。定位效果如下图所示:
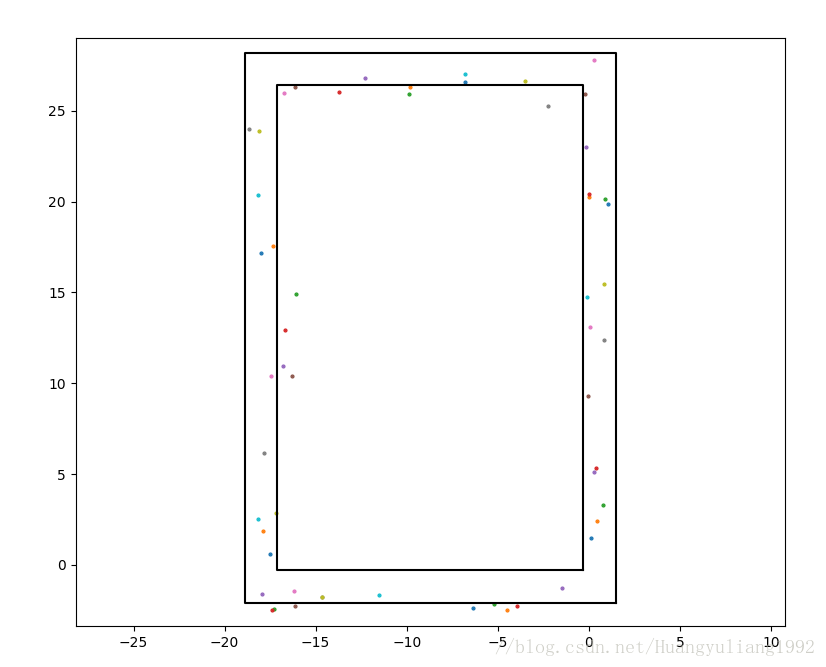
真实路径为行人从原点绕环形走廊一圈。
您可能感兴趣的文章:神经网络(BP)算法Python实现及应用Python实现的三层BP神经网络算法示例Python编程实现的简单神经网络算法示例Python与人工神经网络:使用神经网络识别手写图像介绍TensorFlow平台下Python实现神经网络Python实现的NN神经网络算法完整示例python使用RNN实现文本分类python编写朴素贝叶斯用于文本分类Python使用循环神经网络解决文本分类问题的方法详解