代码in数学（一）：贝塞尔函数 的MATLAB与SciPy对比——中篇

SciPy中的Bessel函数计算

中篇中将处理的基本问题：

1. SciPy和MATLAB文档中Bessel微分方程的不同

2. SciPy中Bessel函数的功能框架及其与MATLAB的对应关系

3. 在物理问题计算中的数据维度问题

4. 微积分计算

下篇中将处理的高阶问题：

5. 球坐标Bessel函数

6. 如何使用Cython加速计算

7. 如何使用numpy避免循环

8. 如何使用并行和GIL技术

1. SciPy和MATLAB文档中Bessel微分方程的不同

非常有必要首先补充一些基本的数学物理知识，Bessel方程是描述各类和波动有关的物理现象的，在数学物理中极其重要。数值计算工具大大降低了使用这个数理工具完成各类本质上是数学求解问题的开发和研究任务，因此，我们有必要了解这些工具如何使用。怎么算了解？我们设立四个指标：

计算准确性

计算效率

适用性

可解释性

所有这些标准的订立和提升，都要求我们在使用计算工具之前，对数学本身和问题本身有深刻和正确的理解与表述。为此，我们首先从两个文档对Bessel方程的表述的不同，讲一讲这个方程的推导过程。

Bessel函数的符号在SciPy的文档里与MATLAB不同，输入/自变量为x，系数ν\nuν写成了α\alphaα，第三项导致符号也不一样：

x2d2ydx2+xdydx+(x2−α2)y=0x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+\left(x^{2}-\alpha^{2}\right) y=0x2dx2d2y​+xdxdy​+(x2−α2)y=0

MATLAB文档中的Bessel函数表达式：

z2d2ydz2+zdydz−(z2+ν2)y=0z^{2} \frac{d^{2} y}{d z^{2}}+z \frac{d y}{d z}-\left(z^{2}+\nu^{2}\right) y=0z2dz2d2y​+zdzdy​−(z2+ν2)y=0

Bessel函数在数学物理中，是Bessel方程的解，复变函数在Bessel微分方程上的应用，使得α\alphaα可以是复数。Bessel微分方程在历史上有两个推导方法，其一是从亥姆霍兹方程导出：

∇2u+k2u=0\nabla^{2} u+k^{2} u=0∇2u+k2u=0

经过曲线坐标变换得到：

1ρ∂∂ρ(ρ∂u∂ρ)+1ρ2∂2u∂ϕ2+∂2u∂z2+k2u=0\frac{1}{\rho} \frac{\partial}{\partial \rho}\left(\rho \frac{\partial u}{\partial \rho}\right)+\frac{1}{\rho^{2}} \frac{\partial^{2} u}{\partial \phi^{2}}+\frac{\partial^{2} u}{\partial z^{2}}+k^{2} u=0ρ1​∂ρ∂​(ρ∂ρ∂u​)+ρ21​∂ϕ2∂2u​+∂z2∂2u​+k2u=0

取u(ρ,ϕ,z)=R(ρ)Φ(ϕ)Z(z)u(\rho, \phi, z)=R(\rho) \Phi(\phi) Z(z)u(ρ,ϕ,z)=R(ρ)Φ(ϕ)Z(z)：

{Φ′′(ϕ)+m2Φ(ϕ)=0Z′′(z)−ω2Z(z)=0ρ2d2Rdρ2+ρdRdρ+[(k2+ω2)ρ2−m2]R=0\left\{\begin{array}{l}{\Phi^{\prime \prime}(\phi)+m^{2} \Phi(\phi)=0} \\ {Z^{\prime \prime}(z)-\omega^{2} Z(z)=0} \\ {\rho^{2} \frac{d^{2} R}{d \rho^{2}}+\rho \frac{d R}{d \rho}+\left[\left(k^{2}+\omega^{2}\right) \rho^{2}-m^{2}\right] R=0}\end{array}\right.⎩⎨⎧​Φ′′(ϕ)+m2Φ(ϕ)=0Z′′(z)−ω2Z(z)=0ρ2dρ2d2R​+ρdρdR​+[(k2+ω2)ρ2−m2]R=0​

使得：

x=(k2+ω2)ρx=\sqrt{\left(k^{2}+\omega^{2}\right)} \rhox=(k2+ω2)​ρ

y(x)=R(ρ)y(x)=R(\rho)y(x)=R(ρ)

可得到Bessel方程：

x2d2ydx2+xdydx+[x2−m2]y=0x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+\left[x^{2}-m^{2}\right] y=0x2dx2d2y​+xdxdy​+[x2−m2]y=0

可见，如果m=αm = \alpham=α，上面这个方程的形式是SciPy文档中所使用的形式。

在数学史上，另外一个推导Bessel微分方程的途径是从Sturm-Liouville（中译：施图姆-刘维尔）方程推导：

ddx[k(x)dydx]−q(x)y+λρ(x)y=0,(a<x<b)\frac{d}{d x}\left[k(x) \frac{d y}{d x}\right]-q(x) y+\lambda \rho(x) y=0, \quad(a<x<b)dxd​[k(x)dxdy​]−q(x)y+λρ(x)y=0,(a<x<b)

取k(x)=x,q(x)=m2x,ρ(x)=xk(x)=x, \quad q(x)=\frac{m^{2}}{x}, \quad \rho(x)=xk(x)=x,q(x)=xm2​,ρ(x)=x，可得参数式Bessel方程：

ddx[xdydx]−m2xy+λxy=0\frac{d}{d x}\left[x \frac{d y}{d x}\right]-\frac{m^{2}}{x} y+\lambda x y=0dxd​[xdxdy​]−xm2​y+λxy=0

在λ=1\lambda = 1λ=1的特殊情况下，得到Bessel方程：

ddx[xdydx]−m2xy+xy=0\frac{d}{d x}\left[x \frac{d y}{d x}\right]-\frac{m^{2}}{x} y+x y=0dxd​[xdxdy​]−xm2​y+xy=0

不难看出，如果让上式中的m=νm = \num=ν，即得到matlab文档中Bessel微分方程的形式。

多说一句，如果在Sturm-Liouville方程中，取k(x)=1−x2,q=0,ρ=1k(x)=1-x^{2}, \quad q=0, \quad \rho=1k(x)=1−x2,q=0,ρ=1，可以得到另外一个非常重要的数理方程，勒让德方程：

ddx[(1−x2)dydx]+λy=0\frac{d}{d x}\left[\left(1-x^{2}\right) \frac{d y}{d x}\right]+\lambda y=0dxd​[(1−x2)dxdy​]+λy=0

它的解即勒让德函数，后续我们还会介绍这一特殊函数，在很多领域也十分重要。

上述两个途径在国内外的主流数学物理相关教材中都有详细介绍，两者都没有什么错误，因为它们的解都是Bessel函数。

还有必要了解一下Gamma函数，因为它是Bessel函数的一个关键构成要素：

Γ(x)=∫0∞e−ttx−1dt(x>0)\Gamma(x)=\int_{0}^{\infty} e^{-t} t^{x-1} d t \quad(x>0)Γ(x)=∫0∞​e−ttx−1dt(x>0)

它有一个有趣的基本性质：

Γ(x+1)=xΓ(x)\Gamma(x+1)=x \Gamma(x)Γ(x+1)=xΓ(x)

在离散数学中，可表示为：

Γ(n+1)=n!\Gamma(n+1)=n !Γ(n+1)=n!

我们在后续还会进一步讲解matlab和SciPy中对它的计算函数。

SciPy中还有一个Jahnke-Emden λ\lambdaλ函数，定义为：

Λv(x)=Γ(v+1)Jv(x)(x/2)v\Lambda_{v}(x)=\Gamma(v+1) \frac{J_{v}(x)}{(x / 2)^{v}}Λv​(x)=Γ(v+1)(x/2)vJv​(x)​

它是由Gamma函数和第一类Bessel函数组合而成。

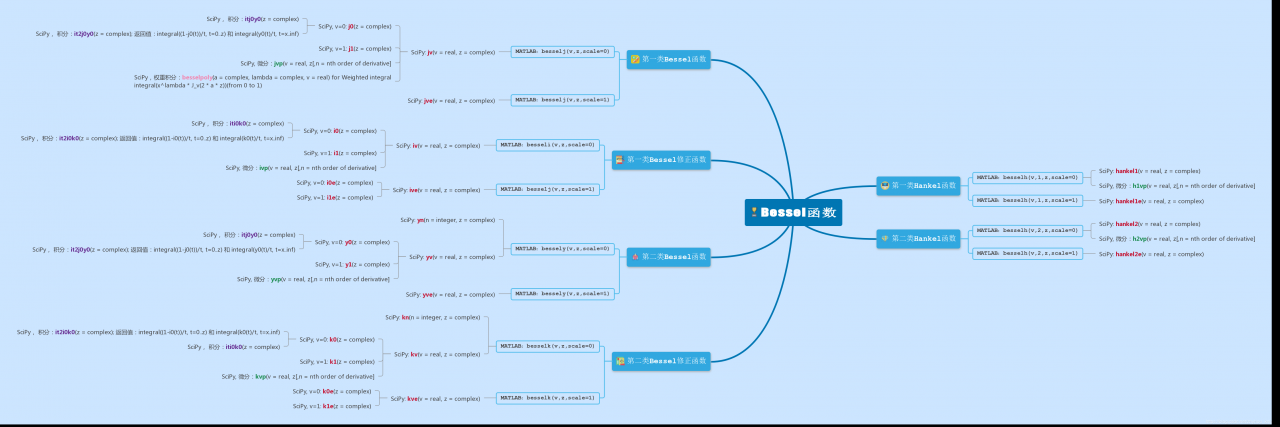
2. SciPy中Bessel函数的功能框架及其与MATLAB的对应关系

SciPy计算Bessel的函数很多，文档中缺乏一个系统框架从整体上把握它们的关联和功能背景介绍。我们从上篇有关MATLAB的Bessel计算函数中，对Bessel函数几个基本问题有了了解：

1）阶数（order）：ν\nuν的影响，ν\nuν可以是整数、实数和复数，复数的情况较少见

2）自变量（input argument or argument for short）：可以是实数，可以是复数

3）积分缩放（scaling）：为避免溢出问题，将输出或因变量的计算结果进行如下缩放，通常缩放因子为1，此时：

第一类Bessel函数的缩放因子： e−abs(imag(Z))e^{-abs(imag(Z))}e−abs(imag(Z))

第一类修正Bessel函数的缩放因子：e−abs(real(Z))e^{-abs(real(Z))}e−abs(real(Z))

第二类Bessel函数的缩放因子： e−abs(imag(Z))e^{-abs(imag(Z))}e−abs(imag(Z))

第二类修正Bessel函数的缩放因子： eZe^ZeZ

第一类Hankel函数的缩放因子：e−iZe^{-i Z}e−iZ

第二类Hankel函数的缩放因子：e+iZe^{+i Z}e+iZ

SciPy是按上述基本问题细化了自己的函数体系，故此，其与MATLAB的对应逻辑如下表所示：

Bessel函数类型	关联	MATLAB函数	SciPy基本函数	关联	SciPy快速计算函数	关联	SciPy积分函数	SciPy微分函数
第一类Bessel函数	无缩放	besselj(v,z)	jv(v,x)	v=0,1	j0(x), j1(x)	v=0	intj0y0(x) int2j0y0(x)	jvp(v,z[,n])
第一类Bessel函数	有缩放	besselj(v,z,1)	jve(v,x)	无	无	无	无	无
第一类Bessel修正函数	无缩放	besseli(v,z)	iv(v,x)	v=0,1	i0(x), i1(x)	v=0	inti0k0(x) int2i0k0(x)	ivp(v,z[,n])
第一类Bessel修正函数	有缩放	besseli(v,z,1)	ive(v,x)	v=0,1	i0e(x), i1e(x)	无	无	无
第二类Bessel函数	无缩放	bessely(v,z)	yv(v=complex,x) yn(n=integer,x)	v=0,1	y0(x), y1(x)	v=0	intj0y0(x) int2j0y0(x)	yvp(v,z[,n])
第二类Bessel函数	有缩放	bessely(v,z,1)	yve(v,x)	无	无	无	无	无
第二类Bessel修正函数	无缩放	bessely(v,z)	kv(v=complex,x) kn(n=integer,x)	v=0,1	k0(x), k1(x)	v=0	inti0k0(x) int2i0k0(x)	kvp(v,z[,n])
第二类Bessel修正函数	有缩放	bessely(v,z,1)	kve(v,x)	v=0,1	k0e(x), k1e(x)	无	无	无
第一类Hankel函数	无缩放	besselh(v,1,z)	hankel1(v,x)	无	无	无	无	h1vp(v,z[,n])
第一类Hankel函数	有缩放	besselh(v,1,z,1)	hankel1e(v,x)	无	无	无	无	无
第二类Hankel函数	无缩放	besselh(v,2,z)	hankel2(v,x)	无	无	无	无	k2vp(v,z[,n])
第二类Hankel函数	有缩放	besseln(v,2,z,1)	hankel2e(v,x)	无	无	无	无	无

Bessel也可以用于权函数，可用于描述类似神经网络结构中权重网络的非线性性质，当然，还有很多其他的应用，SciPy的计算函数为：besselpoly(a,lmb,nu)，其数学表达式为：

∫01xλJν(2ax)dx\int_{0}^{1} x^{\lambda} J_{\nu}(2 a x) d x∫01​xλJν​(2ax)dx

JvJvJv为第一类无缩放Bessel函数。

另有思维导图组织形式，用于说明SciPy中的Bessel函数整合架构。

首先我们对比两者对第一类的计算结果 #Run this in python import numpy as np import scipy from scipy import special x = np.arange(1,11,1) z = special.jv(1,x) print(x,z,sep="\n") % Run this in matlab x = 1:1:10; z = besselj(1,x)

如果是Pycharm，可以在Jupyter或者python console查看、拷贝数据， matlab查看数据的方法更为简单方便。下表对两个函数的计算结果进行了对比，自变量为1到10的整数。

jv in scipy	besselj in matlab	abs difference	relative deviation
0.44005059	0.440050586	4.25507E-09	9.66949E-09
0.57672481	0.576724808	2.24313E-09	3.88942E-09
0.33905896	0.339058959	1.47406E-09	4.34751E-09
-0.06604333	-0.066043328	-1.97645E-09	2.99266E-08
-0.32757914	-0.327579138	-2.40853E-09	7.35253E-09
-0.27668386	-0.276683858	-1.87243E-09	6.76741E-09
-0.00468282	-0.004682823	3.48235E-09	-7.43643E-07
0.23463635	0.234636347	3.14609E-09	1.34083E-08
0.24531179	0.245311787	3.42667E-09	1.39687E-08
0.04347275	0.043472746	3.83114E-09	8.81274E-08

与matlab一样，scipy的bessel计算函数直接接收复数变量

import math import numpy as np import scipy from scipy import special zc = complex(2,4) zc2 = 3-5j jv1 = scipy.special.jv(1,zc) jv2 = scipy.special.jv(1,zc2)

python将计算得到两个复数函数值。
我们再次对两个复数矩阵进行对比，观察两个计算工具的计算精度。

# python import math import numpy as np import scipy from scipy import special stax = -10 stox = 10 stay = -20 stoy = 20 arrayrange = 10 x = np.arange(stax,stox,(stox-stax) / arrayrange) y = np.arange(stay,stoy,(stoy-stay) / arrayrange) z = np.zeros(arrayrange, dtype=complex) for i in range(0,arrayrange): z[i] = complex(x[i],y[i])# z[i]= x[i] + y[i] * 1j jve = scipy.special.jve(1,z) % matlab x = -10:2:10; y = -20:4:20; z = x + 1i*y; jve = besselj(1,z,1)

得到的结果如下表，与上例相同，考虑到应用背景，我们刻意压缩了Scipy计算的精度，但计算结果对比可见，两者在复数域的计算结果也是十分接近的。

besselj(1,z,1) in matlab	jve in scipy
0.0285864494814745 - 0.0780188623704469i	0.02858645+0.07801886j
-0.0922723925185451 + 0.00701986426189972i	-0.09227239-0.00701986j
0.0510447744609186 + 0.0930820963398677i	0.05104477-0.0930821j,
0.0773874093713705 - 0.102334349512687i	0.07738741+0.10233435j
-0.168911332194511 - 0.0422352346166550i	-0.16891133+0.04223523j
0.00000000000000 + 0.00000000000000i	0+0.j
0.168911332194511 + 0.0422352346166550i	0.16891133-0.04223523j
-0.0773874093713705 + 0.102334349512687i	-0.07738741-0.10233435j
-0.0510447744609186 - 0.0930820963398677i	-0.05104477+0.0930821j,
0.0922723925185451 - 0.00701986426189972i	0.09227239+0.00701986j]

3. 在物理问题计算中的数据维度问题

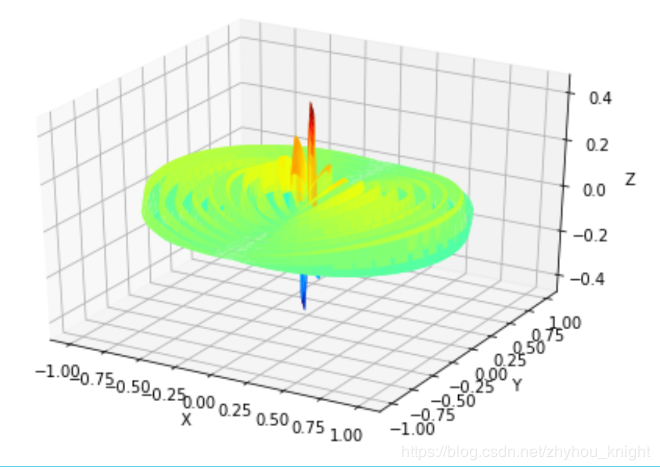
以下我们通过一个具体的绘图代码，观察一下Bessel函数相关的物理问题中数据维度的传递关系。这段代码源于SciPy官网，质量很高，它向我们快捷高效地展示了这样一个通过代码研究物理问题的流程：

第一步：确定坐标系，这决定了数据维度与物理问题的映射关系。本例为笛卡尔坐标，但Bessel方程的解为柱坐标，因此需要坐标变换。

第二步：构建物理问题解的计算函数，计算过程是解析的，或者迭代的。此例比较简单，仅一个解析表达式定义函数，其中，Bessel函数计算得到幅值，与相角相乘得到柱坐标和笛卡尔坐标中z轴的振动幅度数据。

第三步：在计算函数中确定求解域，也就是自变量的取值范围，在物理里，就是要确定什么样的时空范围，具体怎么确定，要具体问题具体分析。本例为振动问题，显然需要找到幅值零点位置，并在其周围选取求解域。

第四步：构建求解域网格矩阵，一定要注意，在物理中，自变量一般是时间和空间，因此，数据的维度要能够映射到时间和空间。

第五步：计算求解得到求解域内的因变量矩阵，这里，最安全的做法，是从物理量（因变量）的矢量表示出发构建其与坐标系对应的数据矩阵。

这就是任何物理问题的数值计算中比较基本的五个要素，不但是绘图显示要用到，能够拥有这种思路，也是任何数值计算中，从实际问题映射到数据的思维和逻辑基本功。以下分析这段代码，演示这一过程：

# Run in python from scipy import * # 用jn_zeros(n,nt)定义计算数据的维度 def BesselinCylinder(n, k, distance, angle): kth_zero = special.jn_zeros(n, k)[-1] print(kth_zero.ndim, kth_zero) #返回k个零点位置，但总是取其中的最大值，调用了50次，打印50次。 return np.cos(angle) * special.jn(n, distance*kth_zero) #计算扫描区域为distance的振动幅度值。 theta = np.r_[0:2*np.pi:50j] #采样数量为50 radius = np.r_[0:1:50j] x = np.array([r * np.cos(theta) for r in radius]) #50*50 y = np.array([r * np.sin(theta) for r in radius]) #50*50 # 计算振动幅度，改变r和k都会有很有趣的变化。 z = np.array([BesselinCylinder(1, 20, r, theta) for r in radius]) import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm fig = plt.figure() ax = Axes3D(fig) ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') plt.show()

为进一步细化坐标映射在整个过程中的核心作用，我们用一段代码说明物理数据映射的一般过程：

第一步，曲线坐标切割，通常是柱坐标、球坐标中的RRR、θ\thetaθ：np.r_[start,stop,stepj]，np.linspace(start,stop,step), np.arange(start,stop,setp) 第二步，如果是二维及二维以上的物理问题，需要构建求解域网格矩阵：meshgrid（R,theta）【e.g., 2D】 第三步，计算完成后，通常要映射到笛卡尔坐标：meshgrid(R * cos(theta), R * sin(theta))【e.g., 2D 】 # 本例无真实物理背景 # This import registers the 3D projection, but is otherwise unused. from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np from scipy import * fig = plt.figure() ax = fig.add_subplot(111, projection='3d') # Create the mesh in polar coordinates and compute corresponding Z. r = np.linspace(0, 1.25, 50) # r坐标切割 p = np.linspace(0, 2*np.pi, 50) # P坐标切割 R, P = np.meshgrid(r, p) # 构建r，P坐标求解域网格矩阵 Z = scipy.special.yv(1,((R**2 - 1)**-2)) #在求解域中计算Z # Express the mesh in the cartesian system. X, Y = R*np.cos(P), R*np.sin(P) # 坐标映射 # Plot the surface. ax.plot_surface(X, Y, Z, cmap=plt.cm.YlGnBu_r) # Tweak the limits and add latex math labels. ax.set_zlim(-1, 0.4) ax.set_xlabel(r'$\phi_\mathrm{real}$') ax.set_ylabel(r'$\phi_\mathrm{im}$') ax.set_zlabel(r'$V(\phi)$') plt.show()

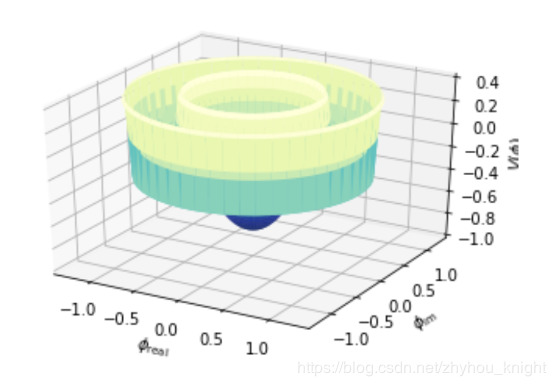
上例中变量的维度如下表：

变量名	物理意义	操作类型	命令	数据维度
r	柱坐标系幅值	坐标切割	np.linspace	{50,}
p	柱坐标系相角	坐标切割	np.linspace	{50,}
R	柱坐标系网格上的幅值矩阵	构建网格矩阵	np.meshgrid	{50,50}
P	柱坐标系网格上的相角矩阵	构建网格矩阵	np.meshgrid	{50,50}
Z	柱坐标系网格上的计算结果	计算得到因变量网格矩阵	特定的计算函数，算法和工作量的核心	{50,50}
X	笛卡尔坐标系网格上的x坐标矩阵	柱坐标网格映射到笛卡尔坐标网格	np.meshgrid	{50,50}
Y	笛卡尔坐标系网格上的x坐标矩阵	柱坐标网格映射到笛卡尔坐标网格	np.meshgrid	{50,50}

其中np.meshgrid命令的逻辑如下图所示：

可形象地表示为下图的坐标映射关系：

还有一种常用的构建方法，可以通过np.mgrid命令完成，以下通过一个实例演示其过程。

平面波的数据格式——一张图，w维度为t，h维度为x，

以沿x方向传播为例，真空中平面波的一般表达式为：

E(t,x)={EX=0,x is free of fieldEy=A×cos(ωt+kx),y is field vibrating dimension with A1 amplitude in codeEz=0z is free of fieldE(t,x) = \begin{cases} E_X=0, & x\text{ is free of field} \\ E_y=A \times cos(\omega t + k x), & y\text{ is field vibrating dimension with A1 amplitude in code}\\ E_z=0 & z\text{ is free of field} \end{cases}E(t,x)=⎩⎪⎨⎪⎧​EX​=0,Ey​=A×cos(ωt+kx),Ez​=0​x is free of fieldy is field vibrating dimension with A1 amplitude in codez is free of field​

f=ω2π,frequency, f1 in codef=\frac{\omega}{2\pi} , \text{frequency, f1 in code}f=2πω​,frequency, f1 in code

λ=k2π,wave length, lambda1 in code\lambda = \frac{k}{2\pi}, \text{wave length, lambda1 in code}λ=2πk​,wave length, lambda1 in code

我们在x、t维度绘制其电场强度的分布如下：

# 构造一个线极化TM平面波的时空矩阵，并绘制任意时空电场强度分布切片 # 场强是矢量，当线偏振条件下，一个平面波的电场强度时空分布即偏振方向的场强，此例中为y方向 omega1 = 10e8 k = 2 * np.pi / 3 f1 = omega1 / 2 * np.pi lambda1 = k / 2 * np.pi A1 = 300 t, x = np.mgrid[slice(0,30 * 1 / f1,0.01 * 30 * 1 / f1), slice(0,30 * lambda1,0.01 * 30 * lambda1)] Ey = A1 * np.cos(omega1 * t + k * x) # 确定场强范围 Ey = Ey[:-1, :-1] levels = MaxNLocator(nbins=15).tick_values(Ey.min(), Ey.max()) cmap = plt.get_cmap('PiYG') norm = BoundaryNorm(levels, ncolors=cmap.N, clip=True) fig, (ax0, ax1) = plt.subplots(nrows=2) im = ax0.pcolormesh(t, x, Ey, cmap=cmap, norm=norm) fig.colorbar(im, ax=ax0) ax0.set_title('pcolormesh with levels') ax0.set(ylabel='Propagation direction, x [m]', xlabel='Time [s]', title='First set of wave') cf = ax1.contourf(t[:-1, :-1] + 0.01 * 3 * 1 / f1 / 2., x[:-1, :-1] + 0.01 * 3 * lambda1 / 2., Ey, levels=levels, cmap=cmap) fig.colorbar(cf, ax=ax1) ax1.set_title('contourf with levels') ax1.set(ylabel='Propagation direction, x [m]', xlabel='Time [s]', title='Second set of wave') fig.tight_layout() plt.show()

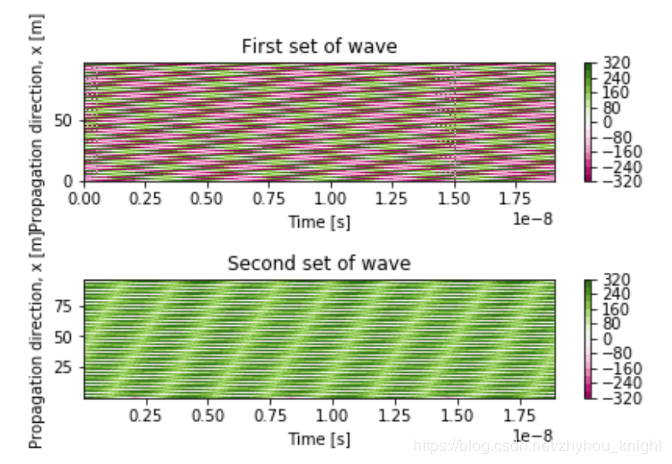
两张图的区别是matplotlib对数据点的处理造成的，可以根据具体情况选择以说明物理问题。以上实例说明np.mgrid也可以通过切片构建时空坐标数据矩阵。但是，mgrid和meshgrid方法的坐标映射关系是相反的，我们可以观察上述代码中mgrid在1:5范围内步长为1切片的网格矩阵输出，以清晰地看到这一点：

TIP:
x,y = np.meshgrid[np.linspace(xstart, xstop, xstep), np.linspace(ystart, ystop, ystep)]
y,x = np.mgrid[slice(ystart, ystop, ystepj), slice(xstart, xtop, xstepj)]
y.x = np.mgrid[ystart:ystop:ystepj, xstart:xtop:xstepj]

4. 微积分操作

接下来，我们通过一段代码讨论Bessel函数微分和积分操作的影响，为方便起见，我们使用上例中没有确切物理背景的代码实例，并主要关注其中的数据转换和提取问题。首先，我们先分析一段代码并观察scipy中0阶bessel积分的效果。

# 本例无真实物理背景 # This import registers the 3D projection, but is otherwise unused. from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np from scipy import * fig = plt.figure() ax = fig.add_subplot(111, projection='3d') # Create the mesh in polar coordinates and compute corresponding Z. r = np.linspace(0, 1.25, 50) # r坐标切割，幅值 p = np.linspace(0, 2*np.pi, 50) # P坐标切割，角度 R, P = np.meshgrid(r, p) # 构建r，P坐标求解域网格矩阵 Z = np.array(scipy.special.itj0y0((R**2 - 1)**-2)).argmax(axis=0) #在求解域中计算零阶第一类和第二类Bessel积分 # Express the mesh in the cartesian system. X, Y = R*np.cos(P), R*np.sin(P) # 坐标映射 # Plot the surface. ax.plot_surface(X, Y, Z, cmap=plt.cm.YlGnBu_r) # Tweak the limits and add latex math labels. ax.set_zlim(-1, 0.4) ax.set_xlabel(r'$\phi_\mathrm{real}$') ax.set_ylabel(r'$\phi_\mathrm{im}$') ax.set_zlabel(r'$V(\phi)$') plt.show()

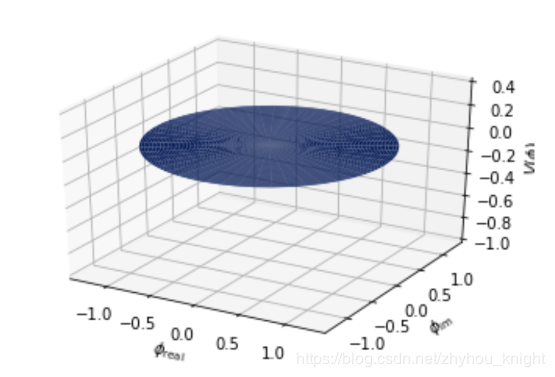
这里有一个技术问题：SciPy中计算Bessel积分只能计算零阶的情况，且是第一类和第二类同时计算，得到两个数组，这两个数组的维度和输入有关，并且同时存储在一个元组里。所以，一般可以进行numpy数组类型转换，然后再进行其他计算和绘图操作。
下表针对上述实例说明取数据的方法：

输入数据维度	积分操作命令	输出数据维度	数据转换和提取函数
ndarray{50,50}	scipy.special.itj0y0(x) it2j0y0 iti0k0 it2i0k0	tuple{2,50,50}	np.array().argmax(axis=0 or 1) axis = 0，取到第一类零阶Bessel函数积分 axis = 1，取到第二类零阶Bessel函数积分

接下来，基于上例，我们观察微分操作的情况，这里我们计算一个零阶第一类Bessel的四阶积分，解析地解决这一问题是十分复杂的。

# 本例无真实物理背景 # This import registers the 3D projection, but is otherwise unused. from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np from scipy import * fig = plt.figure() ax = fig.add_subplot(111, projection='3d') # Create the mesh in polar coordinates and compute corresponding Z. r = np.linspace(0, 1.25, 50) # r坐标切割，幅值 p = np.linspace(0, 2*np.pi, 50) # P坐标切割，角度 R, P = np.meshgrid(r, p) # 构建r，P坐标求解域网格矩阵 Z = scipy.special.jvp(1,((R**2 - 1)**-2),n=4) #在求解域中计算零阶第一类一阶Bessel函数的四阶微分 # Express the mesh in the cartesian system. X, Y = R*np.cos(P), R*np.sin(P) # 坐标映射 # Plot the surface. ax.plot_surface(X, Y, Z, cmap=plt.cm.YlGnBu_r) # Tweak the limits and add latex math labels. ax.set_zlim(-1, 0.4) ax.set_xlabel(r'$\phi_\mathrm{real}$') ax.set_ylabel(r'$\phi_\mathrm{im}$') ax.set_zlabel(r'$V(\phi)$') plt.show()

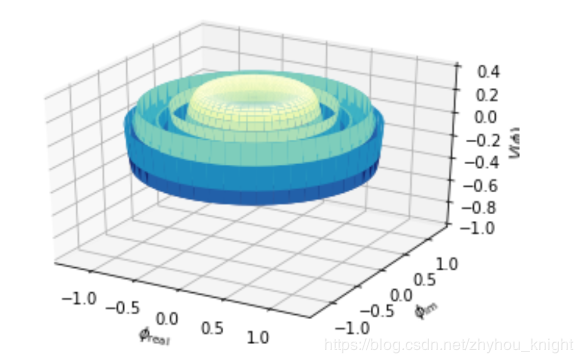
可以看到，这一数学操作并没有产生与基本Bessel函数计算不同的数据类型和维度的变化。

至此，我们已经基本掌握SciPy对Bessel函数计算的主要物理背景、计算问题构建的基本方法流程，以及数据转换、传递和提取的一些基本方法。并且，我们从计算精度上与MATLAB进行了简单对比。更重要的是，我们整理了两个软件工具的函数调用体系与具体数学背景的关系，通过表格、思维导图和具体代码实例，期望提高我们对数学、物理和计算三者间关系的逻辑领会。在此基础上，我们仍然有很多“高端”的问题没有触及：

球坐标Bessel函数 其他特殊类型的Bessel函数 如何使用c加速计算（cython） 如何使用numpy避免低效率的循环，并利用GPU进行矩阵运算 如何使用并行和GIL

但上述问题如果没有具体应用，研究起来不但困难，而且低效。很多同学就是在这个阶段继续阅读文档而变得漫无目的，不但难以评价自己是否真正有所进步，而且很难坚持下去。毕竟SciPy、MATLAB，甚至数学本身，对于物理学家而言，都是工具，而不是目的本身。因此，我们接下来以成像问题为例，开展有关Bessel计算为核心的、具体的、“高端”的SciPy/MATLAB应用讲解，这就构成了下篇的内容。在下篇中，我们就会有的放矢地处理上述这些高阶问题。

作者：远洋海军

IN 函数 scipy matlab 贝塞尔函数 贝塞尔