机器学习(MACHINE LEARNING) 【周志华版-”西瓜书“-笔记】 DAY13-半监督学习
13.1 未标记样本
先说两个概念:
1)有标记样本(Labeled)
训练样本集Dl={(x1,y1), (x2,y2),…, (xl,yl)},这l个样本的类别标记已知。
2)未标记样本(unlabeled)
训练样本集Du={xl+1, x l+2,…, xl+u},u远大于l,这u个样本的类别标记未知。
监督学习技术是基于有标记样本Dl的训练来构建模型,未标记样本Du所包含的信息未被利用;如果有标记样本Dl样例少的话,学得的模型泛化能力也不强,因此需要考虑将未标记样本Du利用起来。利用Du学习模型的方法:
1)主动学习(activelearning)
先用Dl训练出一个模型,然后用这个模型去Du样本中选择一个样本,并和专家进行交互将未标记转变为有标记样本,新标记样本重新训练模型…如此可大幅降低标记成本,只需通过少量未标记样本通过专家来标记就能改善模型,少的查询获得好的性能。
主动学习就是要引入专家知识,通过与外部交互来将部分未标记样本转变为有标记样本。如果不通过外部标记,还可以利用未标记样本,就是半监督学习的研发范围。
2)半监督学习
基于一个事实:未标记样本虽未直接包含标记信息,但若它们与有标记信息样本是从同样的数据源独立同分布采样而来,则它们所包含的关于数据分布的信息对建立模型是有帮助的。
半监督学习 (semi-supervised learning):让学习器不依赖外界交互、自动地利用未标记样本来提升学习性能。在现实任务中,未标记样本多、有标记样本少是一个比价普遍现象,如何利用好未标记样本来提升模型泛化能力,就是半监督学习研究的重点。
要利用未标记样本,需假设未标记样本所揭示的数据分布信息与类别标记存在联系。
一是聚类假设(cluster assumption),假设数据存在簇结构,同一个簇的样本属于同一个类别。另一个是流形假设(manifold assumption),假设数据分布在一个流形结构上,邻近的样本拥有相似的输出值;邻近程度用相似程度来刻画,距离计算大概就是最基础的。
流形假设可看作是聚类假设的推广,不过流形假设对输出值没有限制,比聚类假设的适用范围更广,可用于更多的学习任务。二者的本质是一样的,都基于相似的样本拥有相似的输出这样一个假设。
半监督学习可进一步划分为纯(pure)半监督学习和直推学习(transductive learning):纯半监督学习假定训练数据中的未标记样本并非待预测数据;而直推学习假定学习过程中所考虑的未标记样本恰是待预测数据,学习的目的就是在未标记样本上获得最优泛化性能。
纯半监督学习是基于开放世界的假设,希望学得的模型能适用于训练过程中未观察到的数据;而直推学习是基于封闭世界假设,仅试图对学习过程中观察到的未标记数据进行预测。
13.2 生成式方法
生成式方法(generativemethods)是直接基于生成式模型的方法。该方法假设所有数据(无论是否有标记)都是由同一潜在的模型生成的。通过这个假设通过潜在模型的参数将未标记数据与学习目标联系起来,而未标记数据的标记可作为模型的缺失参数,通常基于EM算法进行极大似然估计求解。生成式方法的重点是对于生成式模型的假设,不同的模型假设将产生不同的方法。当然这个方法的关键也就是这个模型假设必须准确,即假设的生成式模型必须与真实数据分布吻合;否则利用未标记数据反倒会降低泛化性能。该方法简单实现,不过在现实任务中,往往很难事先做出准确的模型假设,除非拥有充分可靠的领域知识。下面通过高斯混合分布模型及EM算法求解来说明生成式半监督学习方法。

 将高斯混合模型换成混合专家模型、朴素贝叶斯模型等即可推导出其他的生成式半监督学习方法。
将高斯混合模型换成混合专家模型、朴素贝叶斯模型等即可推导出其他的生成式半监督学习方法。
13.3 半监督SVM


13.4 图半监督学习
给定一个数据集,将其映射为一个图,数据集中每个样本对应于图中的一个结点,若两个样本之间的相似度很高(或相关性很强),则对应的结点之间存在一条边,边的强度(strength)正比于样本之间的相似度(或相关性)。将有标记样本所对应的结点染色,而未标记样本所对应的结点尚未染色;半监督学习对应于颜色在图上扩散或传播的过程;一个图对应一个矩阵,可基于矩阵运算来进行半监督学习算法的推导与分析。
13.5 基于分歧的方法
与生成式方法、半监督SVM、图半监督学习等基于单学习器利用未标记数据不同,基于分歧的方法(disagreement-basedmethods)使用多学习器,而学习器之间的分歧(disagreement)对未标记数据的利用至关重要。协同训练(co-training)是基于分歧方法的重要代表,针对多视图(multi-view)数据设计,也是多视图学习的代表。
1)多视图数据
多视图数据是指一个数据对象同时拥有多个属性集(attribute set),每个属性集构成一个视图(view)。如一部电影,拥有图像画面信息所对应的属性集、声音信息所对应的属性集、字幕信息所对应的属性集、网上宣传讨论所对应的属性集等多个属性集。若只考虑电影多视图数据中的图像属性集和声音属性集,一个电影片段样本用(,y)表示,其中xi是样本在视图i中的示例,即基于该视图属性描述而得的属性向量。假定x1为图像视图中的属性向量,x2为声音视图中的属性向量;y是标记,如电影类型。
2)相容性
假设不同视图具有相容性(compatibility),即其所包含的关于输出空间y的信息是一致:令y1表示从图像画面信息判别的标记空间,y2表示从声音信息判别的标记空间,则有y=y1=y2。
在相容性的基础上,不同视图信息是互补的,给学习器的构建带来便利。如某个电影片段,从图像上有两人对视,无法判断电影类型,但若加上声音信息中“我爱你”透露的信息,则可判定为电影类型是爱情片。
3)协同训练
协同训练正式基于多视图数据的相容互补性。假设数据拥有两个充分(sufficient)且条件独立视图,充分是指每个视图都包含足以产生最优学习器的信息;条件独立是在给定类别标记条件下每个视图独立。
13.6 半监督聚类
聚类是一种典型的无监督学习任务,然而在现实聚类任务中我们往往能获得一些额外的监督信息,
于是可以通过半监督聚类来利用监督信息以获得更好的聚类效果。
直接上代码
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
test_data = make_blobs(n_samples = 375,n_features = 2,centers = 3,cluster_std = 1)
test_data = test_data[0]
def distanceNorm(Norm,D_value): #距离规范化
# initialization
# Norm for distance
if Norm == '1':
counter = np.absolute(D_value)
counter = np.sum(counter)
elif Norm == '2':
counter = np.power(D_value,2)
counter = np.sum(counter)
counter = np.sqrt(counter)
elif Norm == 'Infinity':
counter = np.absolute(D_value)
counter = np.max(counter)
else:
raise Exception('We will program this later......')
return counter
def chi(x):
if x < 0:
return 1#截距范围内的点的个数
else:
return 0
def fit(features,t,distanceMethod = '2'):
# initialization
labels = list(np.arange(test_data.shape[0]))
distance = np.zeros((len(labels),len(labels))) #初始化计算距离的矩阵
distance_sort = list() #产生一个距离的列表用于距离大小的排列
density = np.zeros(len(labels)) #初始化密度矩阵,一个点对应了一个密度,所以density
#的个数也就是labels的个数,labels 的个数就是样本的个数
distance_higherDensity = np.zeros(len(labels)) #密度比较高的点的初始化矩阵
'''
1.我们首先要计算的是每个点的密度,要计算每个点的密度,首先就要知道截距dc,然后用所有点到该点
的距离值减去这个截距,如果这个减去截距之后结果小于0的点的个数。
2.每个点的密度求出来之后,求出每个点的delta,为每一个点计算Delta距离,该距离的定义是取比该点
局部密度大的所有点的最小距离,如果这个点已经是局部密度最大的点,那么Delta赋值为别的所有点到它
的最大距离。
3.最后,相对应的聚类中心就是相对Delta值比较大的点,如果好几个相近点的Delta值都比较大,
而且比较接近,那么任何一个都可以当作该类的中心
'''
# compute distance 产生距离矩阵
for index_i in range(len(labels)):
for index_j in range(index_i+1,len(labels)):
D_value = features[index_i] - features[index_j]
distance[index_i,index_j] = distanceNorm(distanceMethod,D_value)#距离矩阵中的元素用行纵坐标来索引
distance_sort.append(distance[index_i,index_j])
distance += distance.T
# compute optimal cutoff 选出最优的截距
distance_sort = np.array(distance_sort)
cutoff = distance_sort[int(np.round(len(distance_sort) * t))] #t = 0.02
'''
选择的距离是按照全部距离排序(从小到大排序),然后按照前2%的那个位置所在的距离作为最优截距,
t为什么选择是0.02,这个在其他的文章中是有证明的,此代码中选出的最优截距是经过四舍五入round之后得到的
'''
# computer density 产生密度矩阵
for index_i in range(len(labels)):
distance_cutoff_i = distance[index_i] - cutoff
'''这里的distance[index_i]是将distance矩阵按照行的方式一行一行遍历下来,得到的distance_cutoff_i
是一个包含一整行的行向量,'''
for index_j in range(1,len(labels)):
'''下面的代码的作用就是将上面得到的行向量distance_cutoff_i遍历一遍
如果distance_cutoff_i的值是小于0的,也就是该点在另外一点的规定的截距范围内,截距范围内点的个数就是该
点的密度,这里面密度的个数就是点的个数,就是样本的个数'''
density[index_i] += chi(distance_cutoff_i[index_j])
# search for the max density
Max = np.max(density) # 得到密度最大的点
MaxIndexList = list()
for index_i in range(len(labels)):
if density[index_i] == Max:
MaxIndexList.extend([index_i])
'''遍历所有点的密度,如果某点的密度==最大密度,将改点的索引加入到一个列表中,
这样这个列表中就包含了所有密度最大点的索引index'''
# computer distance_higherDensity
Min = 0
for index_i in range(len(labels)):
'''
遍历所有的点,一单遇到之前存在列表里面的索引(密度最大点的索引),就将索引对应的点于所有点距离的行向量拿出来
也就是距离矩阵中密度最大那几行的航中的值都拿出来,取最大值,就是delta的取值。
delta的取值方式有两种:
1.为每一个点计算Delta距离,该距离的定义是取比该点局部密度大的所有点的最小距离,
2.如果这个点已经是局部密度最大的点,那么Delta赋值为别的所有点到它的最大距离。
下面的if中求delta的方法是第二种方法
'''
if index_i in MaxIndexList:
distance_higherDensity[index_i] = np.max(distance[index_i])
continue
else:
Min = np.max(distance[index_i])
for index_j in range(1,len(labels)):
if density[index_i] < density[index_j] and distance[index_i,index_j] theta:
print(abs(abs(gamma_sorted[i - 1] - gamma_sorted[i]) - abs(gamma_sorted[i] - gamma_sorted[i + 1])))
arr.append(abs(abs(gamma_sorted[i - 1] - gamma_sorted[i]) - abs(gamma_sorted[i] - gamma_sorted[i + 1])))
else:
print('this is abs:',
abs(abs(gamma_sorted[i - 1] - gamma_sorted[i]) - abs(gamma_sorted[i] - gamma_sorted[i + 1])))
arr.append(0)
print('this is arr:',arr)
ap = np.argmax(arr) + 2
print(ap)
print('this is gamma_sorted[ap]:',gamma_sorted[ap - 1],gamma_sorted[ap],gamma_sorted[ap + 1])
plt.figure()
plt.title('GAMMA')
plt.xlabel('x')
plt.ylabel('gamma')
plt.scatter(np.arange(dn),gamma_sorted[:dn],s = 20,c = 'black',alpha = 1)
plt.show()
plt.scatter(np.arange(1,gamma_sorted.shape[0] + 1),gamma_sorted,s = 20,c = 'r',alpha = 1)
plt.show()
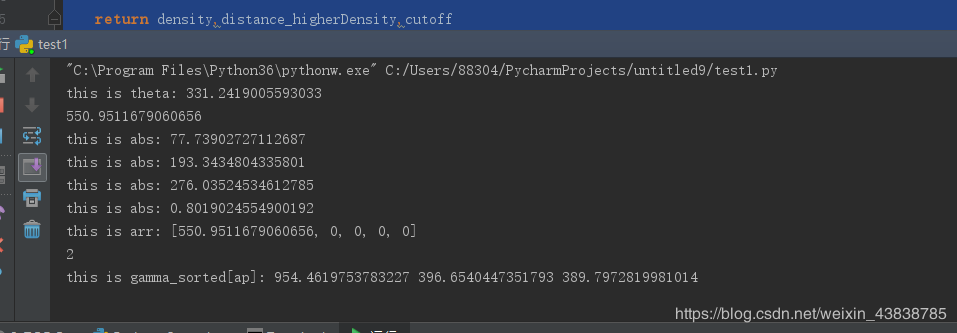
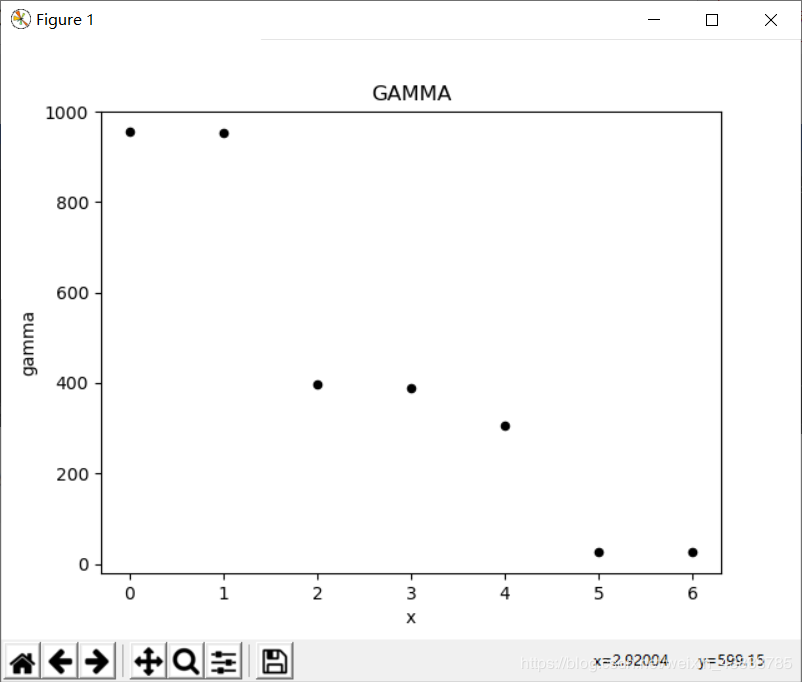
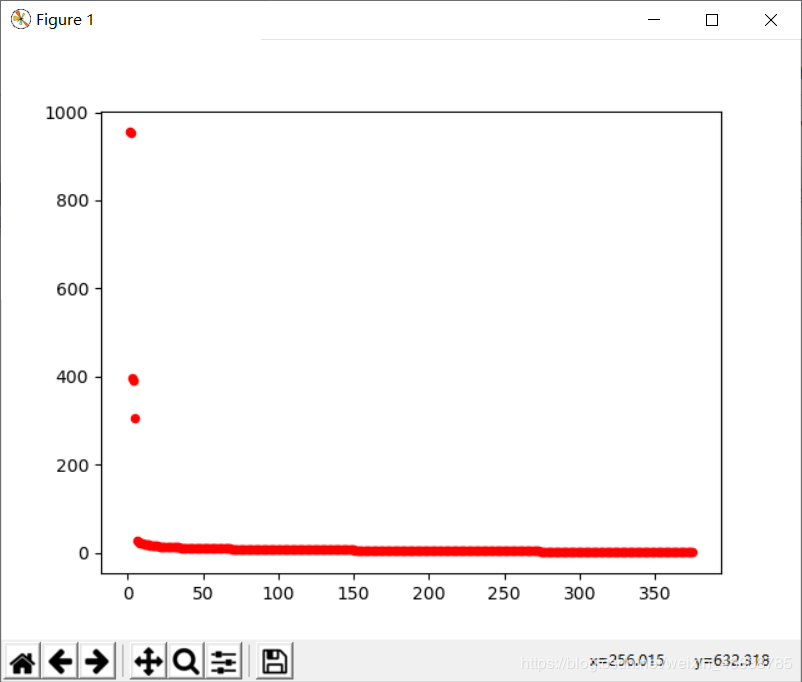
下面是我做的一些结果图,从结果图可以看出,这个算法还是能寻找到一些数据集的聚类中心,但是对有些数据集的聚类中心的自动寻找还是有点困难。

作者:理想007