C语言回溯法解八皇后问题(八皇后算法)
八皇后问题(N皇后问题)的回溯法求解
一、问题描述
在一个国际象棋棋盘上放置八个皇后,使得任何两个皇后之间不相互攻击,求出所有的布棋方法,并推广到N皇后情况。
二、参考资料啥文字都不用看,B站上有个非常详细的动画视频解说,上链接!!!
Click Here!
三、源代码
#include<iostream>
#include<vector>
#include<string>
using namespace std;
void put_queen(int x, int y, vector<vector<int>>&attack)
{//实现在(x,y)放置皇后,对attack数组更新,xy表示放置皇后的坐标,attack表示是否可以放置皇后
//方向数组,方便后面对8个方向进行标记
static const int dx[] = { -1,-1,-1,0,0,1,1,1 };
static const int dy[] = { -1,0,1,-1,1,-1,0,1 };
attack[x][y] = 1;//将皇后位置标记为1
//通过两层for循环,将该皇后可能攻击到的位置标记
for (int i = 1; i < attack.size(); i++)//从皇后位置向1到n-1个距离延伸
{
for (int j = 0; j < 8; j++)//遍历8个方向
{
int nx = x + i * dx[j];//生成的新位置行
int ny = y + i * dy[j];//生成的新位置列
//在棋盘范围内
if (nx >= 0 && nx < attack.size() && ny >= 0 && ny < attack.size())
attack[nx][ny] = 1;//标记为1
}
}
}
//回溯算法
//k表示当前处理的行
//n表示n皇后问题
//queen存储皇后的位置
//attack标记皇后的攻击范围
//solve存储N皇后的全部解法
void backtrack(int k, int n, vector<string>& queen,
vector<vector<int>>& attack,
vector<vector<string>>& solve)
{
if (k == n)//找到一组解
{
solve.push_back(queen);//将结果queen存储至solve
return;
}
//遍历0至n-1列,在循环中,回溯试探皇后可放置的位置
for (int i = 0; i < n; i++)
{
if (attack[k][i] == 0)//判断当前k行第i列是否可以放置皇后
{
vector<vector<int>> tmp = attack;//备份attack数组
queen[k][i] = 'Q';//标记该位置为Q
put_queen(k, i, attack);//更新attack数组
backtrack(k + 1, n, queen, attack, solve);//递归试探k+1行的皇后的位置
attack = tmp;//恢复attack数组
queen[k][i] = '.';//恢复queen数组
}
}
}
vector<vector<string>>solveNQueens(int n)
{//string存储具体的摆放位置,<vector<string>>存放一种解法,二维vector存放全部解法
vector<vector<string>>solve;//存储最后结果
vector<vector<int>>attack;//标记皇后的攻击位
vector<string>queen;//保存皇后位置
//使用循环初始化attack和queen数组
for (int i = 0; i < n; i++)
{
attack.push_back((vector<int>()));
for (int j = 0; j < n; j++)
{
attack[i].push_back(0);
}
queen.push_back("");
queen[i].append(n, '.');
}
backtrack(0, n, queen, attack, solve);
return solve;//返回结果数组
}
int main()
{
//int num;
//cin >> num;//输入皇后数
初始化attack数组
//vector<vector<int>> attack(num,vector<int>(num, 0));
初始化queen数组
//string s;
//for (int i = 0; i < num; i++)s += '.';
//vector<string> queen(num, s);
int n;
cin >> n;
vector<vector<string>>result;
result = solveNQueens(n);
cout << n << "皇后共有" << result.size() << "种解法" << endl;
for (int i = 0; i < result.size(); i++)
{
cout << "解法" << i + 1 << ":" << endl;
for (int j = 0; j < result[i].size(); j++)
{
cout << result[i][j] << endl;
}
cout << endl;
}
system("pause");
return 0;
}
四、测试结果
四皇后
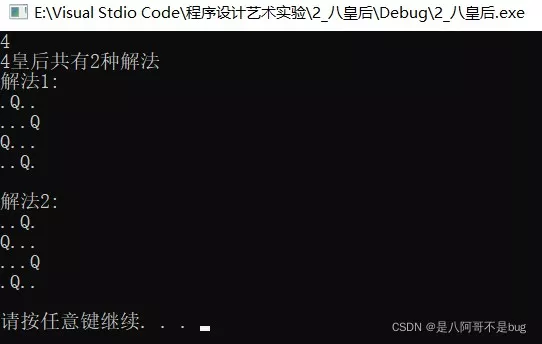
八皇后
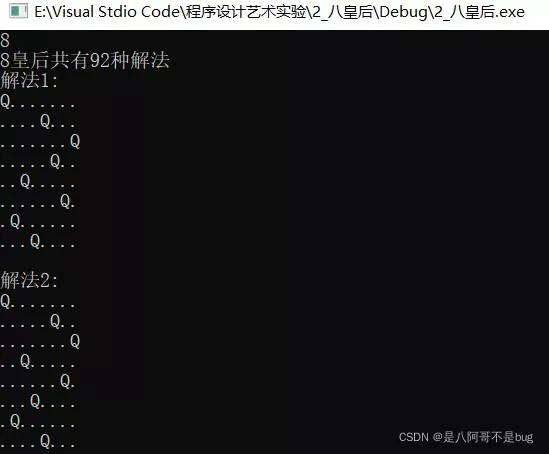
到此这篇关于C语言回溯法解八皇后问题的文章就介绍到这了。希望对大家的学习有所帮助,也希望大家多多支持软件开发网。
相关文章
Serafina
2021-03-06
Michelle
2021-06-24
Jacuqeline
2023-07-20
Galatea
2023-07-20
Qamar
2023-07-20
Nancy
2023-07-20
Paula
2023-07-20
Maren
2023-07-20
Lani
2023-07-20
Viveka
2023-07-20
Radinka
2023-07-20
Rayna
2023-07-20
Edda
2023-07-20
Vevina
2023-07-20
Tertia
2023-07-21
Crystal
2023-07-21
Ianthe
2023-07-21
Raissa
2023-07-21